codeforces round#524 D - Olya and magical square /// 大概算是数学规律题？

题目大意：

t 个测试用例  (1≤t≤103)

给定n k  (1≤n≤10^9,1≤k≤10^18)

表示有一个边长为2^n的正方形格子 每次操作只能将一个格子切割为左上左下右上右下的四等分格子

问进行k次四等分切割后 能否使得 左下角的格子的边长 和 右上角的格子的边长 相等

并且存在一条左下角格子到右上角格子的路径上 经过的格子的边长 也和它们相等

若可以输出 “YES 切割后的log2(边长)” 若操作次数用不完输出“NO”

首先

对边长为2^1的格子四等分切割为1*1小格需要         1          次操作

对边长为2^2的格子四等分切割为1*1小格需要   1*4+1=5   次操作

对边长为2^3的格子四等分切割为1*1小格需要  5*4+1=21  次操作

......op[ i ] = op[ i-1 ] * 4 + 1

由此可预处理出边长为 2^i 的格子切割为1*1小格 需要 op[i] 次操作

然后我们可以发现当切割边长为2^31的格子时 op[31] 即操作次数超出了k的范围10^18

（k最大时不足以将一个2^31边长的格子切为1*1小格）

假设 边长为2^32时 先进行一次操作(分为四格2^31) 剩k-1次操作

之后只对右下的2^31的一格切割 那么k-1次操作绝对能用完

所以路径由左下经左上到右上 经过的三格的边长一样都是2^31 即输出log2(2^31)=31

以此类推 >31 的情况 只要这么处理 答案就是 n-1

n<=31时 ​考虑只切我们要走的路径的格子（假设我们走左边和上边的边缘圈的格子）

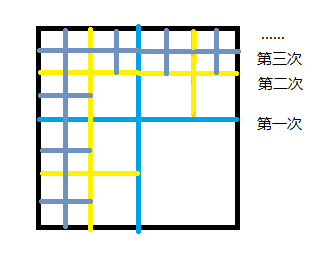
每次只对边缘圈的格子切割一次

第一次需要切割 1 格 (即切1次) (路径格子边长减为 2^(n-1) )

第二次需要切割 3 格 (即切3次) (路径格子边长减为 2^(n-2) )

第三次需要切割 7 格 (即切7次) (路径格子边长减为 2^(n-3) )

......

每次递推可得到下次需要切割的格子数 now(下次) = now(本次) * 2 + 1

累加得到边缘圈应切割次数 tot += now

但是仅仅只切割外围 k次操作很可能还是用不完的

那么此时我们考虑每次切割后不会成为外围圈的格子

因为它们不会影响到我们要走的路径 所以可以直接把它们切成1*1的小格

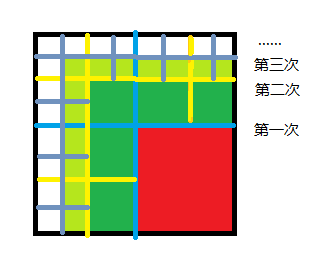
第一次红色格子可切割 共需切割次数 op[ n-1 ] * (3-2)

第二次绿色格子可切割 共需切割次数 op[ n-2 ] * (7-2)

第三次青色格子可切割 共需切割次数 op[ n-3 ] * (15-2)

.....（由于恰好对应下次切割要切割的外围圈格子往内的一圈 往内一圈会少两格 所以恰好是 now(下次)-2 格）

累加得到额外可切割次数 re

那么当只切外围圈的操作数 tot >= k 时 可得到答案

或者 当切外围也切内圈 tot+re>=k 时 也可得到答案

否则 k次操作 就不可能被用完

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k,op[];
int main(){
    for(int i=;i<=;i++) op[i]=op[i-]*4LL+1LL;
    int t; scanf("%d",&t);
    while(t--){
        scanf("%I64d%I64d",&n,&k);
        if(n>) {
            printf("YES %I64d\n",n-);
            continue;
        }
        ll tot=,now=,j=,re=;
        while(now+tot<=k&&j<n){
            tot+=now;
            now=now*+; // now更新为下轮操作需要操作的边缘圈的格数
            j++; // 对边缘圈的小格各操作一次 那么每格的边长又小了一半 即由2^(n-j)变为2^(n-(j+1))
            re+=op[n-j]*(now-);
        }
        if(k>tot+re) printf("NO\n"); // 全部切到1*1小格的操作次数tot+re 仍然不够k次
        else printf("YES %I64d\n",n-j); // n-j 即缩小到最后的 log2(边长)
    }
    return ;
}