Leetcode963. Minimum Area Rectangle II最小面积矩形2

给定在 xy 平面上的一组点，确定由这些点组成的任何矩形的最小面积，其中矩形的边不一定平行于 x 轴和 y 轴。

如果没有任何矩形，就返回 0。

示例 1：

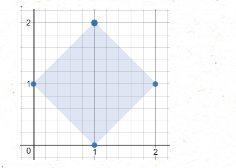
输入：[[1,2],[2,1],[1,0],[0,1]] 输出：2.00000 解释：最小面积的矩形出现在 [1,2],[2,1],[1,0],[0,1] 处，面积为 2。

示例 2：

输入：[[0,1],[2,1],[1,1],[1,0],[2,0]] 输出：1.00000 解释：最小面积的矩形出现在 [1,0],[1,1],[2,1],[2,0] 处，面积为 1。

示例 3：

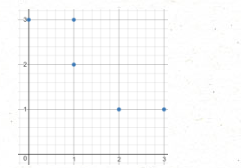
输入：[[0,3],[1,2],[3,1],[1,3],[2,1]] 输出：0 解释：没法从这些点中组成任何矩形。

示例 4：

输入：[[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]] 输出：2.00000 解释：最小面积的矩形出现在 [2,1],[2,3],[3,3],[3,1] 处，面积为 2。

提示：

1. 1 <= points.length <= 50
2. 0 <= points[i][0] <= 40000
3. 0 <= points[i][1] <= 40000
4. 所有的点都是不同的。
5. 与真实值误差不超过 10^-5 的答案将视为正确结果。

该题有很多需要注意的地方。

首先注意题目说的是矩形，而不是正方形。

然后 注意返回值是double型，所以我们要在题中使用double类型。

double类型是靠精度来比较的，而不是 ==

矩形的特征就是：对角线相等且平分

用其他方法要注意题中3个点在一条直线上的情况

这种多重循环的题，比如该题一般来说是n*n*n*n，我们可以优化成n*n*n。

const double esp = 1e-7;
class Solution {
 public:
	 double minAreaFreeRect(vector<vector<int>>& points)
	 {
		 int len = points.size();
		 if (len < 4)
			 return 0;
		 double ans = -1;
         map<pair<double, double>, bool> check;
         for(int i = 0; i < len; i++)
         {
            check[make_pair(points[i][0], points[i][1])] = true;
         }

		 for (int i = 0; i < len; i++)
		 {
             double x1 = points[i][0], y1 = points[i][1];
			 for (int j = 0; j < len; j++)
			 {
                 if(i == j)
                    continue;
                double x2 = points[j][0], y2 = points[j][1];
				for (int k = 0; k < len; k++)
				{
                    if(k == i || k == j)
                        continue;
                    double x3 = points[k][0], y3 = points[k][1];
                    double dis = GetDis(x1, y1, x2, y2);
//中点
                    double midx = (x1 + x2) * 1.0 / 2;
                    double midy = (y1 + y2) * 1.0 / 2;
                    if(abs(dis - GetDis(midx, midy, x3, y3) * 2) < esp)
                    {
                        double x4 = 2 * midx - x3;
                        double y4 = 2 * midy - y3;
                        if(check[make_pair(x4, y4)] == true)
                        {
                            double l = GetDis(x1, y1, x3, y3);
                            double w = GetDis(x1, y1, x4, y4);
                            double area = l * w;
                            ans = ans < 0? area : min(area, ans);
                        }
                    }
                }
             }
         }
         return ans < 0? 0 : ans;
     }
//求距离
     double GetDis(double x1, double y1, double x2, double y2)
     {
         return sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
     }
 };