【证明与推广与背诵】Matrix Tree定理和一些推广

【背诵手记】Matrix Tree定理和一些推广

结论

对于一个无向图\(G=(V,E)\)，暂时钦定他是简单图，定义以下矩阵：

• (入)度数矩阵\(D\),其中\(D_{ii}=deg_i\)。其他=0
• 邻接矩阵\(A\),其中\(A_{ij}=[\exist e=(i,j)]\)。其他=0 (*******wait!*******)
• 关联矩阵\(B\)，其中\(B_{ij}=[\exist e_i=(a,b)](-1)^{[a>b]}\)。其他=0(后面会用到)
• 拉普拉斯矩阵\(L=D-A\)

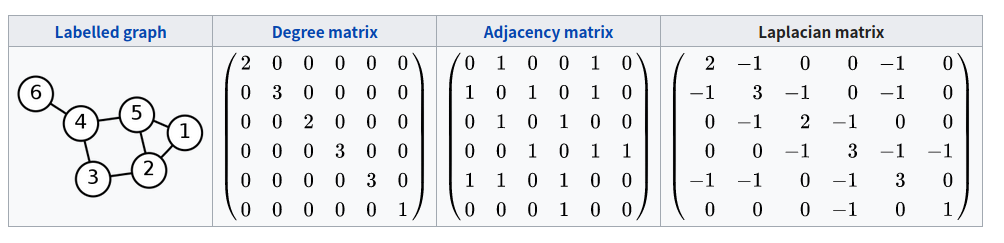
那么，这个图的生成树个数是\(L\)矩阵的任意一个n-1阶主子式的绝对值。

证明

关于拉普拉斯矩阵的性质

• 拉普拉斯矩阵所有的代数余子式值相同

  证明:

  一个显然的事实是拉普拉斯矩阵任何一行/列的元素和\(=0\)

  我将证明一行内代数余子式\(R_{ij}=R_{ik}\)

  先只看对应位置的余子式，可以发现他们的不同在于一个有第\(j\)列没有第\(k\)列，另一个相反。

  根据之前发现的简单的事实\(L_{ik}+L_{ij}+\text{others}=0\) 。我们对于\(C'_{ik}\)，其他列直接乘\(-1\)加到第\(k\)列对应列，此时第\(k\)列对应列就变成了 \(C_{ij}\)的第一列。

  然后考虑把这两个余子式特殊的那一列(j,k)，列交换(用冒泡排序的方法，因为我们不能破坏其他列的相对关系)到第一列，每次交换是要乘上一个-1的，所以最终交换完成后，有一个类似\((-1)^{?}\)的系数。此时除了符号，两个行列式相等了。

  两个余子式都要乘上\((-1)^{?}\)，而这里的系数正好就可以对应上代数余子式需要乘上的\((-1)^{i+j}\)。

  行内检验无异，列就自然成立，稍微推广QED，由上可知自闭证毕

• 拉普拉斯矩阵的行列式的值\(=0\)

  根据行列式按_展开法则证明显然

• 记\(R=R_{11}\)，来证明它一些性质

  • \(|R|=0\)时当且仅当这个图不连通

    证明:

    通过交换行列将联通块排在一起，此时的行列式的值是原来的\((-1)^?\)倍，此时整个矩阵变成了这样:
    \[
    L=\begin{pmatrix}
    L_1 &O&...\\
    O&L_2&...\\
    ...&...&...
    \end{pmatrix}
    \]
    根据拉普拉斯矩阵性质\(|L_i|=0\)以及R的定义可知\(|R|=0\)。

  • \(||R||=1\)当且仅当\(G\)是一棵树

    证明:

    我暂时不会

    循环证明:

    显然一棵树的生成树只有一颗

---

重要补充:
\[
B^TB=L
\]

显然，\(B^TB\)相当于\(B\)中选两列\(e_i,e_j\)列向量然后一个转置后再乘起来，可以验证\(L_{ij}=e_i^Te_j\)。

---

重要补充:

柯西-比内公式(CB)

对于矩阵\(A[n][m]\)和\(B[m][n]\)有:
\[
\det(AB)=\sum_{|S|=n,S\subseteq\{1\dots m\}}\det\left(A_{\{1...n\},S}\right)\det\left(B_{S,\{1...n\}}\right)
\]
证明

看起来组合意义很强...

这一步好像是理解Matrix Tree本质/性质/拓展性 的关键一步，可惜我看不懂....

---

回到正题= =

我们把\(B\)的第一列剔除，显然\(R=B'^TB'\) ，套公式有
\[
|R|=\sum_{|S|=n-1,S\subseteq\{1\dots m\}}\det\left(B'^T_{\{1...n-1\},S}\right)\det\left(B'_{S,\{1...n-1\}}\right)
\]
激动人心的时刻到了，根据矩阵转置的性质可以发现
\[
|R|=\sum_{|S|=n-1,S\subseteq\{1\dots m\}}\det\left(B'_{S,\{1...n-1\}}\right)^2
\]
好诱人的组合意义啊。不过我们做一点准备工作，搞个记号\(N=\{1...n-1\}\)。

• \(\det(B'_{S,N})^2 \in \{0,1\}\)

  可以发现的是，根据\(B'^T_{S,N}B'_{N,S}=R\)，当且仅当选出的边不连通时，可以知道\(\det (B'^T_{S,N})=\det(B'_{N,S})=0\)。

  现在要证明选出的边联通时，\(||B'_{N,S}||=1\)。此时由于\(|S|=n-1\)那么一定是一颗树。

  口胡警告

  观察\(B'_{N,S}\)这个矩阵的形式，应该是由初等基本变换变换出来的，然后我们又有\(B'^T_{S,N}B'_{N,S}=R,||R||=1\)，基本初等变换得到的矩阵相乘仍然可以看做基本初等变换，由于基本初等变化不会影响行列式的值，就有那么\(||B'_{N,S}||=1\) 。

现在回过头来考虑CB公式的算法，它相当于在\(O({m\choose n-1})\)时间内枚举每一个边集，然后判断是否联通，若联通就\(+1\)的贡献。显然最终累和的值就是生成树的个数。

也就是说|R|就等于这个图的生成树个数。

R是一个行列式，算行列式自然有好算的办法

啦啦啦终于证完了

下面的推广可能完全是假的。

推广

根据行列式的\(O(n!)\)的式子，可以知道\(|R|\)的值是关于\(|R_{ij}|\)的基本初等函数(加减乘除)。根据上面的推导，我们发现\(|R|\)是一堆\(1,-1\)的乘积的和。上面的推导中，不存在除法，虽然存在乘法但是是简单的取相反数运算。(注意，有平方运算!)我们如果将邻接矩阵的01换成边的边权\(w\)，那么\(|R|\)就等于所有生成树的边权积(注意，边权\(\in R^+\))的和。

因为行列式本质上是只是一个多元函数\(F(\{\})=\sum \prod (-1)^{?}...\)，我们甚至令w=一个生成函数甚至边权!!1...(毒瘤警告)

实际上我们计的数是，在\(m\)个三元组\((i,j,w)\)中选择\(n-1\)个出来，并且保证\((i,j)\)构成一棵树。我们求的是所有满足树条件的每棵树的\(\prod w\) 的和。

口胡警告

更抽象地讲，任何和域\(<R,+,\times>\)有着相同的代数结构的域\(<C,\and,*>\)都满足这个定理，可以得到\(|R|=\and *w\)。

注意到不论我们带什么进去都是好实现的，因为求行列式有\(O(n^3)\)的算法，而且...

这就触及到我的知识盲区了，理性证明等我大学看能不能学会，但是现在可以拍脑袋地讲，假如你有可以对应到加(减)乘(除)的运算法则的元素，那么你带进去没错。这是很对的。

所以:

• 假如让边权\(w\)等于这条边重边数量(度数也要相应更新)，那么\(|R|\)就等于考虑重边生成树个数。
• 有向图的生成树的话，\(D\)就要钦定是入/出度矩阵，\(A\)就要钦定是\(A_{i,j/j,i}=cnt[e<i,j>]\)，得到的\(|R_{ii}|\)是以\(i\)为根的内向树/外向树个数。正确性如果通过上面的证明理解的话貌似是完全错误的，因为就拉普拉斯矩阵的第一个性质就不满足...可能有别的构造出的组合意义?

至此，熟练背诵的Matrix Tree定理就出来了....