AcWing 243. 一个简单的整数问题2 | 树状数组

传送门

题目描述

给定一个长度为N的数列A，以及M条指令，每条指令可能是以下两种之一：

1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。

2、“Q l r”，表示询问 数列中第 l~r 个数的和。

对于每个询问，输出一个整数表示答案。

输入格式

第一行两个整数N,M。

第二行N个整数A[i]。

接下来M行表示M条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

1≤N,M≤1051≤N,M≤105,
|d|≤10000|d|≤10000,
|A[i]|≤1000000000|A[i]|≤1000000000

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

输出样例：

4
55
9
15

题解：我们知道树状数组的基本用途是维护序列的前缀和以及单点更新。我们可以用b数组维护a数组的单点更新改变的值，a[i]加上b数组的前缀和就能得到a[i]更新后的值。那我们怎么算更新后的区间和呢？我们求数组a的前缀和a[1~x]相当于求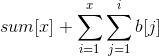，他可以写成：

　　

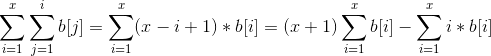
那么我们可以再用一个c数组来维护i*b[i]的前缀和。问题就变成了求(sum[r]+(r+1)*query(b,r)-query(c,r))-(sum[l-1]+l*query(b,l-1)-query(c1,l-1))

代码：

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned ll
using namespace std;
const int N = 1e5 + ;
const double eps = 1e-;
ll a[N],c[][N],sum[N];
int lowbit(int x) {return x&(-x);}
void add(int k,int x,int y) {
    while(x<N) {
        c[k][x]+=y;
        x += lowbit(x);
    }
}
ll query(int k,int x){
    ll ans = ;
    while(x) {
        ans += c[k][x];
        x -= lowbit(x);
    }
    return ans;
}
int main() {
    int n,m,l,r,x;
    char s[];
    scanf("%d%d",&n,&m);
    for (int i = ; i <= n; i++) {
        scanf("%lld",&a[i]);
        sum[i] = sum[i-] + a[i];
    }
    while(m--) {
        scanf("%s",s);
        if (s[] == 'Q') {
            scanf("%d%d",&l,&r);
            ll ans = sum[r]+(r+)*query(,r)-query(,r);
            ans -= sum[l-]+l*query(,l-)-query(,l-);
            printf("%lld\n",ans);
        }else if (s[] == 'C') {
            scanf("%d%d%d",&l,&r,&x);
            add(,l,x);
            add(,r+,-x);
            add(,l,l*x);
            add(,r+,-(r+)*x);
        }
    }
    return ;
}