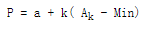opencv —— normalize 矩阵归一化
归一化:就是将数据通过某种算法,限制需要的一定范围内。
归一化的目的:简而言之,是使得没有可比性的数据变得具有可比性,同时又保持相比较的两个数据之间的相对关系,如大小关系;或是为了作图,原来很难在一张图上作出来,归一化后就可以很方便的给出图上的相对位置等。
矩阵归一化:normalize 函数
void normalize(InputArry src,InputOutputArray dst,double alpha = 1,double beta = 0,int norm_type = NORM_L2,int dtype = -1,InputArray mark = noArry())
- src,输入图像,Mat 类对象即可。
- dst,函数调用后的结果存在这里,和原图像具有一样的尺寸和类型。
- alpha,①值归一化,表示所乘系数;②范围归一化,表示范围界限,一般当作下界。
- beta,仅范围归一化用到,表示范围另一界限。
- norm_type,归一化选择的数学公式。
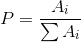
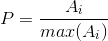

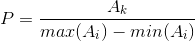
- dtype,为负时,输出图像深度等于输入图像,否则深度为 dtype 类型。一般选择默认值。
- mark,掩码。若有感兴趣区域,则只对该区域进行操作。
值归一化:所有 NORM_XXX 公式均可使用
alpha != 0,beta = 0,根据数学公式计算出来的所有值均 * alpha。
示例:alpha = 45



范围归一化:必须且仅可以使用 NORM_MINMAX 公式
alpha !=0,beta != 0,假设 alpha < beta,即归一化范围 [alpha,beta],简记为 [a,b]。
- 首先找到样本数据的最小值 Min 及最大值 Max
- 计算系数为:k =(b - a) / (Max - Min)
- 得到归一化到 [a,b] 区间的数据:
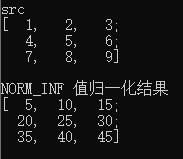
示例:alpha = 10,beta = 45

(呀呀,网上好多相关文章,但看完还是迷糊,现在终于明白了,(●'◡'●) 开心!)
opencv —— normalize 矩阵归一化的更多相关文章
- OpenCV在矩阵上的卷积
转载请注明出处!!!http://blog.csdn.net/zhonghuan1992 OpenCV在矩阵上的卷积 在openCV官网上说是戴面具,事实上就是又一次计算一下矩阵中的每个value,那 ...
- OpenCV利用矩阵实现图像旋转
利用OpenCV的矩阵操作实现图像的逆时针旋转90度操作 代码 Mat src = imread("C:\\Users\\fenggl\\Desktop\\测试.jpg",MREA ...
- OpenCV之图像归一化(normalize)
什么图像归一化 通俗地讲就是将矩阵的值通过某种方式变到某一个区间内 图像归一化的作用 目前能理解的就是归一化到某个区间便于处理,希望高人可以指点 opencv文档中的介绍 C++: void norm ...
- Opencv normalize
#include <iostream>#include <opencv2/opencv.hpp> using namespace std;using namespace cv; ...
- OpenCV的矩阵合并方法
有的时候我们需要将几个矩阵按行或者按列进行合并成一个大矩阵,这在Matlab里面非常的简单,但在OpenCV里面并没有这样的方法,现在我在OpenCV的源码里面发现合并矩阵的方法,分享给大家. A = ...
- OpenCV 对矩阵进行掩码操作
Mask operations on matrices https://docs.opencv.org/master/d7/d37/tutorial_mat_mask_operations.html ...
- 图像处理之 opencv 学习---矩阵的操作
OpenCV的一些操作,如生成随机矩阵,高斯矩阵,矩阵相乘之类的 /*功能:说明矩阵的一些操作方法*/#include "cv.h"//该头文件包含了#include " ...
- Opencv Mat矩阵中data、size、depth、elemSize、step等属性的理解
data: uchar类型的指针,指向Mat数据矩阵的首地址.可以理解为标示一个房屋的门牌号: dims: Mat矩阵的维度,若Mat是一个二维矩阵,则dims=2,三维则dims=3,大多数情况下处 ...
- matlab 工具函数 —— normalize(归一化数据)
function x = normalize(x, mu, sigma) x = bsxfun(@minus, x, mu); x = bsxfun(@rdivide, x, sigma); end ...
随机推荐
- python学习Day02
[主要内容] 1. 循环. while循环 while 条件: 代码块(循环体) 执行流程: 1. 判断条件是否为真. 如果真. 执行代码块 2. 再次判断条件是否为真...... 3. 当条件为假. ...
- 如何在OpenStack中对云主机类型进行重新配置
目标:很多用户在OpenStack启动一个虚拟机,选择了一个云主机配置类型,例如2CPU 4GB内存,使用了一段时间,感觉这个配置并不能满足需求,所以希望能够提高配置,那么OpeNStack的管理界面 ...
- 8、OSPF
OSPF ---最短路径优先 用于在单一自治系统(Autonomous System-AS)内决策路由 自制系统(AS)AS: 执行统一路由策略的一组网络设备的组合可适应大规模的网络: · 路由 ...
- CentOS 使用yum安装 pip
pip这个功能很不错,可以用来下载很多东西. 笔者使用的是CentOS Linux release 7.2.1511 (Core)这个版本. 查询版本的语句: cat /etc/redhat-rele ...
- 闲谈一下,ES3、ES4、ES5、ES6 分别是什么
上图按照时间顺序说明了JavaScript.JScript和ECMAScript的发展. 显示在网景工作的Brendan Eich临危受命,用十天时间设计出LiveScript的第一个版本.临时发布前 ...
- 01背包与完全背包(dp复习)
01背包和完全背包都是dp入门的经典,我的dp学的十分的水,借此更新博客的机会回顾一下 01背包:给定总容量为maxv的背包,有n件物品,第i件物品的的体积为w[i],价值为v[i],问如何选取才能是 ...
- Codeforces 961C Chessboard(将碎了的、染色乱了的棋盘碎片拼一起)
题目链接:点击打开链接 Magnus decided to play a classic chess game. Though what he saw in his locker shocked hi ...
- 《Python学习手册 第五版》 -第2章 Python如何运行程序
第二章主要讲解了Python的运行机制, 在开始之前,需要明确以下几点 因为<Python学习手册>这本书是面向市场很多人的,既然有很多人,就有很多不一样的需求和使用情况,这本书涵盖Pyt ...
- 转AngularJS路由插件
AngularJS学习笔记--002--Angular JS路由插件ui.router源码解析 标签: angular源码angularjs 2016-05-04 13:14 916人阅读 评论(0) ...
- oracle安装异常汇总
. 运行 ./runInstaller 安装界面出现乱码问题 解决方案: export NLS_LANG=AMERICAN_AMERICA.UTF8 export LC_ALL=C .运行 ./run ...