SpingMVC使用小结
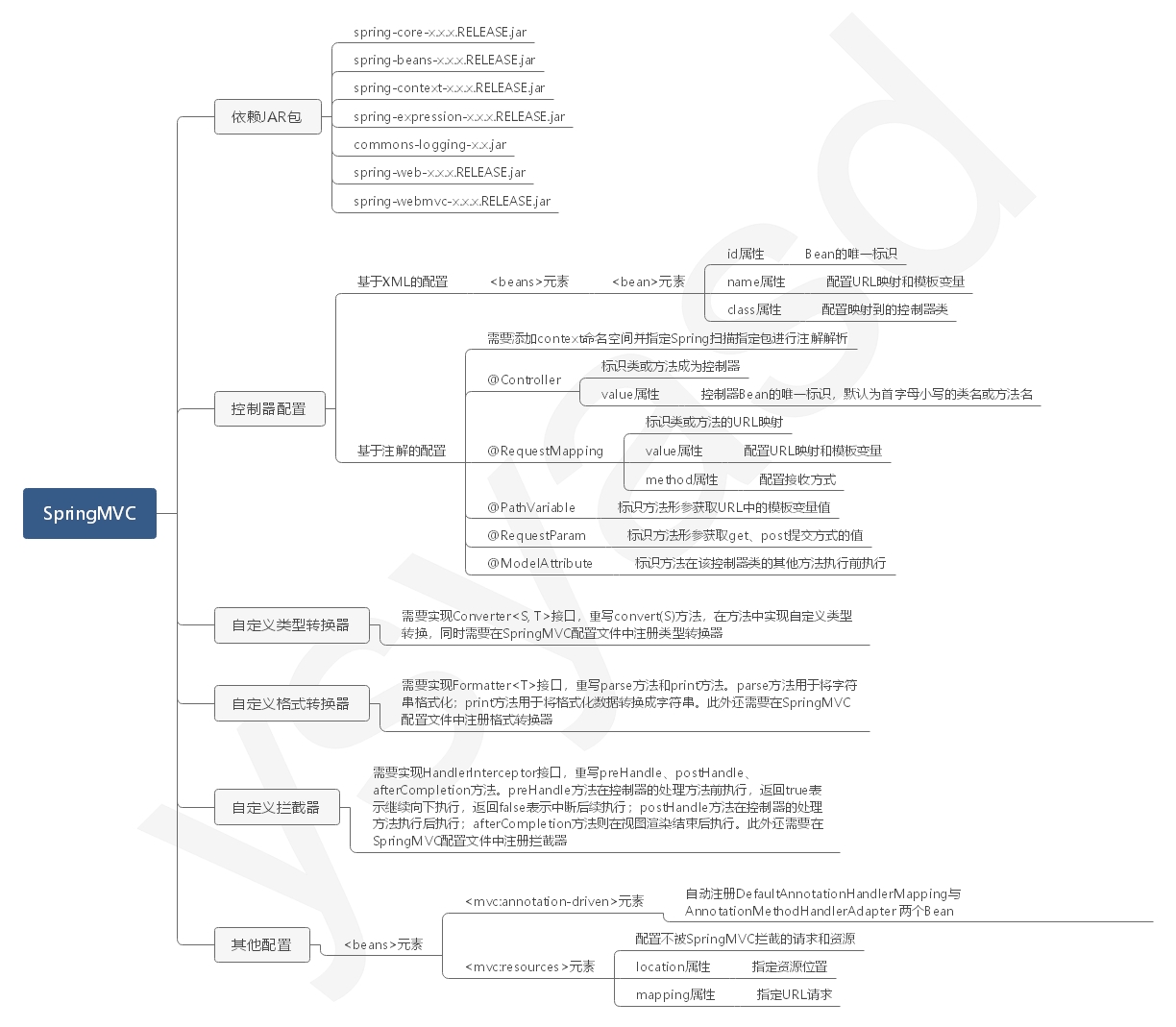
SpingMVC使用小结的更多相关文章
- 从零开始编写自己的C#框架(26)——小结
一直想写个总结,不过实在太忙了,所以一直拖啊拖啊,拖到现在,不过也好,有了这段时间的沉淀,发现自己又有了小小的进步.哈哈...... 原想框架开发的相关开发步骤.文档.代码.功能.部署等都简单的讲过了 ...
- Python自然语言处理工具小结
Python自然语言处理工具小结 作者:白宁超 2016年11月21日21:45:26 目录 [Python NLP]干货!详述Python NLTK下如何使用stanford NLP工具包(1) [ ...
- java单向加密算法小结(2)--MD5哈希算法
上一篇文章整理了Base64算法的相关知识,严格来说,Base64只能算是一种编码方式而非加密算法,这一篇要说的MD5,其实也不算是加密算法,而是一种哈希算法,即将目标文本转化为固定长度,不可逆的字符 ...
- iOS--->微信支付小结
iOS--->微信支付小结 说起支付,除了支付宝支付之外,微信支付也是我们三方支付中最重要的方式之一,承接上面总结的支付宝,接下来把微信支付也总结了一下 ***那么首先还是由公司去创建并申请使用 ...
- iOS 之UITextFiled/UITextView小结
一:编辑被键盘遮挡的问题 参考自:http://blog.csdn.net/windkisshao/article/details/21398521 1.自定方法 ,用于移动视图 -(void)mov ...
- K近邻法(KNN)原理小结
K近邻法(k-nearst neighbors,KNN)是一种很基本的机器学习方法了,在我们平常的生活中也会不自主的应用.比如,我们判断一个人的人品,只需要观察他来往最密切的几个人的人品好坏就可以得出 ...
- scikit-learn随机森林调参小结
在Bagging与随机森林算法原理小结中,我们对随机森林(Random Forest, 以下简称RF)的原理做了总结.本文就从实践的角度对RF做一个总结.重点讲述scikit-learn中RF的调参注 ...
- Bagging与随机森林算法原理小结
在集成学习原理小结中,我们讲到了集成学习有两个流派,一个是boosting派系,它的特点是各个弱学习器之间有依赖关系.另一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合. ...
- scikit-learn 梯度提升树(GBDT)调参小结
在梯度提升树(GBDT)原理小结中,我们对GBDT的原理做了总结,本文我们就从scikit-learn里GBDT的类库使用方法作一个总结,主要会关注调参中的一些要点. 1. scikit-learn ...
随机推荐
- Windows Storport Miniport 驱动开发 葵花宝典 - 翻译
Roadmap for Developing Storport Miniport Drivers Last Updated: 4/20/2017 To create a storport mini ...
- 绕过本机DNS缓存
--转载注明来源 http://www.cnblogs.com/sysnap/ 0x1 背景 往HOST文件添加127.0.0.1 www.baidu.com, 可以劫持百度的域名.病毒经常篡改HO ...
- adb的一些命令
adb pull <手机路径> <本机路径> 从手机中拉取信息到本地电脑上 adb push <本机路径> <手机路径> 从本地电脑推送信息到手机上
- Python 基础学习的几个小例子
最近在研究动态脚本语言 Python , 出于对其语言精简度的喜欢及大学时期对 matlab 这样的数学领域语言的怀念, 再加上笔者是C++起家,Python中所涉及的del机制与特殊方法重载(类比于 ...
- 在HTML中直接使用onclick很不专业
原因 1.onclick添加的事件处理函数是在全局环境下执行的,这污染了全局环境,很容易产生意料不到的后果: 2.给很多DOM元素添加onclick事件,可能会影响网页的性能,毕竟网页需要的事件处理函 ...
- go一个简单的爬虫(豆瓣)
最近在学习go语言爬虫,写了个小demo package main import ( "fmt" "io/ioutil" "net/http" ...
- Linux-文件系统的简单操作
文件系统的简单操作 磁盘与目录的容量:df.du df [option] [目录或文件名] 参数: -a:列出所有的文件系统,包括系统特有的/proc等系统 -k:以KB的容量显示各文件系统 -m:以 ...
- setInterval、clearInterval的回调函数,实现函数间调用的先后顺序
定义: var waitUnitil=function (untillCallBack, nextStepCallBack, count) { if (count == null) { count = ...
- 容器时代的持续交付工具---Drone:Drone使用
上一篇文章里已经介绍了如何安装Drone,下面我们来看下如何使用.还是基于gogs作为git仓储. 首先打开server对应的地址,进入登录页面,输入在启动server时配置的管理员账号(对应的就是g ...
- vscode使用Chrome浏览器调试不好用,解决方法!!
1.如果你是刚下载vscode,那么你需要下载两个插件. 1. open in browser(在浏览器中查看,支持五大主流浏览器),下载并启用. 2. view-in-browser (在浏览器中查 ...
