leetcode题目142.环形链表Ⅱ(中等)

题目描述：

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

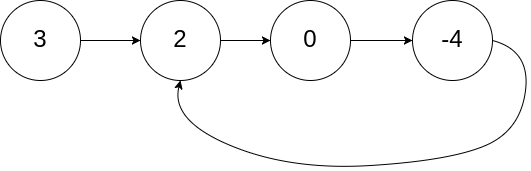
示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

进阶：
你是否可以不用额外空间解决此题？

思路分析：

思路一: 哈希, 空间复杂度O(n)O(n)

这个很好考虑, 把遍历过的节点记录,当发现遍历的节点下一个节点遍历过, 返回它

public class Solution {
    public ListNode detectCycle(ListNode head) {
        Set<ListNode> lookup = new HashSet<>();
        ListNode p = head;
        while (p != null) {
            lookup.add(p);
            if (lookup.contains(p.next)) return p.next;
            p = p.next;
        }
        return null;
    }
}

思路二 : 快慢指针(题解来自@paocai大神：https://leetcode-cn.com/u/powcai/)

说一下算法思路:

先用快慢指针, 找到他们相遇点(如果存在环)
再重新从链表头开始, 以及步骤1的相遇点, 两个位置一起走, 再次相遇就是环的入口

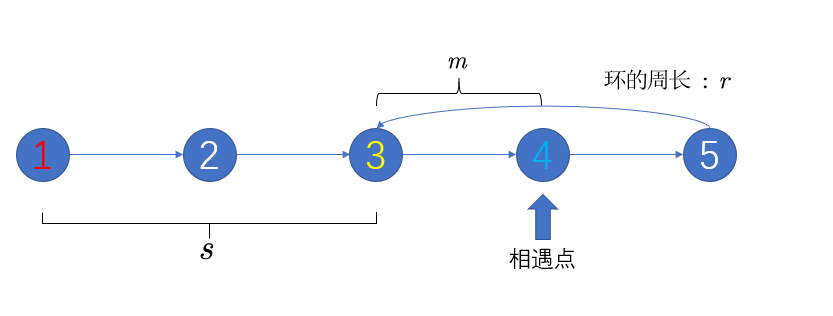
有三个节点需要注意: 起始节点(head), 环的入口节点(输出结果), 相遇的节点(快慢指针求的)

我们要证明 : 初始点到环的入口的步数 等于 相遇点到环入口的步数

我们令, 初始点到入口为 s, 入口到相遇点 m, 环的周长为 r

我们只需证明: s == r - m

首先我们假设,慢指针走了 k 步到相遇点, 那么快指针就是 2k 步,所以我们有 2k - k = nr 即 k = nr(慢指针还没到环,快指针已经转了好几圈)

还有, s = k - m

得 : s = nr - m ==> s == (n - 1) r + (r - m)

得证!

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) return null;
        ListNode slow = head;
        ListNode fast = head;
        ListNode start = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                while (start != slow) {
                    slow = slow.next;
                    start = start.next;
                }
                return slow;
            }
        }
        return null;
    }
}