Reservoir Sampling 蓄水池采样算法

https://blog.csdn.net/huagong_adu/article/details/7619665

https://www.jianshu.com/p/63f6cf19923d

https://www.cnblogs.com/snowInPluto/p/5996269.html

https://www.cnblogs.com/xudong-bupt/p/4053652.html

https://www.jianshu.com/p/51f7089c082b

概念：

在一个给定长度的数组中随机等概率抽取一个数据很容易，但如果面对的是长度未知的海量数据流呢？蓄水池采样(Reservoir Sampling)算法就是来解决这个问题的, 它在分析一些大数据集的时候非常有用。

场景说明：

1. 从一个字符流中进行采样，最后保留 10 个字符，而并不知道这个流什么时候结束，且须保证每个字符被采样到的几率相同。
2. 应用场景场景说明：在一个海量广告数据中抽样100个query，其中特征包含pv（query的搜索次数）、adpv（出广告的搜索次数）、adshow（出广告之后的总共ad展示量）、click（点击数量）

蓄水池抽样：每次随机生成一个数(0,1)值u，令a = u^(1/pv)，循环n次，直到结束取前100个大的a值。

算法过程

1. 假设原始数据规模为n，需要采样的数量为k
2. 先选取数据流中的前k个元素，保存在集合A中；
3. 从第j（k + 1 <= j <= n）个元素开始，每次先以概率p = k/j选择是否让第j个元素留下。若j被选中，则从A中随机选择一个元素并用该元素j替换它；否则直接淘汰该元素；
4. 重复步骤3直到结束，最后集合A中剩下的就是保证随机抽取的k个元素。

数学归纳法证明：

• 　　　当n=k是，显然“蓄水池”中任何一个数都满足，保留这个数的概率为k/k。
• 假设当n=m(m>k)时，“蓄水池”中任何一个数都满足，保留这个数的概率为k/m。
• 当n=m+1时，以k/(m+1)的概率取A_n，并以1/k的概率，随机替换“蓄水池”中的某个元素，否则“蓄水池”数组不变。则数组中保留下来的数的概率为：

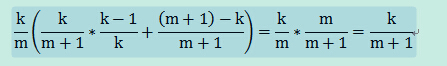
所以，对于第n个数A_n，以k/n的概率取A_n并以1/k的概率随机替换“蓄水池”中的某个元素；否则“蓄水池”数组不变。依次类推，可以保证取到数据的随机性。

Java实现的代码：

public class ReservoirSamplingTest {

    private int[] pool; // 所有数据
    private final int N = 100000; // 数据规模
    private Random random = new Random();

    @Before
    public void setUp() throws Exception {
        // 初始化
        pool = new int[N];
        for (int i = 0; i < N; i++) {
            pool[i] = i;
        }
    }

    private int[] sampling(int K) {
        int[] result = new int[K];
        for (int i = 0; i < K; i++) { // 前 K 个元素直接放入数组中
            result[i] = pool[i];
        }

        for (int i = K; i < N; i++) { // K + 1 个元素开始进行概率采样
            int r = random.nextInt(i + 1);
            if (r < K) {
                result[r] = pool[i];
            }
        }

        return result;
    }

    @Test
    public void test() throws Exception {
        for (int i : sampling(100)) {
            System.out.println(i);
        }
    }
}

C++实现的代码：

int num = rand() % n +a;  //其中的a是起始值，n-1+a是终止值，n是整数的范围。

  //在序列流中取n个数，保证均匀，即取出数据的概率为:n/(已读取数据个数)
  void RandKNum(int n){
      int *myarray=new int[n];
      for(int i=;i<n;i++)
          cin>>myarray[i];

      int tmp=;
      int num=n;
      while(cin>>tmp){
         if(rand()%(num+)+<n)
             myarray[rand()%n]=tmp;
     }

     for(int i=;i<n;i++)
         cout<<myarray[i]<<endl;
 }