2019.7.9 校内测试 T1挖地雷

这一次是交流测试？边交流边测试（滑稽

挖地雷

这个题是一个递推问题。

首先我们看第一个格子，因为它只影响了它的上面和右上面这两个地方是否有雷。

我们可以分3种情况讨论：

1. 第一个格子的数字是2；

2. 第一个格子的数字是1；

3. 第一个格子的数字是0；

显然对于第1种情况和第3种情况，我们可以确定前两个空的埋雷情况：

第1种情况就是前两个空都埋雷了，第3种情况就是钱两个空都没有埋雷；

第二种情况我们需要再往下细分：第一个空埋雷，第二个空不埋雷；第一个空不埋雷，第二个空埋雷；

我们根据样例来分析递推情况：

首先根据第一个格子的数字是2，我们可以推断出前两个空肯定是有雷的：

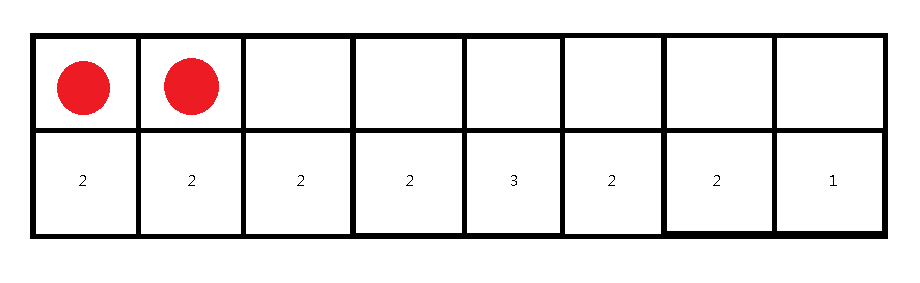
接下来我们考虑第二个格子上的数字对埋雷情况造成的影响，考虑到我们在考虑第 i 个格子上的数字时，第 1~i 个空已经确定下来了（是否埋雷），所以对于第2个格子及以后，它真正能确定的空也就是第 i + 1 个，根据样例可知，第三个空是不埋雷的：

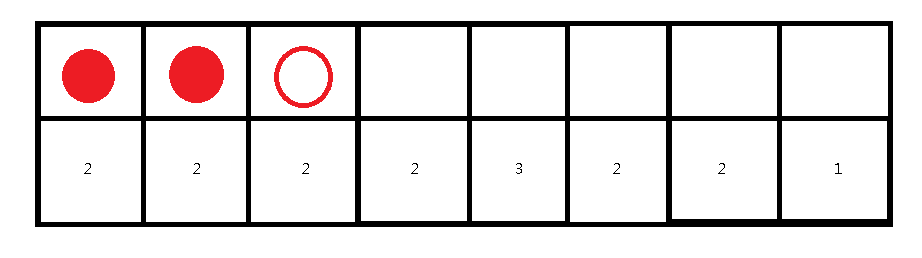
接下来考虑第三个格子上的数字对埋雷情况造成的影响，前三个空已经确定了，所以只能确定第四个空的情况，根据样例可知，第四个空是埋雷的：

以此类推，当我们考虑第 i 个格子上的数字对答案造成的影响的时候，实际上只能确定第 i + 1 个空的情况，对于具体的是否埋雷，我们还要看第 i - 1 ，i 个空的埋雷情况与第 i 个格子的数字的关系，轻松得到如下关系：

我们设 tot 是第 i - 1 ~ i 个空埋了多少个雷，vis [ i ] 表示第 i 个空是否埋雷，a [ i ] 表示第 i 个格子的数字是多少，则 tot 可以用下面一段代码求出：

    for(int i=k-;i<=k;i++)      //当前考虑第k个格子上的数字对答案的影响
        if(vis[i]) tot++;

有了这个 tot 有什么用呢？它决定着第 i + 1 个空是否埋雷，特别的，还能判断是否有解！

若 a [ k ] - tot = 1，说明第 i + 1个空需要埋雷；

若 a [ k ] - tot = 0，说明第 i + 1个空不需要埋雷；

若 a [ k ] - tot >=2，说明无解；                               //一个格子最多放一个雷，你却还有两个以上的雷需要放，肯定无解

若 a [ k ] - tot < 0；说明无解；                                //明明只需要放 a [ k ] 个，你光前两个空放的都比 a [ k ] 多了，肯定无解

说句题外话，第四个关系式我当时没想到，然后就 65 了QwQ~

代码也很好写，就是这样的（其实就是套上去的）：

    if(a[k]-tot==) vis[k+]=;
    if(a[k]-tot==) vis[k+]=;
    if(a[k]-tot>=) return ;   //一个格子最多放一个雷,你却还有两个以上的雷需要放,肯定无解
    if(a[k]-tot<) return ;    //明明只需要放a[k]个,你光前两个空放的都比a[k]多了,肯定无解
    search(k+);               //找下一个格子

还有一个小细节需要考虑到：

我们前面已经说了第 i 个格子的数字的实际影响是第 i + 1个空，所以说我们遍历第 n - 1个格子的时候不就把雷给埋完了？那第 n 个格子有啥子用？

这里我就用第 n 个格子的数字再来判断一下我们的埋雷情况是否合法，当我们遍历到第 n 个格子时，我们需要看一下 vis [ n - 1 ] + vis [ n ] 是否等于 a [ n ] 即可。

So ，我们就可以上完整代码啦：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,bj,tot;
int a[],vis[];
void search(int k)
{
    tot=;                     //在k对应的三个格子中,已经埋了多少雷
    for(int i=k-;i<=k;i++)
    if(vis[i]) tot++;          //求tot
    if(k==n)                   //当我们遍历第n个格子,进一步判断是否合法
    {
        if(a[n]==tot) bj=;    //如果等于,说明合法
        return ;
    }
    if(a[k]-tot==) vis[k+]=;
    if(a[k]-tot==) vis[k+]=;
    if(a[k]-tot>=) return ;   //一个格子最多放一个雷,你却还有两个以上的雷需要放,肯定无解
    if(a[k]-tot<) return ;    //明明只需要放a[k]个,你光前两个空放的都比a[k]多了,肯定无解
    search(k+);               //找下一个格子
}
int main()
{
    //freopen("bomp.in","r",stdin);
    //freopen("bomp.out","w",stdout);
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
        if(a[i]<||a[i]>)     //这里好坑的,一定要特判一下
        {
            cout<<"No answer"<<endl;
            return ;
        }
    }
    if(a[]==)                //分情况讨论
    {
        vis[]=;
        vis[]=;
        search();
    }
    if(a[]==) search();
    if(a[]==)                //细分埋一个雷的情况
    {
        vis[]=;              //先使第一个空埋雷
        search();
        if(!bj)                //没找到解再让第二个空埋雷
        {
            memset(vis,,sizeof(vis));
            vis[]=;
            search();
        }
    }
    if(bj)
    {
        for(int i=;i<=n;i++)
        cout<<vis[i]<<" ";
    }
    else cout<<"No answer"<<endl;
    return ;
}