POJ 1984 Navigation Nightmare

并查集，给n个点和m条边，每条边有方向和长度，再给q个询问，第i个询问查询两个点之间在Ti时刻时的曼哈顿距离（能连通则输出曼哈顿距离，否则输出-1）

这题跟Corporative Network 有点像，只不过那题是维护到根节点的距离，这题还要顺便维护与根节点的x,y方向的偏移量。findset时，每次找完father就要加上father的x、y坐标偏移量，这样findset完以后就得到了与根的偏移量。然后合并时, （注意，这里是 fa[x] = y）

dr[x].x = r.x - dr[r.u].x + dr[r.v].x;

dr[x].y = r.y - dr[r.u].y + dr[r.v].y;      即 x->y <==> u->v - u->x + v->y 如下图：

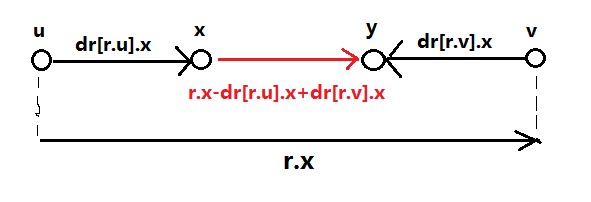
这题还要注意数据可能不是按照时间顺序输入的，要做一个排序，然后再按原来的顺序输出。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 40100

int fa[N],q;

struct DR
{
    int x,y;
}dr[N],to[];

struct ROAD
{
    int u,v;
    int x,y;
}road[N];

struct QUERY
{
    int a,b,time;
    int id,res;
}query[N];

void makeset(int n)
{
    for(int i=;i<=n;i++)
    {
        fa[i] = i;
        dr[i].x = dr[i].y = ;
    }
}

int findset(int x)
{
    if(x != fa[x])
    {
        int tmp = fa[x];
        fa[x] = findset(fa[x]);
        dr[x].x += dr[tmp].x;
        dr[x].y += dr[tmp].y;
    }
    return fa[x];
}

void unionset(int index)  //合并第index条边
{
    ROAD r = road[index];
    int x = findset(r.u);
    int y = findset(r.v);
    if(x == y)
        return;
    fa[x] = y;
    dr[x].x = r.x - dr[r.u].x + dr[r.v].x;   // x->y <==> u->v - u->x + v->y
    dr[x].y = r.y - dr[r.u].y + dr[r.v].y;
}

int cmp1(QUERY ka,QUERY kb)
{
    return ka.time<kb.time;
}

int cmp2(QUERY ka,QUERY kb)
{
    return ka.id<kb.id;
}

void InitDirection()
{
    to['E'-'A'].x = ;
    to['E'-'A'].y = ;
    to['W'-'A'].x = -;
    to['W'-'A'].y = ;
    to['N'-'A'].x = ;
    to['N'-'A'].y = ;
    to['S'-'A'].x = ;
    to['S'-'A'].y = -;
}

void read()
{
    int n,m,i,dis;
    char ss[];
    InitDirection();
    scanf("%d%d",&n,&m);
    makeset(n);
    for(i=;i<=m;i++)
    {
        scanf("%d%d%d %s",&road[i].u,&road[i].v,&dis,ss);
        road[i].x = dis*(to[ss[]-'A'].x);
        road[i].y = dis*(to[ss[]-'A'].y);
    }
    scanf("%d",&q);
    for(i=;i<=q;i++)
    {
        scanf("%d%d%d",&query[i].a,&query[i].b,&query[i].time);
        query[i].id = i;
    }
    sort(query+,query+q+,cmp1);
}

void solve()
{
    int i,j;
    j=;
    for(i=;i<=q;i++)
    {
        for(;j<=query[i].time;j++)
        {
            unionset(j);
        }
        if(findset(query[i].a) != findset(query[i].b))
            query[i].res = -;
        else
            query[i].res = abs(dr[query[i].a].x-dr[query[i].b].x) + abs(dr[query[i].a].y-dr[query[i].b].y);
    }
    sort(query+,query+q+,cmp2);
    for(i=;i<=q;i++)
        cout<<query[i].res<<endl;
}

int main()
{
    read();
    solve();
    return ;
}