Shell排序（改良的插入排序）

Shell排序算法最初是由D.L Shell于1959年提出，假设要排序的元素有n个，则每个进行插入排序是并不是所偶的元素同时进行，而是去一段间隔。

Shell首先将间隔设定为n/2，然后跳跃的进行插入排序，再来将间隔设定为n/4，跳跃进行排序动作，再来设定时间间隔为n/8、n/16，知道间隔为1之后的最后一次排序终止，由于上一次的排序动作都会将固定间隔内的元素排序好，所以当间隔为1之后的最后一次排序终止，由于上一次的排序动作都会将固定间隔内的元素排序好，所以当间隔越来越小时，某些元素位于正确位置的几率越高，因此最后几次的排序动作将可以大幅减低。

举个例子来说，假如有一未排序的数字如右：89 12 65 97 61 81 27 2 61 98

数字的总数共有10个，所以第一次我们将间隔设定为10/2=5，此时我们对间隔为5的数字进行排序，如下所示：

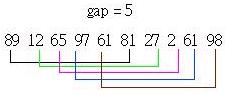
总结连线的部分表示要一起进行排序的部分，再来将间隔设定为5/2的商，也就是2，则第二次的插入排序对象如下所示：

再来间隔设定为2/2=1，此时就是单纯的插入排序了，由于大部分的元素都已大致排序过了，所以最后一次的插入排序机会没有什么排序动作了：

将间隔设定为n/2是D.L Shell最初所提出，在教科书中使用这个间隔比较好说明，然而Shell排序法的关键在于间隔的设定，例如Sedgewick证明选用以下的间隔可以加快Shell排序算法的速度：

其中4*(2j)2 + 3*(2j) + 1不可超过元素总数n值，使用上式找出j后代入4*(2j)2 + 3*(2j) + 1求得第一个间隔，然后将2j除以2代入求得第二个间隔，再来依次类推。

后来还有人证明有其它的间隔选定方法可以将Shell排序算法的速度再加快；另外Shell排序算法的概念也可以用来改良冒泡排序算法。

C#实例：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

private static void ShellSort() {     int[] num = new int[] { 70, 80, 31, 37, 10, 11, 48, 60, 33, 80 };     int length = num.Length;     int gap = length / 2;       WriteNumLine(num);       while (gap > 0)     {         for (int k = 0; k < gap; k++)         {             for (int i = k + gap; i < length; i += gap)             {                 for (int j = i - gap; j >= k; j -= gap)                 {                     if (num[j] > num[j + gap])                     {                         int temp = num[j + gap];                         num[j + gap] = num[j];                         num[j] = temp;                     }                     else                     {                         break;                     }                 }             }         }         gap = gap / 2;           WriteNumLine(num);     }       WriteNumLine(num); }   private static void WriteNumLine(int[] num) {     foreach (int i in num)     {         Console.Write(i + " ");     }     Console.WriteLine(); }