算法：Manacher,给定一个字符串str,返回str中最长回文子串的长度。

【题目】

给定一个字符串str,返回str中最长回文子串的长度

【举例】

str="123", 1

str=“abc1234321ab” 7

【暴力破解】

从左到右遍历字符串，遍历到每个字符的时候，以当前字符作为中心能够产生多大的回文字符串，

奇回文和偶 回文寻找方式不一样。

缺点：前面的寻找无法为后面的寻找提供任何帮助。没有记忆。加上记忆就好了。

【Manacher】

Manacher算法解决的问题是在线性时间内找到一个字符串的最长回文子串。

1. 奇回文和偶回味在判断是比较麻烦，首先对str进行处理。插入 特殊字符。
   
   123 -》 #1#2#3#

通过这种处理方式，偶回文也有了中心轴。 解决了奇偶的差异性。

特殊字符# 用于对应的是自己。所以对整个求解无影响。

其中用到 i & 1 判断当前索引是 奇数还是偶数。参考这个

https://segmentfault.com/q/1010000021162482/a-1020000021164176

public static char[] manacherString(String str) {
        char[] charArr = str.toCharArray();
        char[] res = new char[2 * charArr.length + 1];
        int index = 0;
        for (int i = 0; i < res.length; i++) {
            // i&1==0 表示 如果是 偶数
            res[i] = (i & 1) == 0 ? '#' : charArr[index++];
        }
        return res;
    }

1. 处理后的字符串记为charArr.
   
   需要三个辅助变量

• pArr: 长度与charArr长度一样。pArr[i]的含义是： 以 i 位置上的字符 charArr[i]作为 回文中心的情况下，扩出去得到的最大回文半径是多少。
• pR: 这个变量是 之前遍历的所有 字符的所有回文半径中。 最右即将到达的位置。
• index: 和pR联动。表示最右即将到达的位置 的回文中心位置。

3）从左到右依次算出数组pArr每个位置的值，最大的值 就是处理后的charArr中的最大回文半径。

中括号表示 index的回文左右边界。

小括号表示 i 和 i'的左右回文边界。

分俩大情况， 第二种情况再分为3小情况。

• 第一种情况
  
  

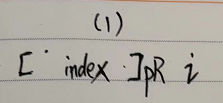
当前的i，在pR之后，就暴力扩就对了。前面的回文信息提供不了任何帮助。

• 第二种情况
  
  就是 i在pR之内。
  
  

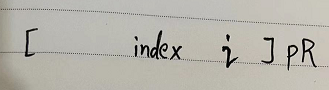
index肯定在 i之前。

因为 i在 某一个元素的回文半径中，所以一定有对称点i'

根据i'的回文半径所处位置划分为三类

1）i'的回文半径 在 index的回文半径内。



i的回文半径就是和i'一样，不可能再大了。

证明：

首先X != Y

Y和Z是 index的对称点。 Y == Z

X和H是 index的对称点。 X == H

所以 Z != H 。所以 i的回文半径长度就是pArr[i']

2) i'的回文半径 超出了index的回文半径



]' [' 代表 以 i' 和 i 为对称的 []的位置。

现在证明 i的 最大回文半径应该是多少呢.

首先 [' 到 ]的位置肯定是回文。只需要看Z和H是否相等。

证明：

X和Y是 以 i'的对称点 。 X == Y。

Y和Z是 以 index的对称点。 Y==Z。 那么 X == Z。

X和H肯定不相等。因为如果相等。那么 index的最大回文半径就不是[]。 X!=H

那么Z!=H

那么 i的回文半径长度 就是 [' 到 ]

3）i'的回文半径 正好 和index的左边界 重合。

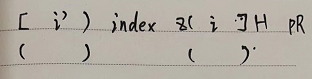
那么i最小的回文也是（到]。 因为Z和H是否相无法证明，需要比较了。

以上三种情况，扩出去的过程可以优化，但还是无法 避免扩出去的检查。

public static int maxLcpsLength(String str) {

        if (str == null || str.length() == 0) {
            return 0;
        }

        char[] charArr = manacherString(str);
        System.out.println(Arrays.toString(charArr));
        int[] pArr = new int[charArr.length];
        int index = -1;
        int pR = -1;
        int max = Integer.MIN_VALUE; // 保存最大值。

        for (int i = 0; i < charArr.length; i++) {

            if (pR > i) {
                // i 在 pR内，看哪部分不需要比较了。

                // i' 的 位置的 回文半径 大小
                int pi_ = pArr[2 * index - i];

                // 最远也只能扩到 pR . 最小 就是 看i'的回文半径 pi_

                int pR_pi_ = pR - i; // i 到 pR的距离长度大小。
                // 取最小值.三种情况都符合，也没有多余的浪费。
                // 第一种。pR-i 肯定 大于 pi_ 所以没问题
                // 第二种. pR-i 肯定 小于 pi_ 本来就是从pR开始扩，也没问题。
                // 第三种. pR-i == pi_ 。
                pArr[i] = Math.min(pi_, pR_pi_); // 当前 pArr[i] 的值得意思是 以 i为中心，这个半径之内的不需要验证了。后面的还需要比较一下。

            } else {
                // i 在 pR外。需要自己扩。
                pArr[i] = 1;
            }
            // 以上 整合成一行就是
            // pArr[i] = pR > i ? Math.min(pArr[2*index-1], pR-i):1;
            while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
                // 扩的停止条件就是 左右边界到了。
                if (charArr[i + pArr[i]] == charArr[i - pArr[i]]) {
                    pArr[i]++;// 左右相等。继续扩。
                } else {
                    // 无法继续扩了，退出。
                    break;
                }
                // 更新 pR 和 index ,如果当前 i位置的最右边界 和前面的一样，不更新。只有大于才更新。
                if (i + pArr[i] > pR) {
                    pR = i + pArr[i];
                    index = i;
                }
                // 更新max
                max = Math.max(max, pArr[i]);
            }
        }

        return max - 1; //

    }

max - 1 ，因为 加了辅助。需要减一。