文心一言 VS chatgpt （7）-- 算法导论2.3 3~4题

三、使用数学归纳法证明:当n刚好是2的幂时，以下递归式的解是 T(n)=nlgn。若n=2，T(n)=2；若n=2^k,k>1，T(n)=2T(n/2)+n。

文心一言：

chatgpt：

首先，当 n=2 时，T(n)=2log₂n=2，显然等式成立。

现假设对于所有的 k<m，递归式 T(n)=nlgn 成立，即当 n 刚好是 2 的幂时，T(n)=nlgn。

考虑当 n=2^m 时，如何证明 T(n)=nlgn。

根据递归式，有：

T(n) = 2T(n/2) + n

将 n=2^m 带入上式，可以得到：

T(2^m) = 2T(2^(m-1)) + 2^m

由于 2^(m-1) 是 2 的幂，根据归纳假设，可以得到：

T(2^(m-1)) = (2^(m-1)) * lg(2^(m-1)) = (m-1)2^(m-1)

带回原式，得：

T(2^m) = 2T(2^(m-1)) + 2^m
= 2((m-1)2^(m-1)) + 2^m
= m2^m

因此，当 n=2^m 时，T(n)=nlgn 成立。

综上所述，由数学归纳法可知：当 n 刚好是 2 的幂时，递归式 T(n)=nlgn 的解为 T(n)=nlgn。

四、我们可以把插人排序表示为如下的一个递归过程。为了排序 A[1…n]，我们递归地排序A[1…n-1]，然后把 A[n]插入已排序的数组 A[1…n-1]。为插人排序的这个递归版本的最坏情况运行时间写一个递归式。

文心一言：

为了排序 A[1…n]，我们递归地排序A[1…n-1]，然后把 A[n]插入已排序的数组 A[1…n-1]。为插人排序的这个递归版本的最坏情况运行时间写一个递归式。

最坏情况下，我们需要遍历整个数组，因此递归深度为 n。在每个递归步骤中，我们需要检查是否需要插入新元素，因此递归深度为 n-1。因此，插入排序的最坏情况运行时间为 O(n^2)。

chatgpt：

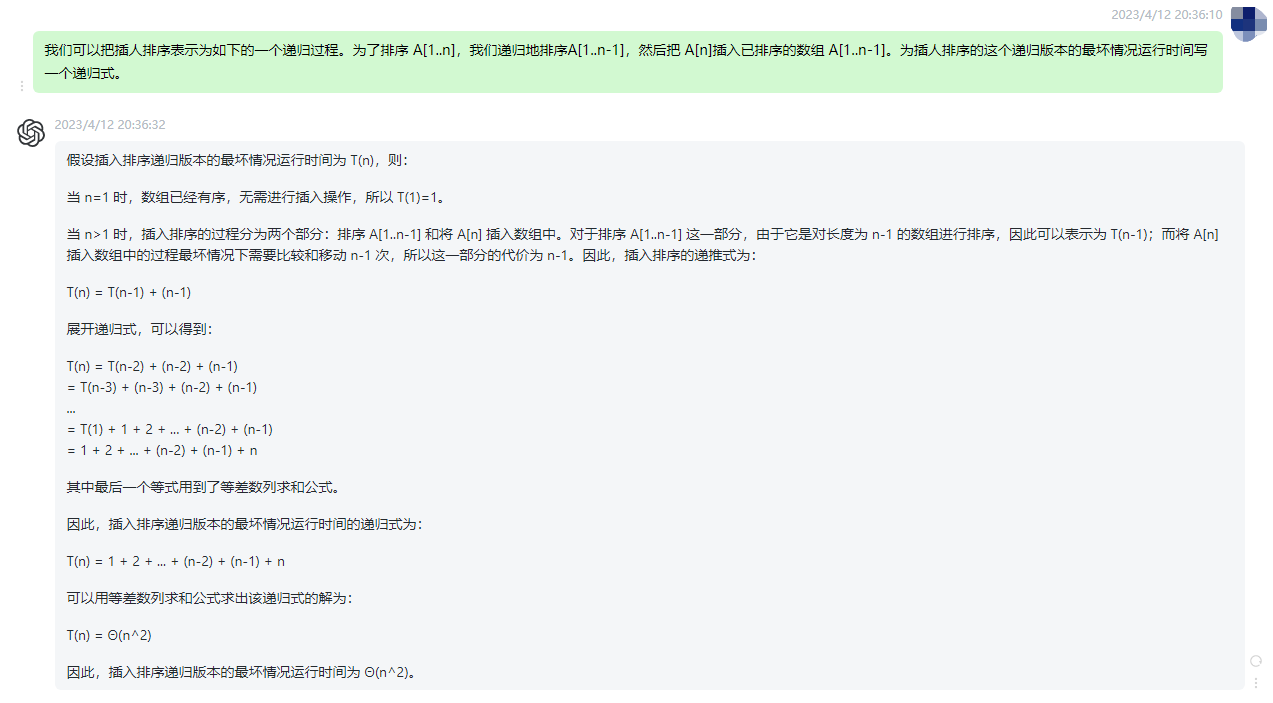
假设插入排序递归版本的最坏情况运行时间为 T(n)，则：

当 n=1 时，数组已经有序，无需进行插入操作，所以 T(1)=1。

当 n>1 时，插入排序的过程分为两个部分：排序 A[1…n-1] 和将 A[n] 插入数组中。对于排序 A[1…n-1] 这一部分，由于它是对长度为 n-1 的数组进行排序，因此可以表示为 T(n-1)；而将 A[n] 插入数组中的过程最坏情况下需要比较和移动 n-1 次，所以这一部分的代价为 n-1。因此，插入排序的递推式为：

T(n) = T(n-1) + (n-1)

展开递归式，可以得到：

T(n) = T(n-2) + (n-2) + (n-1)
= T(n-3) + (n-3) + (n-2) + (n-1)
…
= T(1) + 1 + 2 + … + (n-2) + (n-1)
= 1 + 2 + … + (n-2) + (n-1) + n

其中最后一个等式用到了等差数列求和公式。

因此，插入排序递归版本的最坏情况运行时间的递归式为：

T(n) = 1 + 2 + … + (n-2) + (n-1) + n

可以用等差数列求和公式求出该递归式的解为：

T(n) = Θ(n^2)

因此，插入排序递归版本的最坏情况运行时间为 Θ(n^2)。