Atcoder Regular Contest 093 C - Bichrome Spanning Tree

给定一张图，对图上边黑白染色，使得同时选择了两种颜色边的最小生成树边权和为X，求染色方案数。

先求出图的\(mst\)大小，然后分三类讨论：

1.\(X<mst\) 无解

2.\(X==mst\)

我们求出可以构成最小生成树的边集大小\(sumst\)。

可以发现，在这个边集里，只要不是所有边颜色相同，就一定能构造出有双色边的原图\(mst\)。边补集则可以任意染色 ;w;

方案数是\(2^{m-sumst}*(2^{sumst}-2)\)

3.\(X>mst\)

我们考虑在\(mst\)上强制加一条边对\(mst\)的贡献。

画个有点丑的树（）这是某个原图的一个\(mst\)。

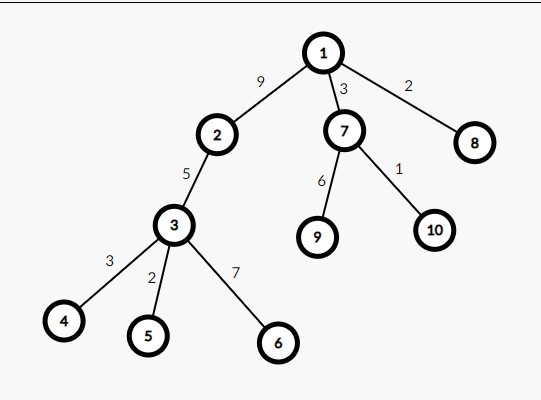
现在考虑强制连一条边\((3,9)\)，\(w=13\)

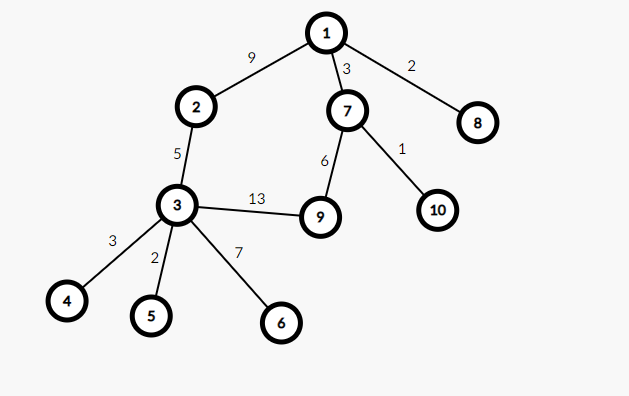
要让其重新变成一棵树，就要在\((3,9)\)这条链上删去一条边（）显然是应该删去最大的那条，即\((1,2)\)，\(w=9\)

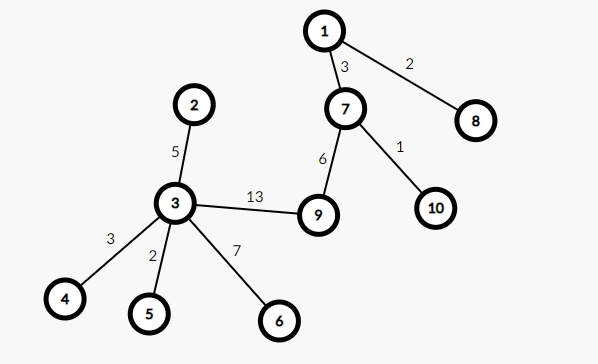
草，搞这么多不就一句话QAQ

一条边(u,v)的贡献就是\(v[i]=w[u,v]-maxw(u,v)\)

这样我们就可以用树剖+RMQ求得每条边对mst的贡献（）

这样我们可以统计出对mst的贡献\(v[i]=X-mst\)的边数\(sum1\)

这样我们要使得mst边集边全部同色，sum1边集至少有一边异色，剩余的边补集任意染色。实际操作的时候我通过判断w[i]-v[i]>X-mst统计了边补集的大小sum2

方案数为\(2^{sum2}*(2^{sum1}*2-2)\)

以及第二个分类中的sumst其实是=sum1+n-1的（很显然吧x）

因为ST表我不大会写，还是写了线段树来着（

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define MAXN (int)(1e3+7)
#define MAXM (int)(2e3+14)
#define mod (int)(1e9+7)
using namespace std;
int n,m;
long long X;
struct edge
{
	int x,y,z;
}a[MAXM];
struct qwq
{
	int nex,to,w;
}e[MAXN<<1];
int h[MAXN],tot=0;
inline void add(int u,int v,int w)
{
	e[++tot].to=v;
	e[tot].nex=h[u];
	e[tot].w=w;
	h[u]=tot;
}
inline long long power(long long a,long long b)
{
	long long answer=1,base=a;
	while (b)
	{
		if (b&1)
		{
			answer*=base;
			answer%=mod;
		}
		b>>=1;
		base*=base;
		base%=mod;
	}
	return answer;
}
inline bool cmp(edge aa,edge bb) { return aa.z<bb.z; }
int fa[MAXN];
long long mst=0;
int sum3=0;
inline void INIT1() { for (int i=1;i<=n;i++) fa[i]=i; }
inline void INIT2() { for (int i=1;i<=n;i++) fa[i]=0; }
int found(int x) { if (x==fa[x]) return x; return fa[x]=found(fa[x]); }
bool book[MAXM];
inline void MST()
{
	INIT1();
	sort(a+1,a+m+1,cmp);
	for (int i=1,fx,fy;i<=m;i++)
	{
		fx=found(a[i].x); fy=found(a[i].y);
		if (fx!=fy)
		{
			fa[fx]=fy;
			add(a[i].x,a[i].y,a[i].z);
			add(a[i].y,a[i].x,a[i].z);
			mst+=a[i].z;
			sum3++;
			book[i]=1;
		}
	}
	INIT2();
}

int ans[MAXN<<2];
#define leftson cur<<1
#define rightson cur<<1|1
#define mid ((l+r)>>1)
#define push_up ans[cur]=max(ans[leftson],ans[rightson])
int ww[MAXN];
void build(int cur,int l,int r)
{
	if (l==r)
	{
		ans[cur]=ww[l];
		return;
	}
	build(leftson,l,mid);
	build(rightson,mid+1,r);
	push_up;
}
int query(int ql,int qr,int cur,int l,int r)
{
	if (ql<=l&&r<=qr) return ans[cur];
	int answ=0;
	if (ql<=mid) answ=query(ql,qr,leftson,l,mid);
	if (qr>mid) answ=max(answ,query(ql,qr,rightson,mid+1,r));
	return answ;
}
int son[MAXN],dep[MAXN],top[MAXN],siz[MAXN],id[MAXN],cnt=0;
void dfs1(int x)
{
	siz[x]=1;
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (y==fa[x]) continue;
		fa[y]=x;
		dep[y]=dep[x]+1;
		dfs1(y);
		siz[x]+=siz[y];
		if (siz[y]>siz[son[x]]) son[x]=y;
	}
}
void dfs2(int x,int tp)
{
	id[x]=++cnt;
	top[x]=tp;
	if (!son[x]) return;
	dfs2(son[x],tp);
	for (int i=h[x],y;i;i=e[i].nex)
	{
		y=e[i].to;
		if (y==fa[x]) continue;
		if (y==son[x]) { ww[id[son[x]]]=e[i].w; continue; }
		dfs2(y,y);
		ww[id[y]]=e[i].w;
	}
}
inline int query_tree(int x,int y)
{
	int answ=0;
	while (top[x]!=top[y])
	{
		if (dep[top[x]]<dep[top[y]]) swap(x,y);
		answ=max(answ,query(id[top[x]],id[x],1,1,n));
		x=fa[top[x]];
	}
	if (dep[x]>dep[y]) swap(x,y);
	return max(answ,query(id[x]+1,id[y],1,1,n));
}

int main()
{
	scanf("%d%d%lld",&n,&m,&X);
	for (int i=1;i<=m;i++) scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
	MST();
//	printf("MST:%lld\n",mst);
	int sum1=0,sum2=0;
	if (mst>X) { printf("0\n"); return 0; }
	dfs1(1);
	dfs2(1,1);
	build(1,1,n);
	for (int i=1,W;i<=m;i++)
	{
		if (book[i]) continue;
		W=query_tree(a[i].x,a[i].y);
//		printf("W:%d %d\n",a[i].z,W);
		if (a[i].z-W==X-mst) sum1++;
		else if (a[i].z-W>X-mst) sum2++;
	}
//	printf("sum1:%d sum2:%d sum3:%d\n",sum1,sum2,sum3);
	if (mst==X) printf("%lld\n",(power(2,sum2)*((power(2,sum1+sum3)-2+mod)%mod))%mod);
	else printf("%lld\n",((power(2,sum2)*((2*power(2,sum1)-2+mod)%mod))%mod)%mod);
	return 0;
}
/*
8 10
48
4 6 10
8 4 11
5 8 8
1 8 10
3 8 128773450
7 8 10
4 2 4
3 4 1
3 1 13
5 2 2
*/