局部异常因子（Local Outlier Factor, LOF）算法详解及实验

　　局部异常因子（Local Outlier Factor, LOF）通过计算样本点的局部相对密度来衡量这个样本点的异常情况，可以算是一类无监督学习算法。下面首先对算法的进行介绍，然后进行实验。

LOF算法

　　下面介绍LOF算法的每个概念，以样本点集合中的样本点$P$为例。下面的概念名称中都加了一个k-，实际上部分名称原文没有加，但是感觉这样更严谨一些。

　　k-邻近距离（k-distance）：样本点$P$与其最近的第$k$个样本点之间的距离，表示为$d_k(P)$。其中距离可以用各种方式度量，通常使用欧氏距离。

　　k-距离邻域：以$P$为圆心，$d_k(P)$为半径的邻域，表示为$N_k(P)$。

　　k-可达距离：$P$到某个样本点$O$的k-可达距离，取$d_k(O)$或$P$与$O$之间距离的较大值，表示为

$reach\_dist_k(P,O)=\max\{d_k(O),d(P,O)\}$

　　也就是说，如果$P$在$N_k(O)$内部，$reach\_dist_k(P,O)$取$O$的k-邻近距离$d_k(O)$，在$N_k(O)$外部则取$P$与$O$之间距离$d(P,O)$。需要注意k-可达距离不是对称的。

　　k-局部可达密度（local reachability density, lrd）：$P$的k-局部可达密度表示为

$\displaystyle lrd_k(P)=\left(\frac{\sum\limits_{O\in N_k(P)}reach\_dist_k(P,O)}{|N_k(P)|}\right)^{-1}$

　　括号内，分子计算了$P$到其k-距离邻域内所有样本点$O$的k-可达距离之和，然后除以$P$的k-距离邻域内部的样本点个数进行平均。再加一个倒数，表示为密度，即$P$到每个点的平均距离越小，密度越大。可以推理出，如果$P$在所有$O$的k-邻域内部，其局部可达密度即为

$\displaystyle lrd_k(P)=\left(\frac{\sum\limits_{O\in N_k(P)}d_k(O)}{|N_k(P)|}\right)^{-1}$

　　可以看出，如果$P$是一个离群点，那么它不太可能存在于$N_k(P)$中各点的k-距离邻域内，从而导致其局部可达密度偏小；如果$P$不是离群点，其局部可达密度最大取为上式。

　　实际上我有点奇怪为什么要用一个最大值来将距离作一个限制，也就是使用k-可达距离，而不是直接使用距离，即定义局部密度为下式

$\displaystyle ld_k(P)=\left(\frac{\sum\limits_{O\in N_k(P)}d(O,P)}{|N_k(P)|}\right)^{-1}$

　　k-局部异常因子（Local Outlier Factor, LOF）：$P$的k-局部异常因子表示为

$\displaystyle LOF_k(P)=\frac{\frac{1}{|N_k(P)|}\sum\limits_{O\in N_k(P)}lrd_k(O)}{lrd_k(P)}$

　　从直觉上理解：当$LOF_k(P)\le1$时，表明$P$处密度比其周围点大或相当，则$P$是内点；当$LOF_k(P)>1$时，表明$P$处密度比其周围点小，可以判别为离群（异常）点。

实验

LOF算法实现

　　实验设置样本维度为2以便可视化。由于样本点只包含连续值，实验默认设置$|N_k(P)|=k$。设置$k=5$，并将阈值设为1.2，即将LOF大于1.2的样本点视作异常。函数定义、抽样、计算以及可视化代码如下。

#%% 定义函数
import torch
import matplotlib.pyplot as plt

#计算所有样本点[N, M]之间的距离，得到[N, N]
def get_dists(points:torch.Tensor):
  x = torch.sum(points**2, 1).reshape(-1, 1)
  y = torch.sum(points**2, 1).reshape(1, -1)
  dists = x + y - 2 * torch.mm(points, points.permute(1,0))
  #数值计算问题，防止对角线小于0
  dists = dists - torch.diag_embed(torch.diag(dists))
  return torch.sqrt(dists)

#计算所有样本点到其k-邻域点的k-可达距离
def get_LOFs(dists:torch.Tensor, k):
  #距离排序，获取所有样本点的k-临近距离
  sorted_dists, sorted_inds = torch.sort(dists, 1, descending=False)
  k_dists = sorted_dists[:, k]
  neighbor_inds = sorted_inds[:, 1:k+1].reshape(-1)
  neighbor_k_dists = k_dists[neighbor_inds].reshape(-1, k)
  neighbor_k_reach_dists = torch.max(neighbor_k_dists, dists[:, 1:k+1])
  lrds = (neighbor_k_reach_dists.sum(1)/k)**-1
  neighbor_lrds = lrds[neighbor_inds].reshape(-1, k)
  LOFs = neighbor_lrds.sum(1)/k/lrds
  return LOFs

#%% 随机生成聚集点和异常点
from torch.distributions import MultivariateNormal
torch.manual_seed(0)

crowd_mu_covs = [
  [[0.0, 0.0], [[1.0, 0.0], [0.0, 2.0]], 10],
  [[-10.0, -1.0], [[2.0, 0.8], [0.8, 2.0]], 10],
  [[-10.0, -20.0], [[5.0, -2], [-2, 3.0]], 50],
  [[5.0, -10.0], [[5.0, -2], [-2, 3.0]], 50],
  [[-3.0, -10.0], [[5.0, -2], [-2, 3.0]], 50],
  [[-13.0, -10.0], [[0.3, -0.1], [-0.1, 0.5]], 10],
  [[-4.0, -10.0], [[0.3, -0.1], [-0.1, 0.1]], 100],
]#正态分布点的均值和方差
outliers = [[5, 5.], [3, 4], [5, -3], [4, -30], [-2, -35], [-10, -35]] #异常点

points = []
for i in crowd_mu_covs:
  mu = torch.tensor(i[0])
  cov = torch.tensor(i[1])
  ps = MultivariateNormal(mu, cov).sample([i[2]]).to('cuda')
  points.append(ps)
for o in outliers:
  points.append(torch.tensor([o]).to('cuda'))
points = torch.cat(points)

#%% 计算LOFs并可视化可视化
k, threshold = 5, 1.2
dists = get_dists(points)
LOFs = get_LOFs(dists, k)
for i, p in enumerate(points.cpu().numpy()):
  shape, color = '.', 'black'
  if len(points) - i <= len(outliers):
    shape = '^'
    plt.annotate("%.2f"%LOFs[i].cpu().numpy(), (p[0], p[1]))
  if LOFs[i] > threshold:
    color = 'red'
    plt.annotate("%.2f"%LOFs[i].cpu().numpy(), (p[0], p[1]), color='blue')
  plt.plot(p[0], p[1], shape, color=color)
plt.show()

　　实验可视化结果如下图所示，其中红色点表示被标为异常的点，三角点表示实验设置的真实异常点。可以看出LOF的确能有效将异常离群点找出。但是，发现下面三个人眼看来非常离群的点的LOF值还不到1.5，比上面异常点的LOF低得多，这说明算法还有些不合理之处。

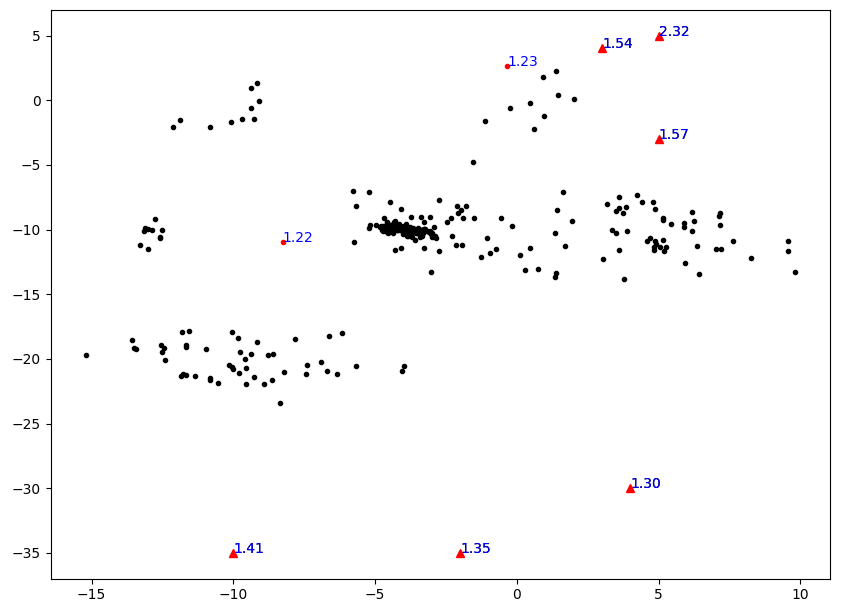
距离代替局部可达距离

　　根据前面的疑问，用距离代替局部可达距离进行相应实验。仅在get_LOFs函数处做了相关改动，并将阈值threshold改为2。代码如下。

#%% 定义函数
import torch
import matplotlib.pyplot as plt

#计算所有样本点[N, M]之间的距离，得到[N, N]
def get_dists(points:torch.Tensor):
  x = torch.sum(points**2, 1).reshape(-1, 1)
  y = torch.sum(points**2, 1).reshape(1, -1)
  dists = x + y - 2 * torch.mm(points, points.permute(1,0))
  #数值计算问题，防止对角线小于0
  dists = dists - torch.diag_embed(torch.diag(dists))
  return torch.sqrt(dists)

#计算所有样本点到其k-邻域点的k-可达距离
def get_LOFs(dists:torch.Tensor, k):
  #距离排序，获取所有样本点的k-临近距离
  sorted_dists, sorted_inds = torch.sort(dists, 1, descending=False)
  densities = (sorted_dists[:, 1:k+1].sum(1)/k)**-1
  neighbor_inds = sorted_inds[:, 1:k+1].reshape(-1)
  neighbor_densities = densities[neighbor_inds].reshape(-1, k)
  LOFs = neighbor_densities.sum(1)/k/densities
  return LOFs

#%% 随机生成聚集点和异常点
from torch.distributions import MultivariateNormal
torch.manual_seed(0)

crowd_mu_covs = [
  [[0.0, 0.0], [[1.0, 0.0], [0.0, 2.0]], 10],
  [[-10.0, -1.0], [[2.0, 0.8], [0.8, 2.0]], 10],
  [[-10.0, -20.0], [[5.0, -2], [-2, 3.0]], 50],
  [[5.0, -10.0], [[5.0, -2], [-2, 3.0]], 50],
  [[-3.0, -10.0], [[5.0, -2], [-2, 3.0]], 50],
  [[-13.0, -10.0], [[0.3, -0.1], [-0.1, 0.5]], 10],
  [[-4.0, -10.0], [[0.3, -0.1], [-0.1, 0.1]], 100],
]#正态分布点的均值和方差
outliers = [[5, 5.], [3, 4], [5, -3], [4, -30], [-2, -35], [-10, -35]] #异常点

points = []
for i in crowd_mu_covs:
  mu = torch.tensor(i[0])
  cov = torch.tensor(i[1])
  ps = MultivariateNormal(mu, cov).sample([i[2]]).to('cuda')
  points.append(ps)
for o in outliers:
  points.append(torch.tensor([o]).to('cuda'))
points = torch.cat(points)

#%% 计算LOFs并可视化可视化
k, threshold = 5, 2
dists = get_dists(points)
LOFs = get_LOFs(dists, k)
for i, p in enumerate(points.cpu().numpy()):
  shape, color = '.', 'black'
  if len(points) - i <= len(outliers):
    shape = '^'
    plt.annotate("%.2f"%LOFs[i].cpu().numpy(), (p[0], p[1]))
  if LOFs[i] > threshold:
    color = 'red'
    plt.annotate("%.2f"%LOFs[i].cpu().numpy(), (p[0], p[1]), color='blue')
  plt.plot(p[0], p[1], shape, color=color)
plt.show()

　　可视化结果如下图所示。

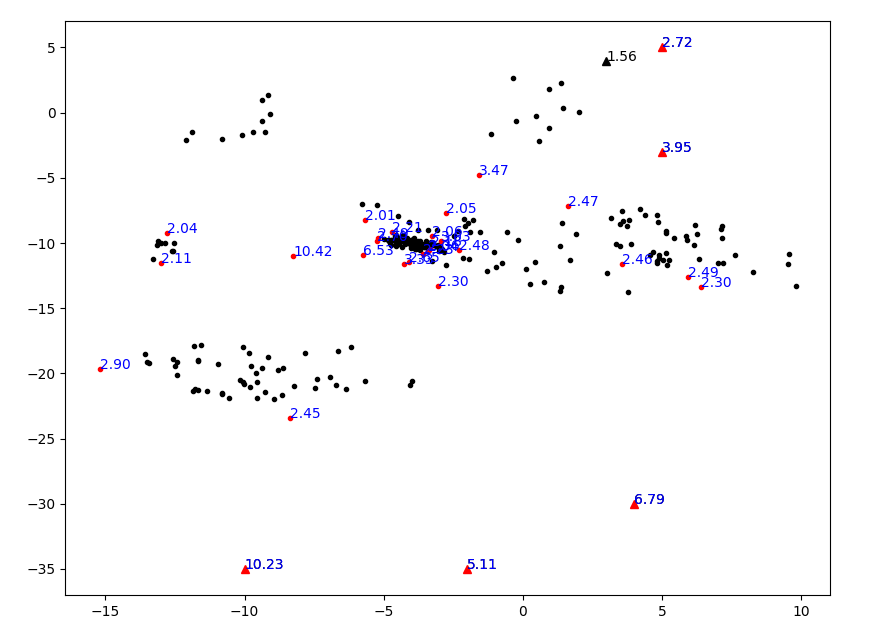
　　部分离群点的确能被有效找出，但是看起来似乎这个算法对“相对”的概念太显著了，导致一个聚集的点群里面也有很多不是那么聚集的点被划分为离群点。看来用距离代替局部可达距离是不行的。但是如何从理论上来解释，本文不再作深究，欢迎前来讨论。