[排序算法] 2路插入排序 (C++)

前言

本文章是建立在 插入排序 的基础上写的，如果还有不懂 插入排序 的童鞋先停下脚步，可以先看看这里~ 直接/折半插入排序

---

2路插入排序解释

在 插入排序 中，当待插入元素需要插入的位置位于当前有序序列的首位时，我们需要进行更多的元素后移操作。过多的交换操作消耗了很多时间，因此可以着眼于减少交换次数这个方面，提高 插入排序 的效率。这就是为什么出现了 2路插入排序。

2路插入排序 是对 插入排序 的进一步改进，它是通过在首尾两路同时进行插入操作，来减少插入过程中移动的次数。

那么具体如何实现呢？

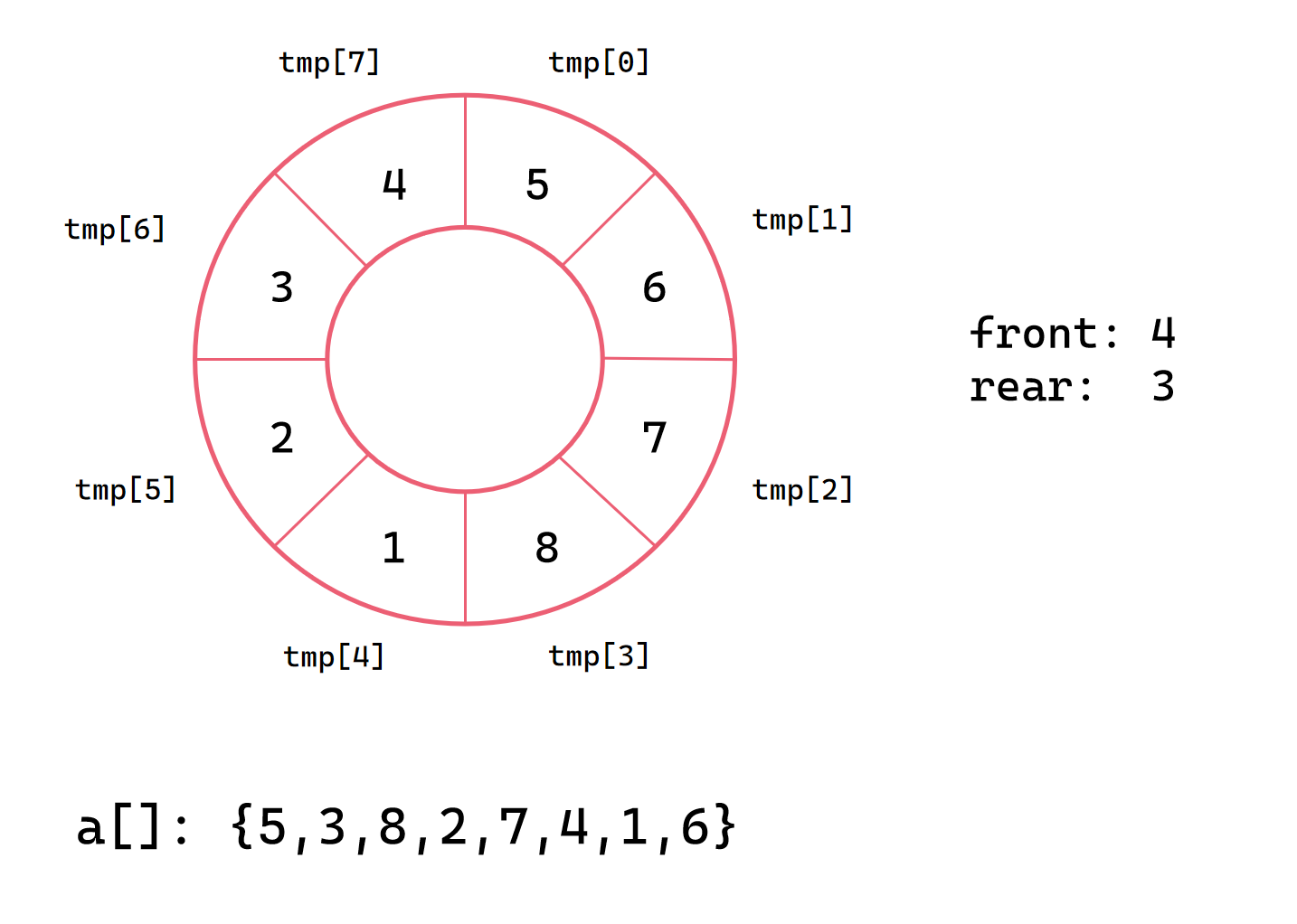
我们用一个临时数组 tmp 来存储当前已排序序列，每次插入元素后有序序列的长度都会 +1。因为要进行首尾两路的插入操作，我们需要将临时数组 tmp 作为一个循环数组来处理，同时定义 front 和 rear 来标记当前有序序列中的头尾。这是 2路插入排序 的核心。

---

2路插入排序动态演示

我们需要一个循环数组 tmp，因此有了下图

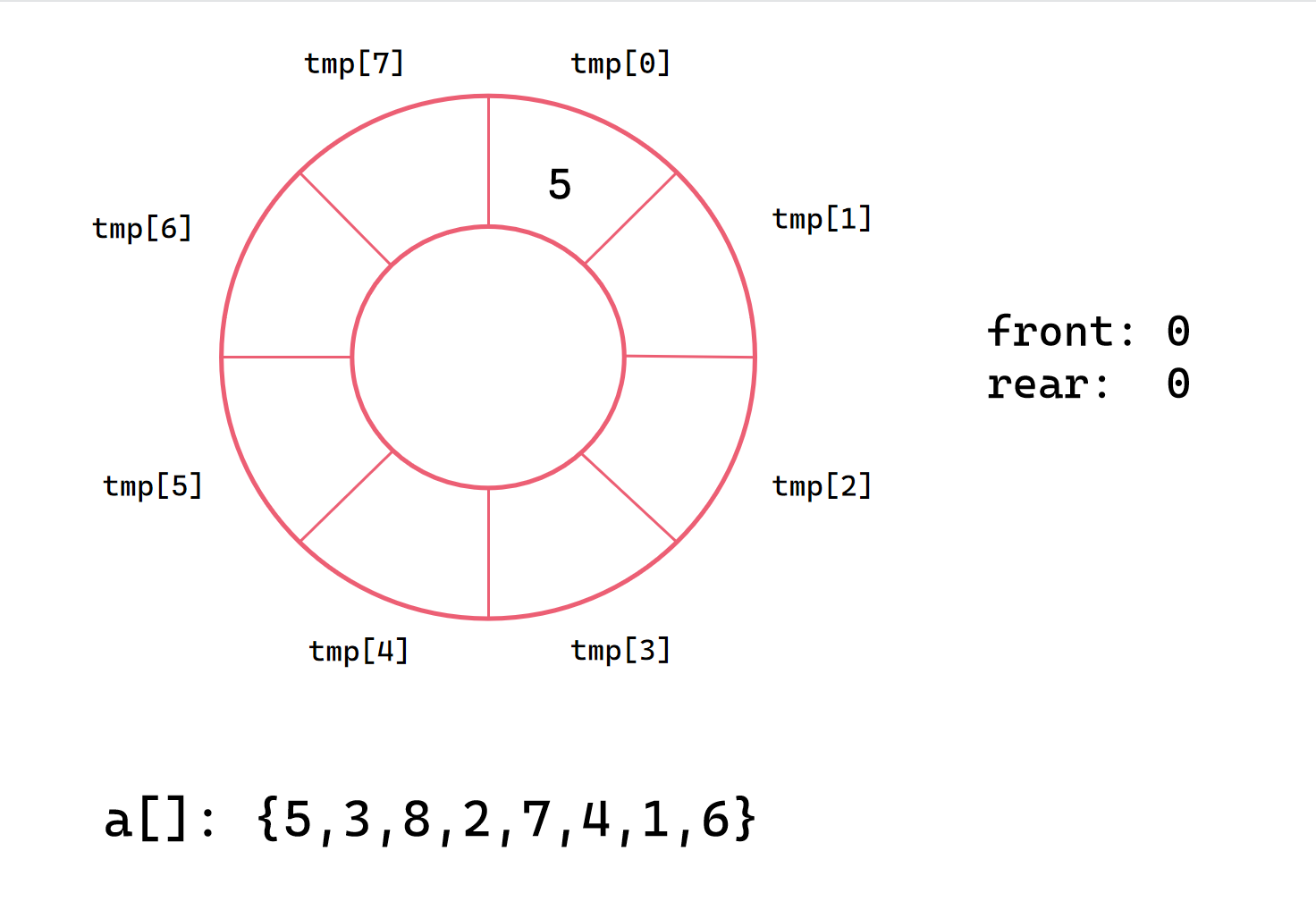
我们以 [5, 3, 8, 2, 7, 4, 1, 6] 为例进行动态演示

第一次插入

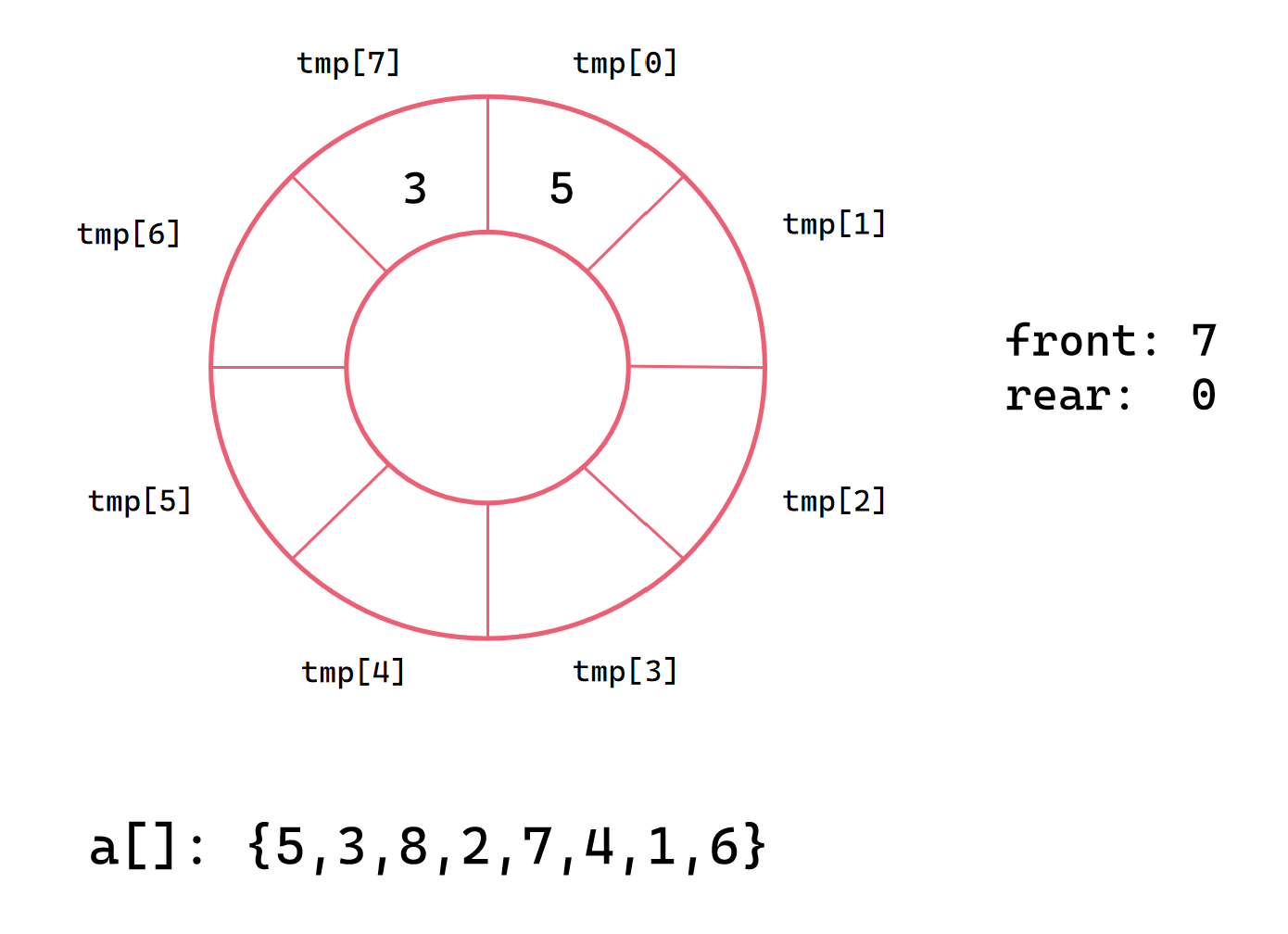
第二次插入

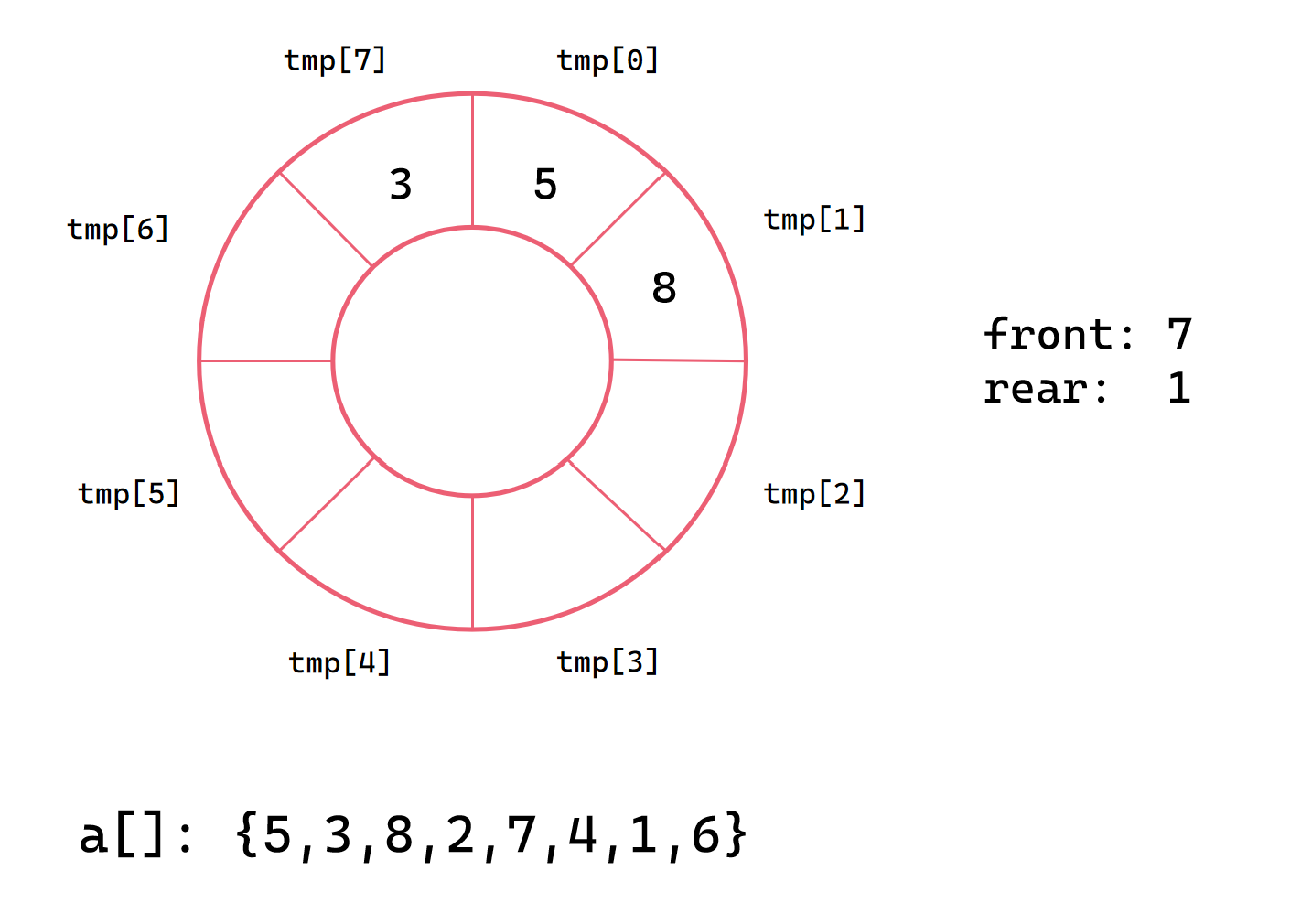
第三次插入

第四次插入

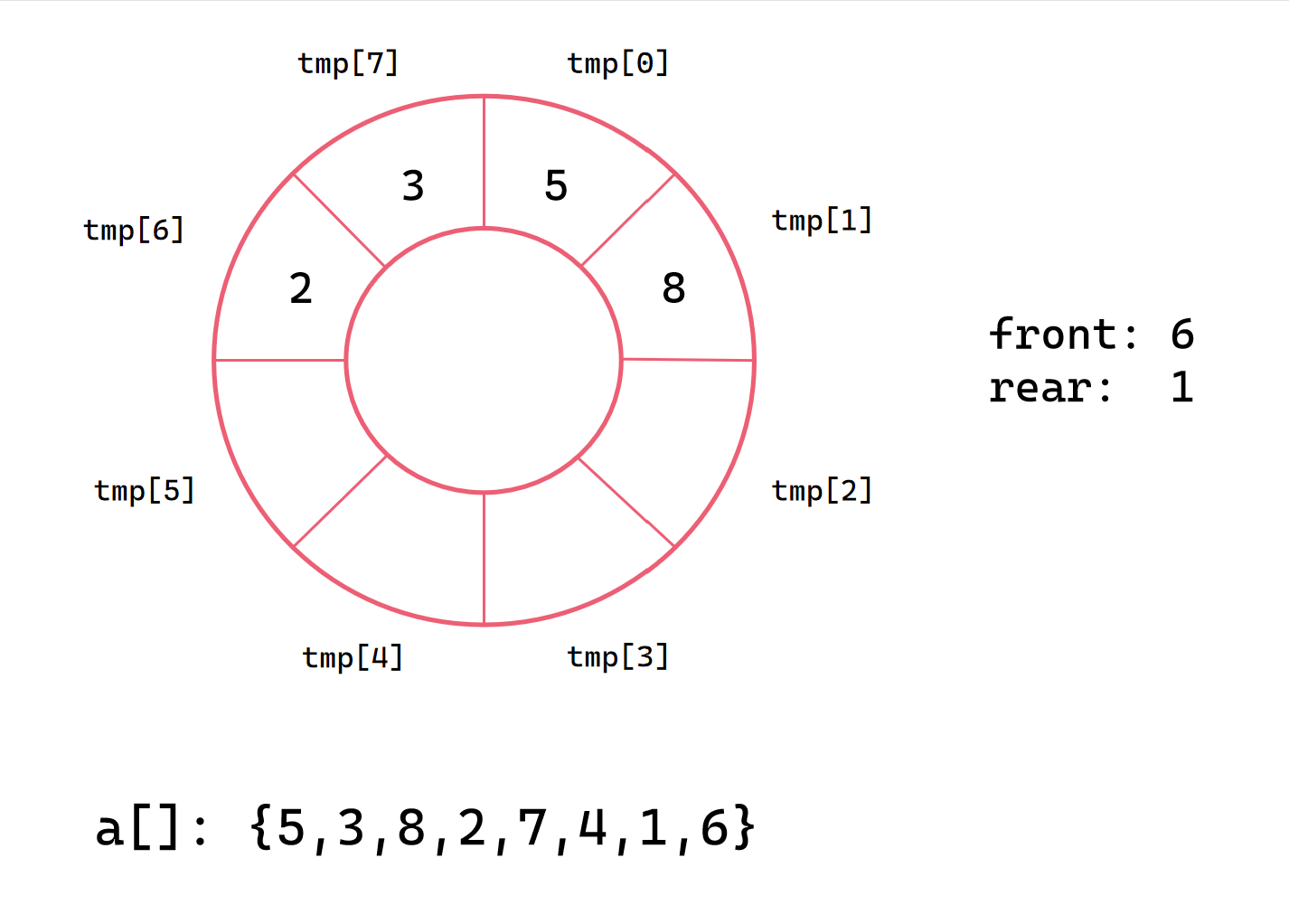
第五次插入

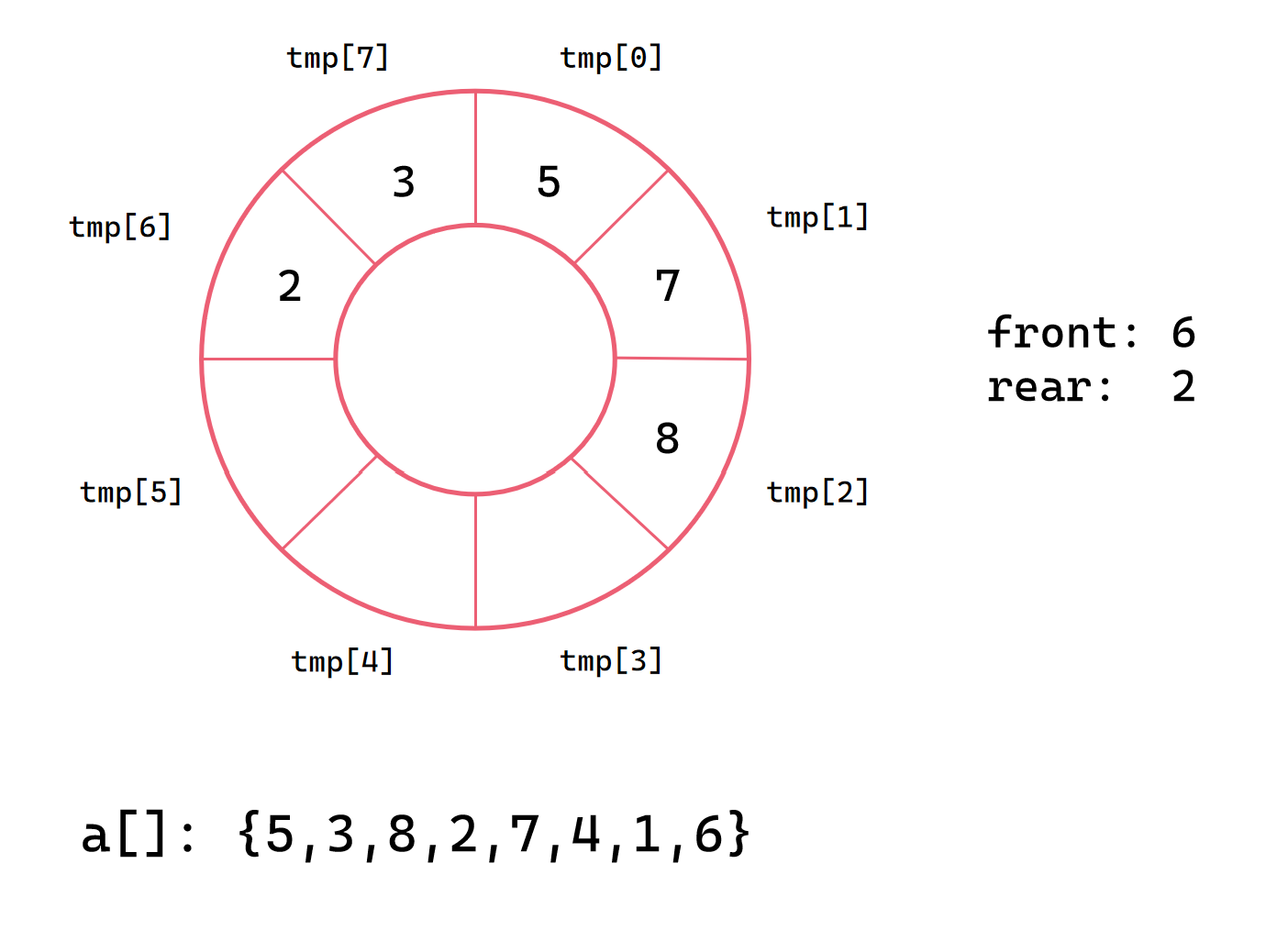
第六次插入

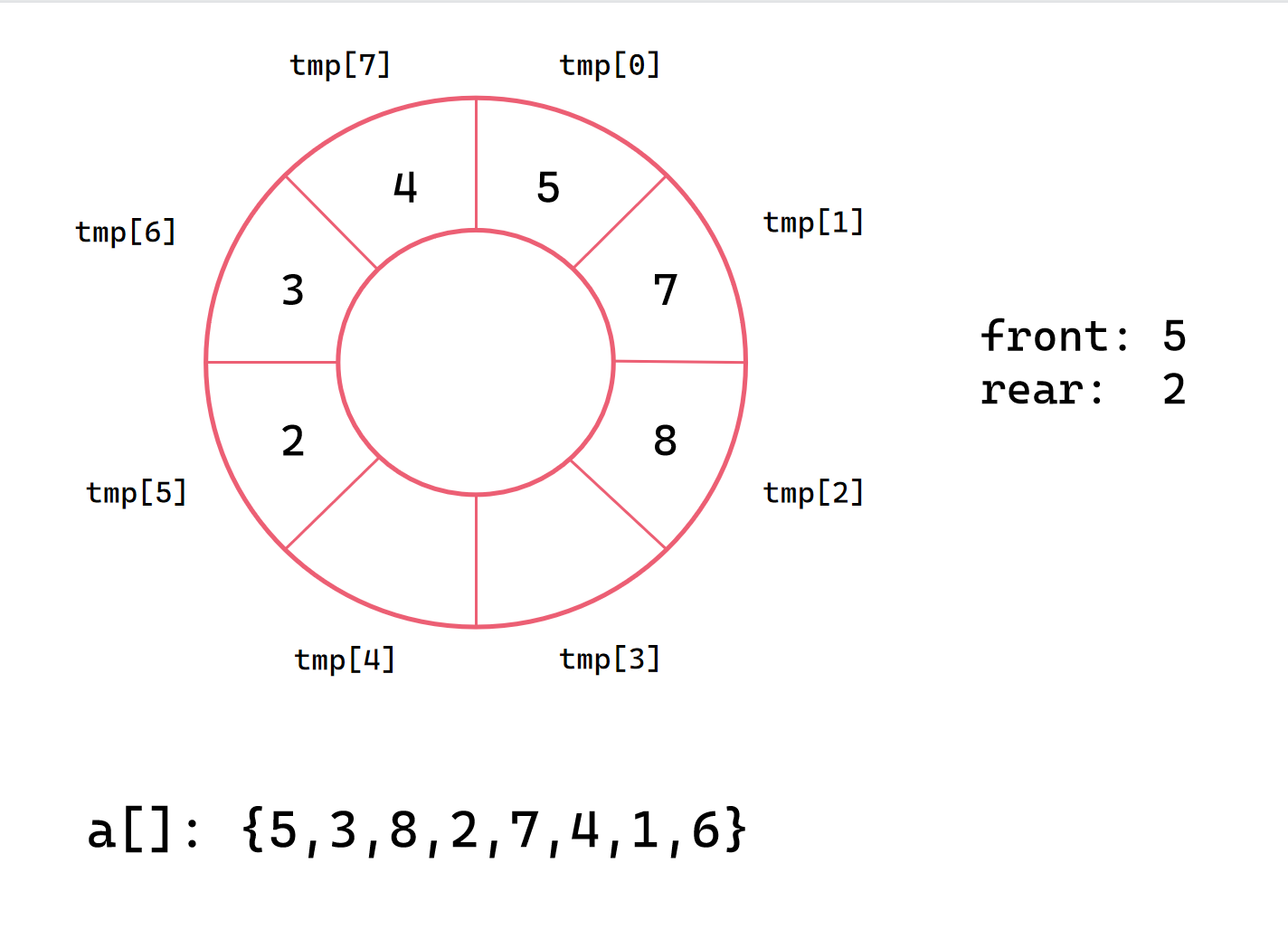
第七次插入

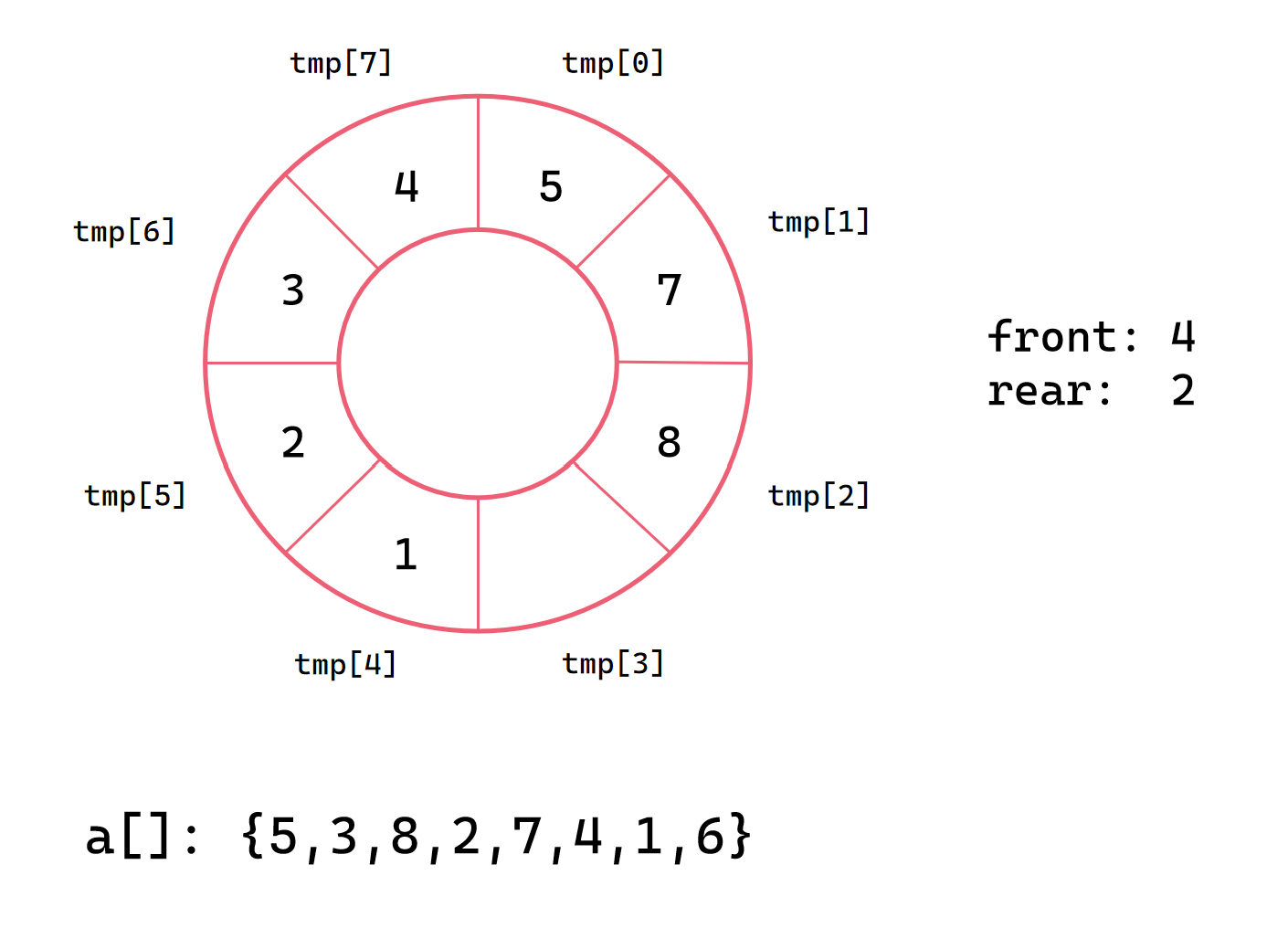
第八次插入

---

2路插入排序核心代码

void TwoInsertSort(int a[], int n){
    int *tmp = new int[n];     //临时数组
    int front = 0, rear = 0;   //记录当前tmp数组中最大值和最小值的位置
    tmp[0] = a[0];             //初始化tmp

    for(int i = 1; i < n; i++){
        int key = a[i];
	//如果当前插入的元素比最小的元素更小
	if(key < tmp[front]){
            front = (front - 1 + n) % n;
	    tmp[front] = key;
	}
	//如果当前插入元素比最大元素更大
	else if(key > tmp[rear]){
	    rear = (rear + 1 + n) % n;
	    tmp[rear] = key;
	}
	//如果在当前最小和最大之间
	else{
	    int k = (rear + n) % n;
	    //将比当前插入值key大的进行后移
	    while(tmp[(k + n) % n] > key){
		tmp[(k + 1 + n) % n] = tmp[(k + n) % n];
		k = (k - 1 + n) % n;
	    }

	    tmp[(k + 1 + n) % n] = key; //当前插入值放到合适位置
	    rear = (rear + 1 + n) % n;  //更新最大值位置(有序序列长度+1)
	}
    }

    //复制临时数组到原数组中
    for(int k = 0; k < n; k++)
        a[k] = tmp[(front + k) % n];
    delete[] tmp;
}

---

完整程序源代码

#include<iostream>
#include<ctime>
using namespace std;

//临时数组作为循环数组操作
void TwoInsertSort(int a[], int n){
    int *tmp = new int[n];     //临时数组
    int front = 0, rear = 0;   //记录当前tmp数组中最大值和最小值的位置
    tmp[0] = a[0];             //初始化tmp

    for(int i = 1; i < n; i++){
	int key = a[i];
	//如果当前插入的元素比最小的元素更小
	if(key < tmp[front]){
	    front = (front - 1 + n) % n;
	    tmp[front] = key;
	}
	//如果当前插入元素比最大元素更大
	else if(key > tmp[rear]){
	    rear = (rear + 1 + n) % n;
	    tmp[rear] = key;
	}
	//如果在当前最小和最大之间
	else{
	    int k = (rear + n) % n;
	    //将比当前插入值key大的进行后移
	    while(tmp[(k + n) % n] > key){
		tmp[(k + 1 + n) % n] = tmp[(k + n) % n];
		k = (k - 1 + n) % n;
	    }

	    tmp[(k + 1 + n) % n] = key; //当前插入值放到合适位置
	    rear = (rear + 1 + n) % n;  //更新最大值位置(有序序列长度+1)
	}
    }

    //复制临时数组到原数组中
    for(int k = 0; k < n; k++)
	a[k] = tmp[(front + k) % n];
    delete[] tmp;
}

void show(int *a, int n){
    for(int i = 0; i < n; i++)
	cout<<*(a + i)<<" ";
    cout<<endl;
}

main(){
    int a[50];
    srand((int)time(0));
    int k = 0;
    while(k < 50)
	a[k++] = rand() % 100 + 1;   //数字范围[1,100]

    show(a, 50);

    TwoInsertSort(a, 50);

    cout<<endl<<endl;
    show(a, 50);
}

---

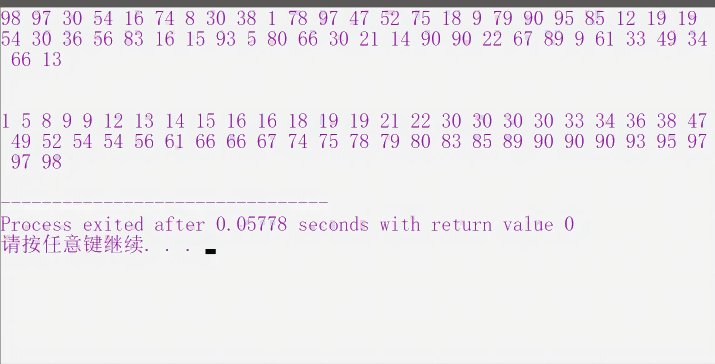
程序运行结果图