Machine Learning - week 4 - Non-linear Hypotheses

为什么计算机图像识别很难呢？因为我们看到的是汽车，而计算机看到的是表示颜色的 RGB 数值。计算机需要根据这些数值来判断。

如果图片是 50 * 50 像素，那么一共有 2500 个像素点。如果是 Quadratic features，那么是 x_i, x_j 的组合有 2500 + 2499 + ... + 1 约为 300 百万个。

Neurons and the Brain

大脑可以学习很多种算法，但是程序是固定的（出生到死亡都没有人修改你的大脑程序）。通过计算机模仿大脑的这种学习，这样，就不需要编写很多算法了，只需要编写少量的几种，然后让它们去学习就可以了。

Neural Networks

s_j+1 = θ_j * s_j

当前层 = θ * 前一层

这个计算 h_θ(x) 的过程，也称为向前传播。我们从输入的激励层开始，然后向前传播给隐藏层并计算隐藏层的激励，然后继续向前传播直到计算出输出层的激励。

通过隐藏层计算，就能够得到更加复杂的训练数据，且复杂程度是加强的。

将 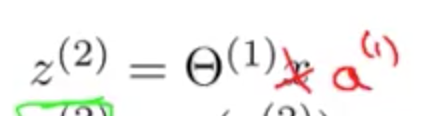，那么 ，也就可以用向量计算了。

Applications

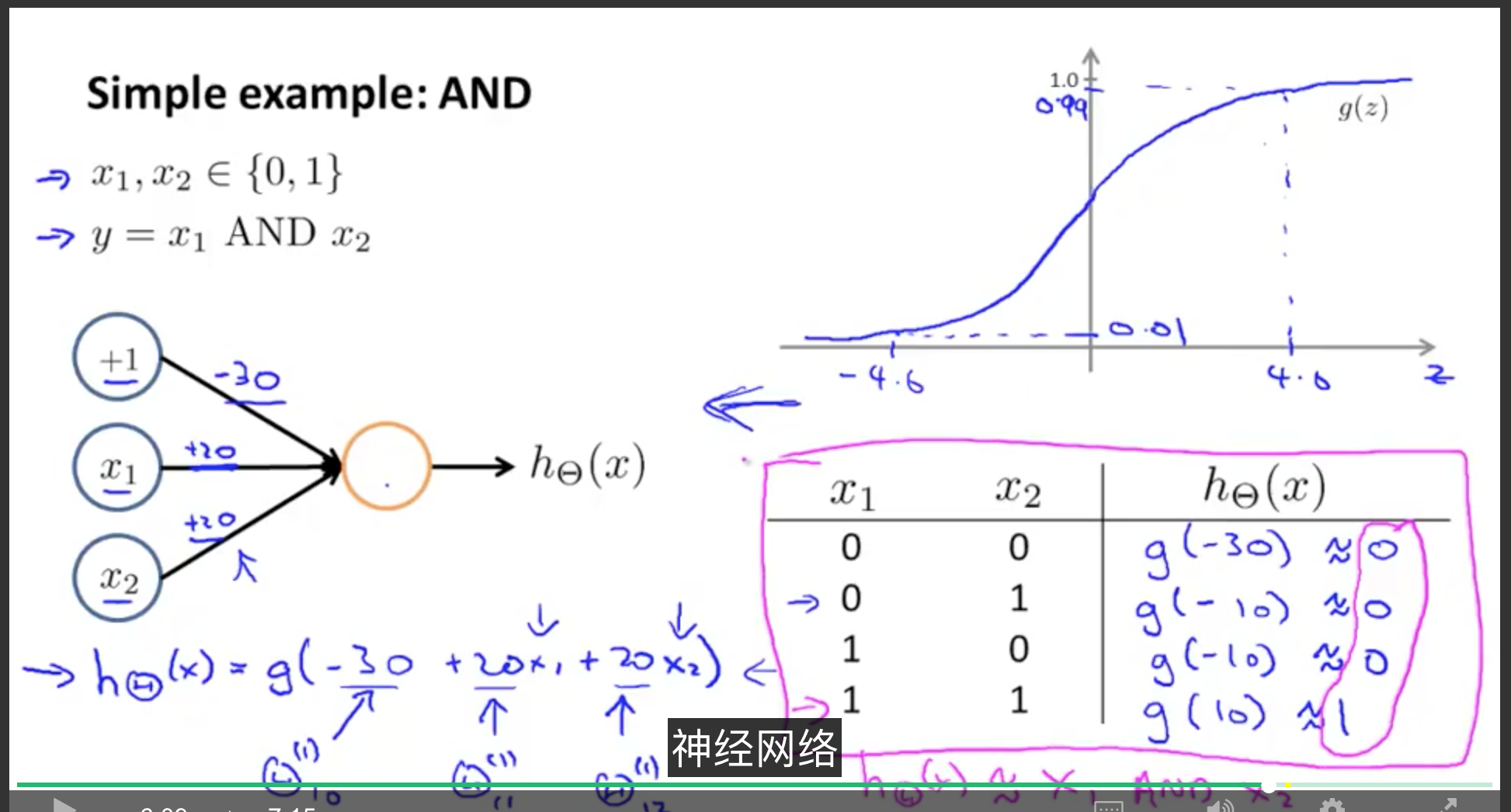
通过神经网络实现 AND 函数

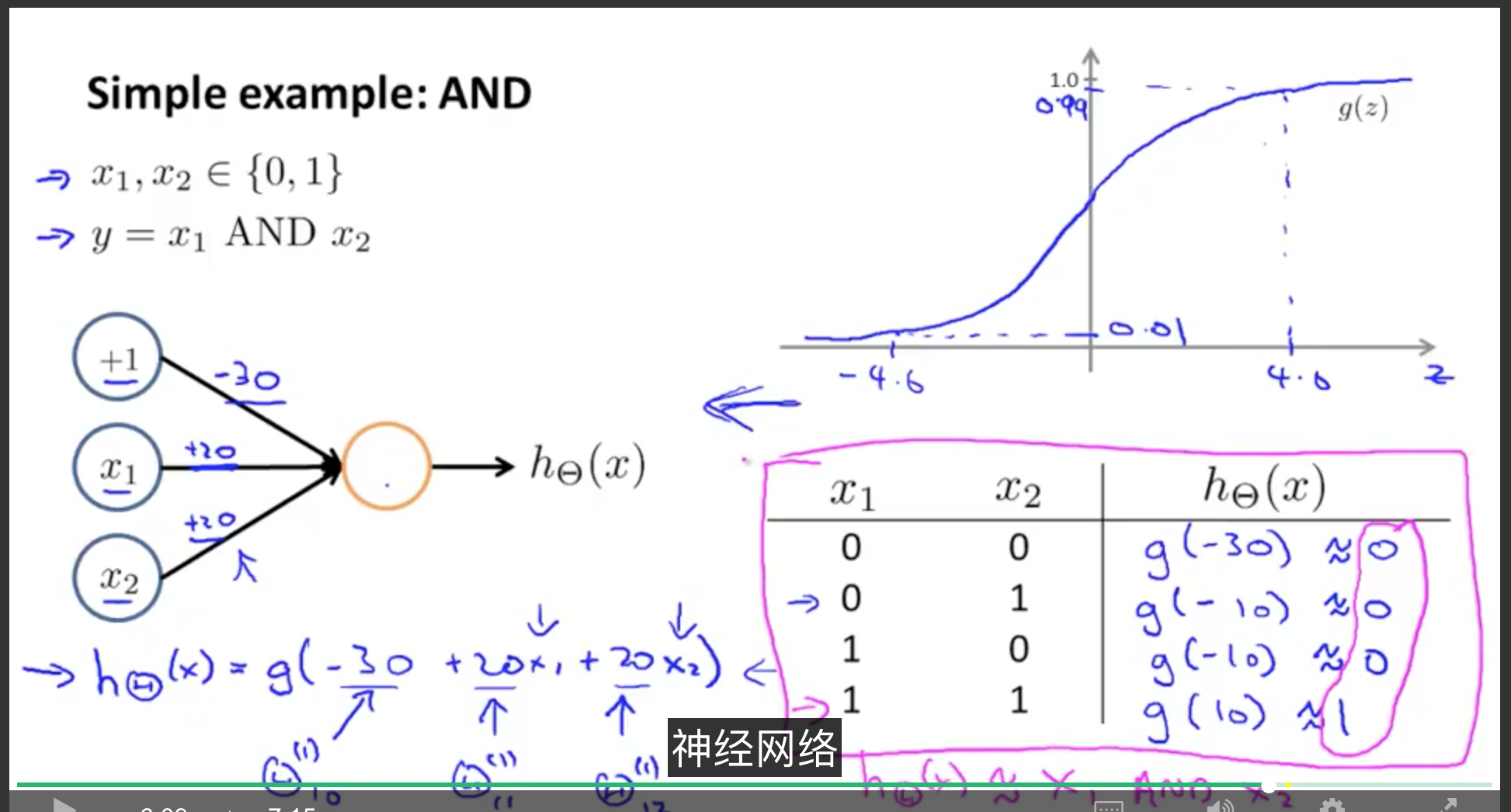针对训练集实现的效果是一样的，并且能够进行预测。

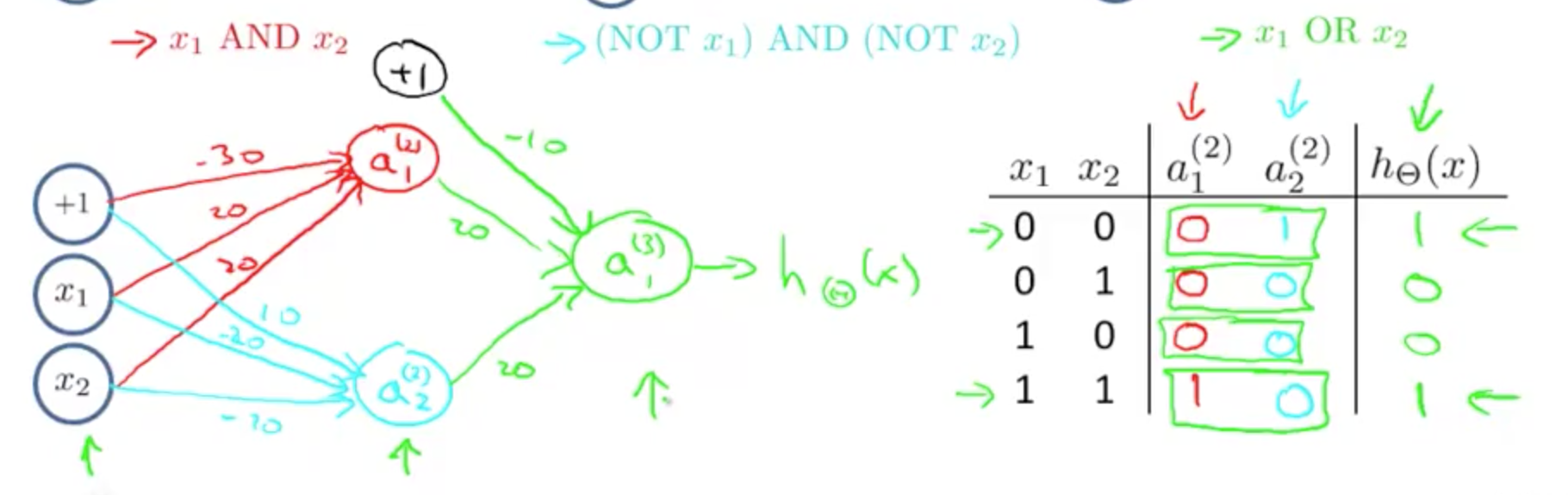
实现非线性函数

将三个组合成一个

组合后各层的计算方式

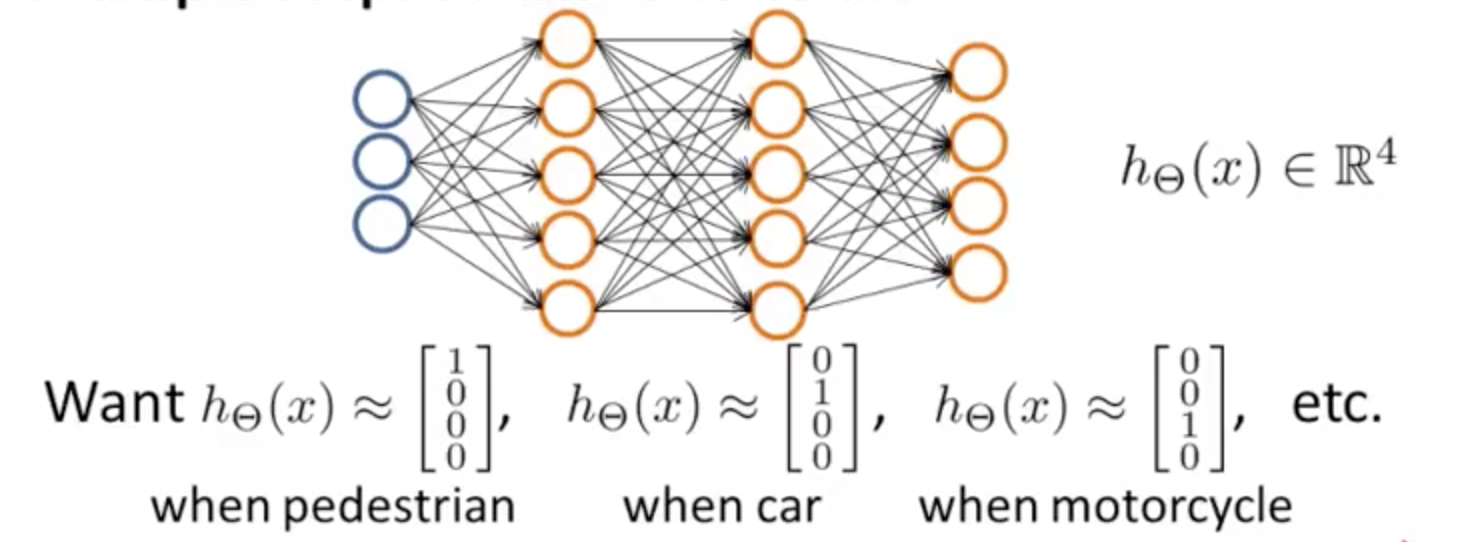
多类别分类

同样使用 one-vs-all 的方式。

对于一组 features（ X(j:) ），预测出一组（features 个数个）值，取最大值表示最有可能的预测结果。

求 costFunction 的时候，使用 y == 类别，除了目标类别，其他类别都是 0。