ML技术 - 特征选择

1. 决策树中的特征选择

　　分类决策树是一种描述对实例进行分类的树型结构，决策树学习本质上就是从训练数据集中归纳出一组分类规则，而二叉决策树类似于if-else规则。决策树的构建也是非常的简单，首先依据某种特征选择手段对每一特征对分类的贡献性大小排序，然后从根节点开始依次取出剩下特征中对分类贡献最大的特征，用其作为当前节点的分类准则，进一步构造其叶子结点，然后重复此过程，直到特征用光或满足了预先设定的要求终止决策树的构建。由此可见，特征选择作为决策树构建的核心技术而存在，那么下面我们就来讨论一下决策树中常用的特征选择技术有哪些：

1.1 信息增益与信息增益比

　　一个特征所包含的信息量可以通过看这个特征对整体稳定性的影响大小来确定。举个例子，

　　　　假设我问你：今年冬天会下雪？

　　　　你会反问：你说的哪呀？南方和北方会一样么？你说的话一点信息量都没有！

　　　　我又问：海南，今年冬天会下雪么？

　　　　你会说：那肯定不会下呀，气温都到不了0下！

从这对话中我们看到，就冬天会不会下雪这个问题开始时会有两个等可能的判断，这时候是最让我们摸不着头脑的，如果我们接着为其添加一个地域的约束也就是上面的A，此时我们的问题就一下子明朗起来，可见地域信息为我们这个问题的判断提供了非常大的信息参考。除了地域这个特征，也许还有其他一些信息会影响我们对下雪这个问题的判断，那么在这个问题我们该如何比较中的各个特征的信息量大小呢？没错，就是信息增益。　信息增益衡量的是在得知某一特征A的信息后而使得类Y的不确定性减少的程度，公式如下：

　　　　　　　　

这里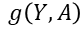，表示特征A对类别Y的信息增益，而随机事件的不确定性可以通过熵来衡量，故 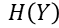表示类别Y的熵（不确定性），表示在得知特征A后类别Y的熵。可见信息增益是基于熵提出的！那么问题来了，熵如何衡量事件不确定性的呢？我们首先从公式说起：

　　　　　　　　

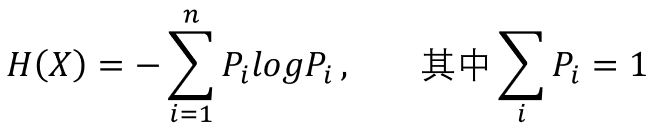
用拉格朗日乘子法，我们可以解得当 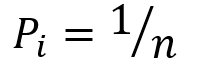时，熵是最大的（证明过程参见）。对于一次伯努利实验的结果其熵的分布满足：

　　

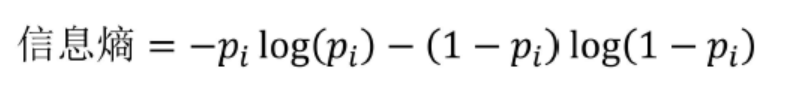
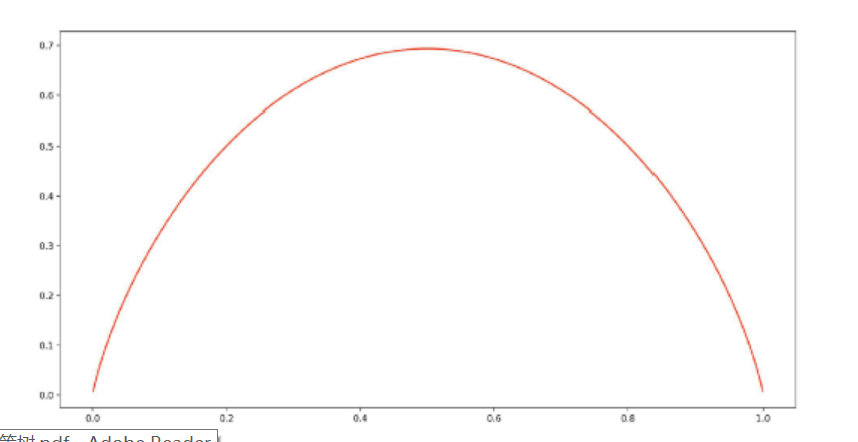
可见，在事件最不确定的时候，其熵值最大，也就是说熵是不确定性的单调递增函数。那么问题又来了，为什么熵的公式是这样的？具体参考可以参见知乎问答。

　　有时候信息增益并不能很好的度量两个特征哪个特征对分类的贡献大。借用一下李航老师统计学习方法中的贷款申请的例子：

　　　　

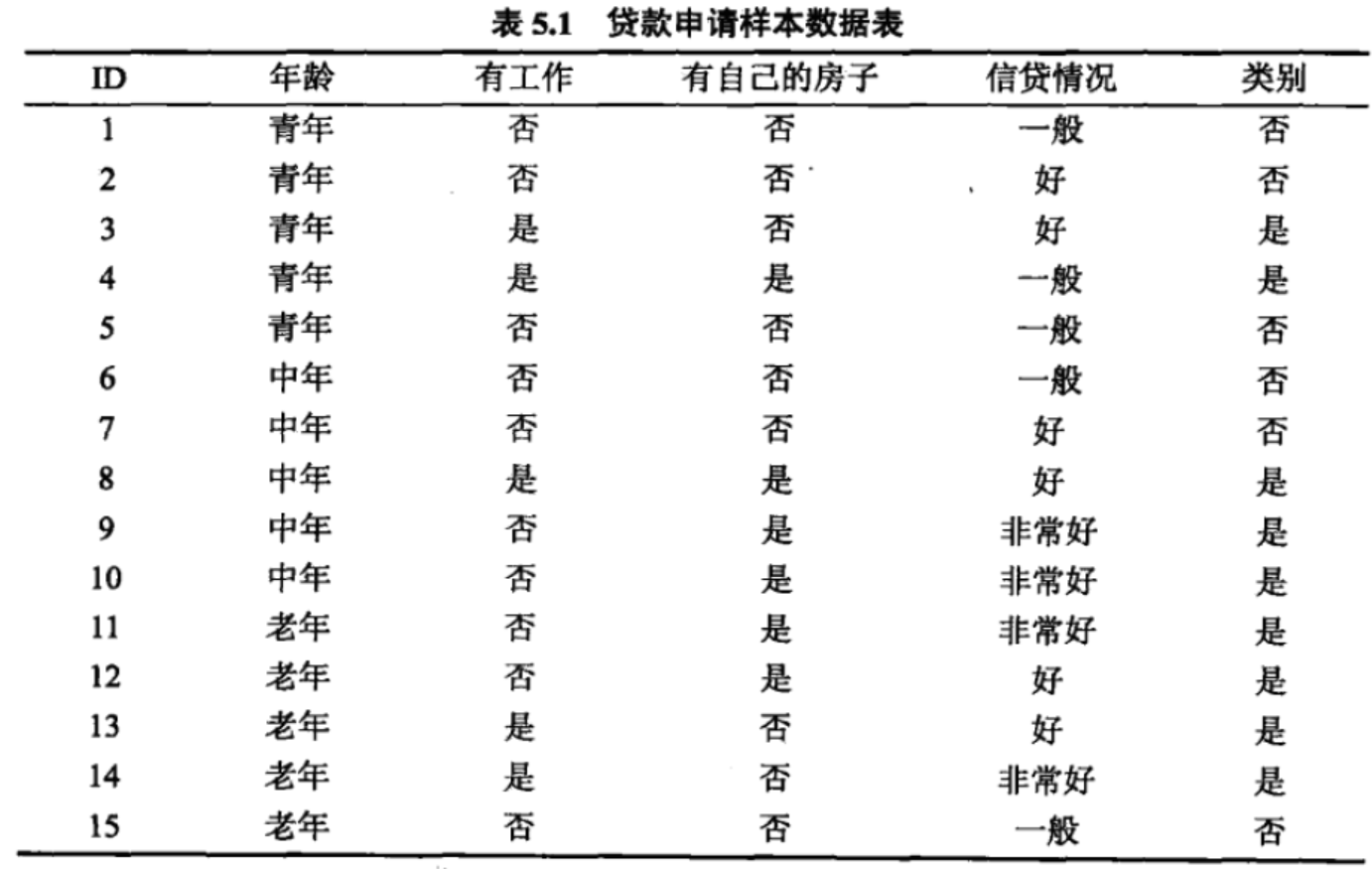
类别有6个“否”、9个“是”，那么数据集D的熵为：

　　　　

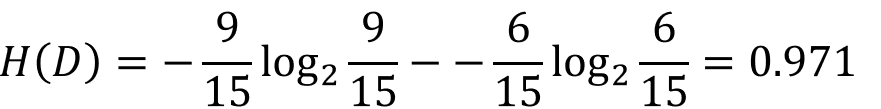
而对于四种特征它们的信息增益分别是：

　　　　

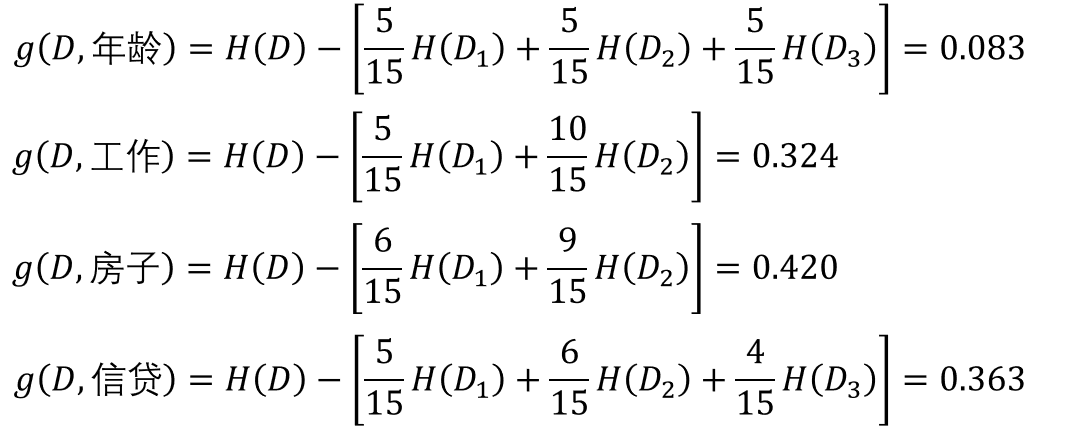
到这里看着似乎没什么问题，那么我们将创造一个问题，把ID也当成一个特征，看看它的信息增益是多少：

到这里我们发现了ID的信息增益最大呀！那ID就是最好的特征么？开玩笑吧！总的来说，信息增益倾向于选择特征取值多的特征，和上面的例子一样，把ID当作最好的特征，是不是很傻。所以为了克服它的这种缺陷，信息增益比就诞生了。信息增益比相当于对每个特征的信息增益加了一个权值，抵消了特征取值数对信息增益的影响，这样就把信息增益归一到同一量级，更加方便比较它们的大小。

　　特征A对于训练数据集D的信息增益比定义为：

　　　　，其中n为特征A的取值个数。

1.2 基尼系数

　　CART分类树中会用到基尼指数作为样本不确定性的度量，同熵代表的含义相同：基尼系数越大，代表了随机变量越不确定，也就是随机变量越随机。分类问题中，假设有K个类，样本属于第k类的概率为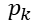，那么该概率分布的基尼指数为

　　　　　　

CART构造的是一颗二叉分类树，那么一般我们将一特征集切分成两部分，故得到在特征A给定的条件下，集合D的基尼指数定义为

　　　　　　

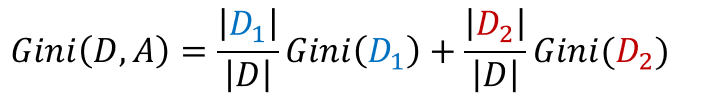
2. Sklearn中的特征选择

　　特征选择并不只是用于决策树的构建，特征选择也是机器学习中经常用到的一门技术。特征选择技术出现的原因是：我们要知道在一个机器学习任务中，并不是我们获取的所有特征都对模型构建有着积极的影响，即使都有积极的效益，我们可能也要权衡特征项数与建模效率之间的关系。而特征选择可以非常有效的解决这些问题。特征选择技术可以帮助我们筛选出对建模最有用的特征，把可有可无的特征项去除，不仅可以加速我们模型的训练，还可以有效清除噪声特征对模型的影响。下面将简单过一下sklearn中特征选择，然后选一些自己曾经见过的技术，研究一下它的用法：

2.1 基于卡方统计量的特征选择

　　what is 卡方检验统计量：卡方统计量是用于检验实际分布与理论分布配合程度，也可以说成统计样本的实际观测值与理论推断值之间的偏差程度的统计量。若卡方值越大，说明偏差越大，越不符合实际；而卡方值越小，说明偏差越小，越是符合实际情况；若卡方值为0，说明理论完全符合实际！下面是卡方统计量的公式：

　　　　　　

其中， 表示实际观测次数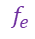，表示理论观测次数。因为卡方检验可以用于检测随机变量之间的依赖关系，因此我们可以用它来清除那些最有可能与类别不想关的特征，来减少噪音特征对分类的影响。

sklearn.feature_selection.chi2(X, y)
"""
参数
---
    X: 特征矩阵 （n_samples * n_features_in 维）
    y: 标签向量 （n_samples * 1 维）

返回值
---
    chi2：每个特征的卡方统计量（n_features * 1 维）
    pval ：每个特征的p-value （n_features * 1 维）

算法时间复杂度O(n_samples * n_features_in)
"""

2.2 基于方差分析的特征选择

　　方差是描述随机变量离散程度的统计量，其公式为：

　　　　　　　　

而分差分析基本思想认为不同特征对分类模型的贡献程度之所以不同，主要源自于各个特征在组内与组间离散程度存在差异，于是F-score就出现了:

　　　　　　　　

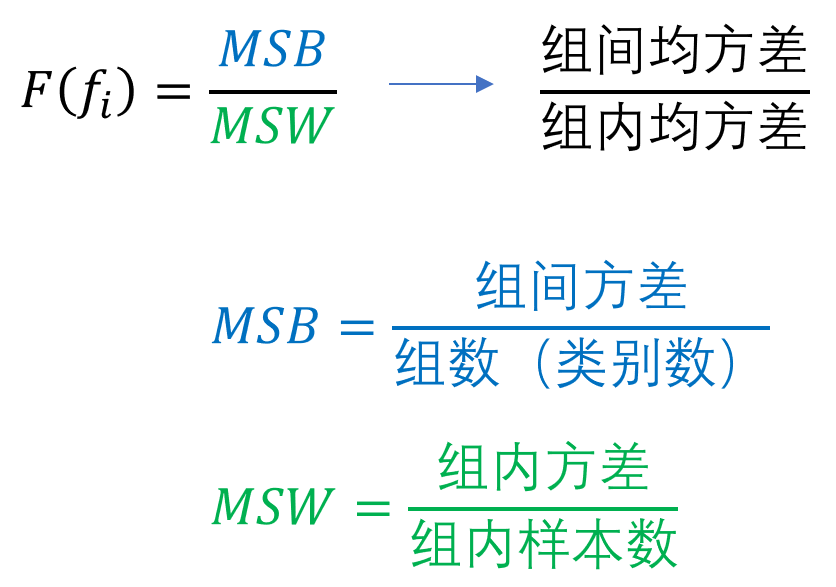
sklearn.feature_selection.f_classif(X, y)
"""
参数
---
    X: 特征矩阵 （n_samples * n_features_in 维）
    y: 标签向量 （n_samples * 1 维）

返回值
---
    F：每个特征的卡方统计量（n_features * 1 维）
    pval ：每个特征的p-value （n_features * 1 维）

算法时间复杂度O(n_samples * n_features_in)
"""