POJ-3020 Antenna Placement---二分图匹配&最小路径覆盖&建图

题目链接：

https://vjudge.net/problem/POJ-3020

题目大意：

一个n*m的方阵 一个雷达可覆盖两个*，一个*可与四周的一个*被覆盖，一个*可被多个雷达覆盖问至少需要多少雷达能把所有的*覆盖

解题思路：

把每个*城市编号，然后每相邻两个城市之间连线。这里求最少多少个雷达可以覆盖完*，就是二分图匹配中的最小路径覆盖数，但是这里的图的边是双向的。举个例子

o*o

**o

ooo

这里可以编号成

010

230

000

那么有边<1,3><3,1><2,3><3,2>

按照二分图匹配建图的方法，每个点拆分成两个点A1，A2，如果有边<A, B>在二分图中建立边<A1, B2>。

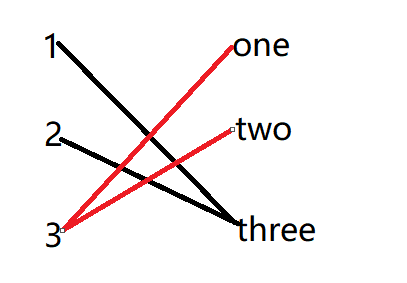
这里的特殊性在于1和3有边，3和1也有边，所以最后求出来的最大匹配需要除以2才是题目所需要的最大匹配

最小路径覆盖数 = 顶点数 - 最大匹配

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 typedef pair<int, int> Pair ;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn =  + ;
 int T, n, m, cases;
 vector<int>G[maxn];
 int cx[maxn], cy[maxn];
 bool vis[maxn];
 char Map[][];
 int cnt[][], tot;
 int dir[][] = {,,,,-,,,-};
 bool dfs(int u)
 {
     for(int i = ; i < G[u].size(); i++)
     {
         int v = G[u][i];
         if(!vis[v])
         {
             vis[v]  =;//加入增广路
             if(cy[v] == - || dfs(cy[v]))
             {
                 cx[u] = v;
                 cy[v] = u;
                 return ;
             }
         }
     }
     return ;
 }

 int maxmatch()
 {
     int ans = ;
     memset(cx, -, sizeof(cx));
     memset(cy, -, sizeof(cy));
     for(int i = ; i <= tot; i++)
     {
         if(cx[i] == -)
         {
             memset(vis, , sizeof(vis));
             ans += dfs(i);
         }
     }
     return ans;
 }

 int main()
 {
     cin >> T;
     while(T--)
     {
         scanf("%d%d", &n, &m);
         tot = ;
         for(int i = ; i < maxn; i++)G[i].clear();
         for(int i = ; i < n; i++)//将Map转化成城市的编号
         {
             cin >> Map[i];
             for(int j = ; j < m ;j++)
                 if(Map[i][j] == 'o')cnt[i][j] = ;
                 else cnt[i][j] = ++tot;
         }/*
         for(int i = 0; i < n; i++)
         {
             for(int j = 0; j < m; j++)cout<<cnt[i][j]<<" ";
             cout<<endl;
         }*/
         for(int i = ; i < n; i++)
         //二分图建图，每个点拆成两个点，建成有向图，并且每两点之间有两条相反边，所以求出来的最大匹配是真正匹配的两倍
         {
             for(int j = ; j < m; j++)
             {
                 if(!cnt[i][j])continue;
                 for(int k = ; k < ; k++)
                 {
                     int xx = i + dir[k][];
                     int yy = j + dir[k][];
                     if(!cnt[xx][yy])continue;
                     if(xx <  || xx >= n || yy <  || yy >= m)continue;
                     int u = cnt[i][j], v = cnt[xx][yy];
                     //cout<<u<<" "<<v<<endl;
                     G[u].push_back(v);
                 }
             }
         }
         //最小路径覆盖数 = 顶点数 - 最大匹配数
         int ans = tot - maxmatch() / ;
         cout<<ans<<endl;
     }
     return ;
 }