【CCPC-Wannafly Winter Camp Day4 (Div1) D】欧拉回路（分类讨论）

点此看题面

大致题意： 有一个\(n\)行\(m\)列的网格图，让你给每一条边设置一个通过次数（\(\ge1\)），使其成为欧拉回路，且通过次数总和最小。

初始化

首先，由于通过次数\(\ge1\)，因此首先必然设置每条边通过次数为\(1\)。

对于一个\(n\)行\(m\)列的网格图，共有\(n(m-1)+m(n-1)\)条边，如下图：

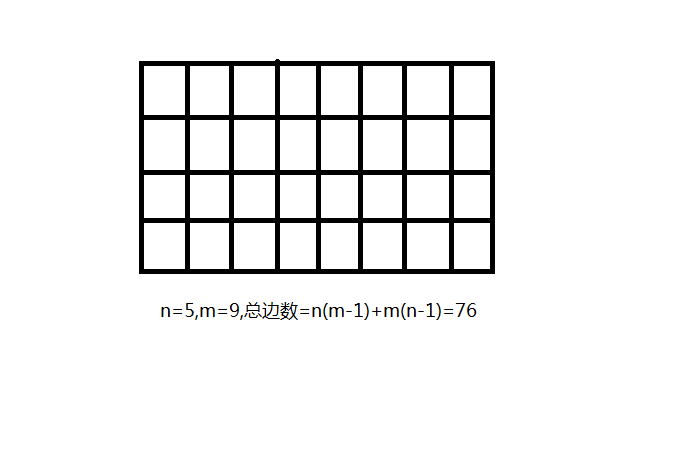
所以，初始化\(ans\)为\(n(m-1)+m(n-1)\)。

仔细观察上图，可以发现，中间的点以及四个角落的点都为偶点，因此只需给边上的点连边，使其全为偶点即可。

但又需要分类讨论。

当\(n,m\)都为偶数时

如图所示：

考虑将两条邻边作为一组。

则我们可以将同一组中两条边的交点向旁边两点连边，这样交点仍为偶点，而交点旁边这两个点也变成了偶点。

这样每条边上剩下的奇点个数就为偶数了。

则我们依然对相邻的两点之间连一条边，这样就可以使所有点都变成偶点了。

加的边数为：

\[2(\frac{n-2}2+\frac{m-2}2)=n+m-4
\]

当\(n,m\)都为奇数时

如图所示：

考虑将两条邻边作为一组。

则我们可以将同一组中两条边的交点向旁边两点连边，这样交点仍为偶点，而交点旁边这两个点也变成了偶点。

这样每条边上剩下的奇点个数就为偶数了。

则我们依然对相邻的两点之间连一条边，这样就可以使所有点都变成偶点了。

加的边数为：

\[2(\frac{n-3}2+\frac{m-3}2)+4=n+m-2
\]

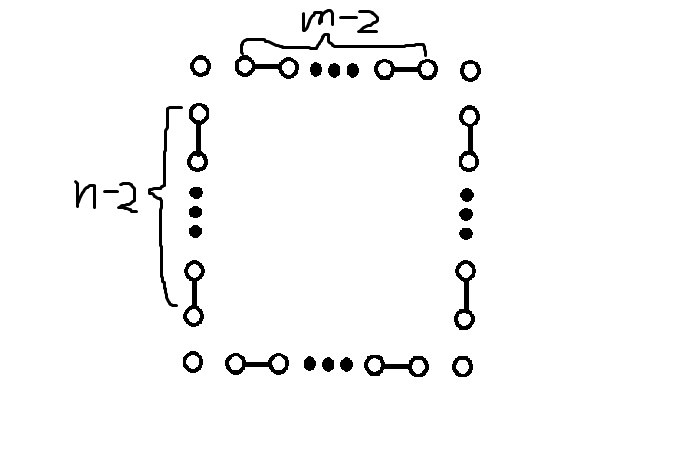
当\(n,m\)一奇一偶时

如图所示（假设\(n\)为奇数，\(m\)为偶数）：

我们把两条奇数边靠同一边的一个点一起向角上的点连边，然后剩下的\(n-3\)个点在相邻的两点之间连一条边。

其中被连过边的角上两点变成奇点，因此需向这条偶数边上两侧的点连一条边。此时这条边上剩下的\(m-4\)个点再在相邻的两点之间连一条边。

然后可以发现还有一条边上始终没有连过边，则直接在相邻的两点之间连一条边即可。

加的边数为：

\[2*\frac{n-3}2+\frac{m-4}2+\frac{m-2}2+4=n+m-2
\]

不难发现\(m\)为奇数，\(n\)为偶数时同理。

当\(n=2\)或\(m=2\)时

上面的分类讨论看似包含了所有情况，实则还有一种特殊情况没有考虑，即\(n=2\)或\(m=2\)时。

如图所示：

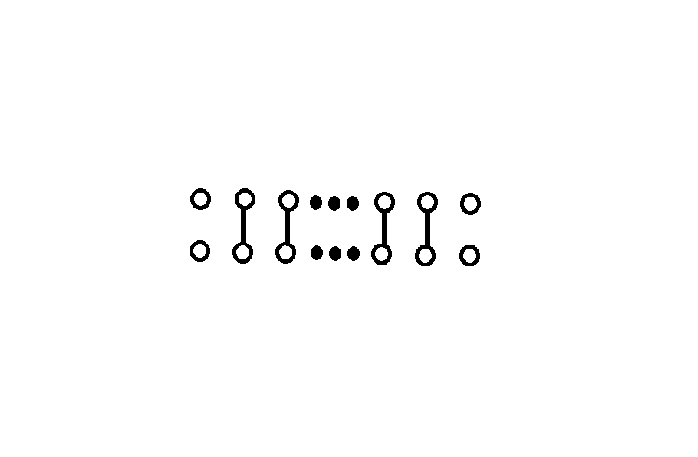
不难发现，\(n\)或\(m\)若有一个为\(2\)，则另一边的点可以与对边上的点两两相连。

加的边数为：

\[n-2\ or\ m-2
\]

总结

因此，对于给定的\(n\)和\(m\)，先初始化\(ans\)为\(n(m-1)+m(n-1)\)。

接下来，特判\(n=2\)或\(m=2\)的情况。

然后分奇偶性讨论，从上面的分析可以发现，在有至少一个奇数时加边数为\(n+m-2\)，若皆为偶数则加边数可以减\(2\)。

具体实现见代码。

代码

#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
using namespace std;
int n,m;
int main()
{
	scanf("%d%d",&n,&m);RI ans=n*(m-1)+m*(n-1);//读入+初始化ans
	if(n==2) return printf("%d",ans+m-2),0;if(m==2) return printf("%d",ans+n-2),0;//特判n=2或m=2的情况
	return ans+=n+m-2,!(n&1)&&!(m&1)&&(ans-=2),printf("%d",ans),0;//考虑一般情况，分奇偶性讨论
}