机器学习：多项式回归（scikit-learn中的多项式回归和 Pipeline）

一、scikit-learn 中的多项式回归

　1）实例过程

• 模拟数据

  import numpy as np
  import matplotlib.pyplot as plt
  
  x = np.random.uniform(-3, 3, size=100)
  X = x.reshape(-1, 1)
  y = 0.5 * x**2 + x + np.random.normal(0, 1, 100)

1. 相对于scikit-learn中的多项式回归，自己使用多项式回归，就是在使用线性回归前，改造了样本的特征；
2. sklearn 中，多项式回归算法（PolynomialFeatures）封装在了 preprocessing 包中，也就是对数据的预处理；
3. 对于多项式回归来说，主要做的事也是对数据的预处理，为数据添加一些新的特征；

• 使用 PolynomialFeatures 生成新的数据集

  from sklearn.preprocessing import PolynomialFeatures
  
  poly = PolynomialFeatures(degree=2)
  poly.fit(X)
  X2 = poly.transform(X)
  
  X2.shape
  # 输出：(100, 3)
  
  X2[:5, :]
  # 输出：
  array([[1.        , 2.98957009, 8.93752931],
         [1.        , 0.5481444 , 0.30046228],
         [1.        , 2.43260405, 5.91756246],
         [1.        , 1.86837318, 3.49081835],
         [1.        , 2.89120321, 8.35905598]])

1. degree=2：表示对原本数据集 X 添加一个最多为 2 次幂的相应的多项式特征；
2. poly.transform(X)：将原本数据集 X 的每一种特征，转化为对应的多项式的特征；
3. X2：生成的多项式特征相应的数据集；
4. 疑问：X 的样本原有一个特征，经过 PolynomialFeatures 后生成了 3 个特征？
5. X2 == [1., x, x²]；

• 使用 LinearRegression 类操作新的数据集 X2

  from sklearn.linear_model import LinearRegression
  
  lin_reg2 = LinearRegression()
  lin_reg2.fit(X2, y)
  y_predict2 = lin_reg2.predict(X2)

• 绘制拟合结果

  plt.scatter(x, y)
  plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
  plt.show()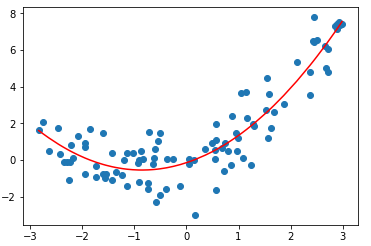

  

二、Pipeline（管道）

　1）疑问：如果数据集有 n 个特征，经过 PolynomialFeatures 生成的数据集有多少个？

• 模拟数据集

  X = np.arange(1, 11).reshape(-1, 2)
  X.shape
  # 输出：(5, 2)
  
  X
  # 输出：
  array([[ 1,  2],
         [ 3,  4],
         [ 5,  6],
         [ 7,  8],
         [ 9, 10]])

1. 当 degree = 2

   poly = PolynomialFeatures(degree=2)
   poly.fit(X)
   X2 = poly.transform(X)
   
   X2.shape
   # 输出：(5, 6)
   
   X2
   # 输出：
   array([[  1.,   1.,   2.,   1.,   2.,   4.],
          [  1.,   3.,   4.,   9.,  12.,  16.],
          [  1.,   5.,   6.,  25.,  30.,  36.],
          [  1.,   7.,   8.,  49.,  56.,  64.],
          [  1.,   9.,  10.,  81.,  90., 100.]])

2. 当 degree = 3

   poly = PolynomialFeatures(degree=3)
   poly.fit(X)
   X3 = poly.transform(X)
   
   X3.shape
   # 输出：(5, 10)
   
   X3
   # 输出：
   array([[   1.,    1.,    2.,    1.,    2.,    4.,    1.,    2.,    4.,    8.],
          [   1.,    3.,    4.,    9.,   12.,   16.,   27.,   36.,   48.,   64.],
          [   1.,    5.,    6.,   25.,   30.,   36.,  125.,  150.,  180.,  216.],
          [   1.,    7.,    8.,   49.,   56.,   64.,  343.,  392.,  448.,  512.],
          [   1.,    9.,   10.,   81.,   90.,  100.,  729.,  810.,  900., 1000.]])

• 分析：经过 PolynomialFeatures 之后，样本特征呈指数增长，新增的特征包含了所有可能的所样式；

　2）Pipeline 过程

• 使用多项式回归的过程

1. 将原始数据集 X 讲过 PolynomialFeatures 算法，生成多项式的特征的样本的数据集；
2. 数据归一化（StandardScaler）：如果 degree 非常的大，样本生成的特征的数据的差距也会变动非常的大；
3. 将新的数据集传给线性回归算法：LinearRegression；

• Pipeline 将这 3 步合为一体，使得每次使用多项式回归时，不需要重复这 3 个过程；

• 具体操作过程

1. 模拟数据

   x = np.random.uniform(-3, 3, size=100)
   X = x.reshape(-1, 1)
   y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

2. 使用 Pipeline

   from sklearn.pipeline import Pipeline
   from sklearn.linear_model import LinearRegression
   from sklearn.preprocessing import PolynomialFeatures
   from sklearn.preprocessing import StandardScaler
   import numpy as np
   import matplotlib.pyplot as plt
   
   # 实例化 Pipeline
   poly_reg = Pipeline([
       ("poly", PolynomialFeatures(degree=2)),
       ("std_scaler", StandardScaler()),
       ("lin_reg", LinearRegression())
   ])
   
   poly_reg.fit(X, y)
   y_predict = poly_reg.predict(X)

3. 绘制拟合的结果

   plt.scatter(x, y)
   plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
   plt.show()