【bzoj3209】: 花神的数论题 数论-DP

【bzoj3209】: 花神的数论题

首先二进制数中1的个数最多就是64个

设所有<=n的数里二进制中1的个数为i的有a[i]个

那么答案就是

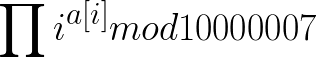 然后快速幂

求a[i]可以用DP

设在二进制中从高到低考虑到第k位，第k位之前的1的个数是cnt，n总共有len位

若第k位==1 那么 a[cnt+j]+=C(len-k,j) (j<=len-k)

其实就是前k-1位都与n前k-1位相等，第k位为0，后len-k随意选择j个1时对a的贡献

 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 #define ll long long
 const ll p=;
 ll n,len;
 ll c[][],a[];

 ll Q_pow(ll x,ll y){
     ll ans=;
     while (y){
         if (y&) ans=ans*x%p;
         x=x*x%p;
         y=(y>>);
     }
     return ans;
 }

 int main(){
     scanf("%lld",&n);
     for (ll x=n;x;x=(x>>)) len++;
     for (int i=;i<len;i++){
         c[i][]=c[i][i]=;
         for (int j=;j<i;j++){
             c[i][j]=c[i-][j]+c[i-][j-];
         }
     }
     int cnt=,ans=;
     for (int i=len-;i>=;i--){
         if (((n>>i)&)){
             for (int j=;j<=i;j++){
                 a[j+cnt]+=c[i][j];
             }
             cnt++;
         }
     }
     a[cnt]++;
     for (int i=;i<=len;i++){
         ans=ans*Q_pow(i,a[i])%p;
     }
     printf("%lld\n",ans);
     return ;
 }

感觉写的自己都看不懂