神经网络(BP)算法Python实现及简单应用

首先用Python实现简单地神经网络算法：

import numpy as np

# 定义tanh函数
def tanh(x):
    return np.tanh(x)

# tanh函数的导数
def tan_deriv(x):
    return 1.0 - np.tanh(x) * np.tan(x)

# sigmoid函数
def logistic(x):
    return 1 / (1 + np.exp(-x))

# sigmoid函数的导数
def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))

class NeuralNetwork:
    def __init__(self, layers, activation='tanh'):
        """
        神经网络算法构造函数
        :param layers: 神经元层数
        :param activation: 使用的函数（默认tanh函数）
        :return:none
        """
        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tan_deriv

        # 权重列表
        self.weights = []
        # 初始化权重（随机）
        for i in range(1, len(layers) - 1):
            self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25)
            self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25)

    def fit(self, X, y, learning_rate=0.2, epochs=10000):
        """
        训练神经网络
        :param X: 数据集（通常是二维）
        :param y: 分类标记
        :param learning_rate: 学习率（默认0.2）
        :param epochs: 训练次数（最大循环次数，默认10000）
        :return: none
        """
        # 确保数据集是二维的
        X = np.atleast_2d(X)

        temp = np.ones([X.shape[0], X.shape[1] + 1])
        temp[:, 0: -1] = X
        X = temp
        y = np.array(y)

        for k in range(epochs):
            # 随机抽取X的一行
            i = np.random.randint(X.shape[0])
            # 用随机抽取的这一组数据对神经网络更新
            a = [X[i]]
            # 正向更新
            for l in range(len(self.weights)):
                a.append(self.activation(np.dot(a[l], self.weights[l])))
            error = y[i] - a[-1]
            deltas = [error * self.activation_deriv(a[-1])]

            # 反向更新
            for l in range(len(a) - 2, 0, -1):
                deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]))
                deltas.reverse()
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a

使用自己定义的神经网络算法实现一些简单的功能：

小案例：

X:                  Y

0 0                 0

0 1                 1

1 0                 1

1 1                 0

 

from NN.NeuralNetwork import NeuralNetwork
import numpy as np

nn = NeuralNetwork([2, 2, 1], 'tanh')
temp = [[0, 0], [0, 1], [1, 0], [1, 1]]
X = np.array(temp)
y = np.array([0, 1, 1, 0])
nn.fit(X, y)
for i in temp:
    print(i, nn.predict(i))

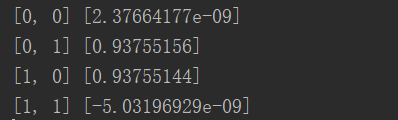
发现结果基本机制，无限接近0或者无限接近1

第二个例子：识别图片中的数字

导入数据：

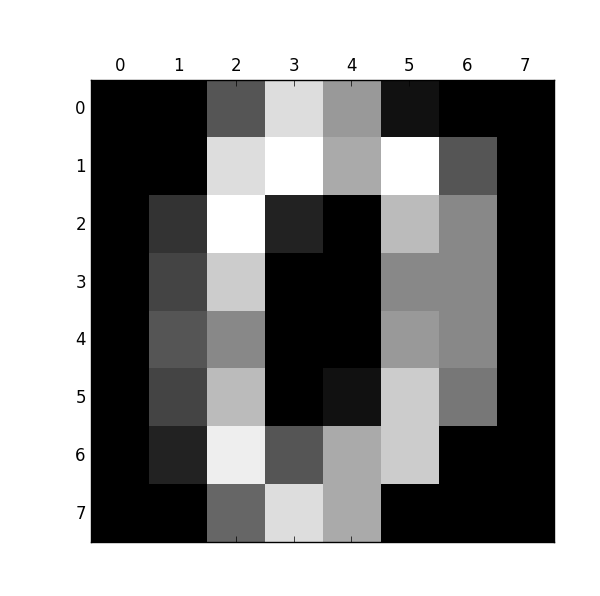
from sklearn.datasets import load_digits
import pylab as pl

digits = load_digits()
print(digits.data.shape)
pl.gray()
pl.matshow(digits.images[0])
pl.show()

观察下：大小：(1797, 64)

数字0

接下来的代码是识别它们：

import numpy as np
from sklearn.datasets import load_digits
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.preprocessing import LabelBinarizer
from NN.NeuralNetwork import NeuralNetwork
from sklearn.cross_validation import train_test_split

# 加载数据集
digits = load_digits()
X = digits.data
y = digits.target
# 处理数据，使得数据处于0,1之间，满足神经网络算法的要求
X -= X.min()
X /= X.max()

# 层数：
# 输出层10个数字
# 输入层64因为图片是8*8的，64像素
# 隐藏层假设100
nn = NeuralNetwork([64, 100, 10], 'logistic')
# 分隔训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)

# 转化成sklearn需要的二维数据类型
labels_train = LabelBinarizer().fit_transform(y_train)
labels_test = LabelBinarizer().fit_transform(y_test)
print("start fitting")
# 训练3000次
nn.fit(X_train, labels_train, epochs=3000)
predictions = []
for i in range(X_test.shape[0]):
    o = nn.predict(X_test[i])
    # np.argmax:第几个数对应最大概率值
    predictions.append(np.argmax(o))

# 打印预测相关信息
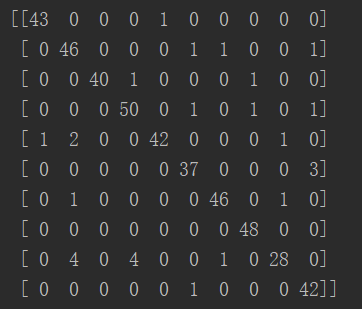
print(confusion_matrix(y_test, predictions))
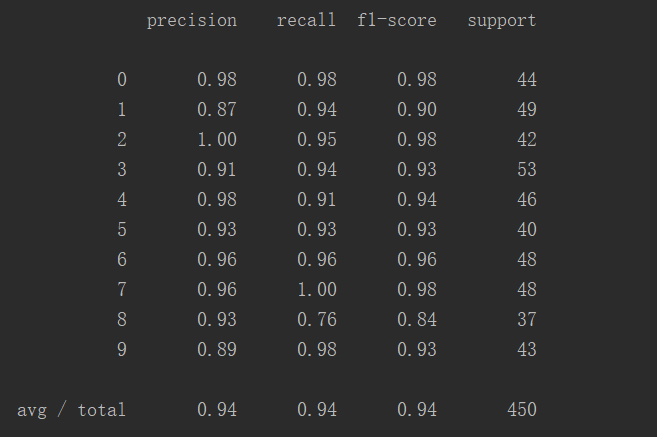
print(classification_report(y_test, predictions))

结果：

矩阵对角线代表预测正确的数量，发现正确率很多

这张表更直观地显示出预测正确率：

共450个案例，成功率94%