摘要

　　本文主要列举并求解了2016 ACM/ICPC亚洲区青岛站现场赛的部分真题，着重介绍了各个题目的解题思路，结合详细的AC代码，意在熟悉青岛赛区的出题策略，以备战2018青岛站现场赛。

HDU 5984 Pocky

题意

　　给出一根棒子（可以吃的）的长度x和切割过程中不能小于的长度d，每次随机的选取一个位置切开，吃掉左边的一半，对右边的棒子同样操作，直至剩余的长度不大于d时停止。现在给出x和d，问切割次数的数学期望是多少。

解题思路

　　当看到第二个样例2 1时，结果是1.693147，联想到ln(2) = 0.693147，可猜测当x > d时，答案是ln(x/d) + 1。

详细解法：

　　设长度为x、限制长度是d的棒切割次数的数学期望是f(x)，首先当x < d时，f(x) = 0（直接结束，切割次数为0）；当x >= d时，f(x) 应该是任选一点后，右边部分切割次数的数学期望加上1。设t是切割的位置，即，其中后面的式子表示切割点t的数学期望（积分0到x，取到这一点的概率乘上t的概率密度,也就是长度为t的切割次数的数学期望），进而又可以写成（积分中，系数可以自由进出），也即将f(x)写成如下形式

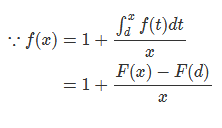
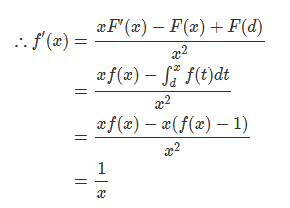
　　由此可得f(x) = ln(x) + c，当x = d时，f(d) = ln(d) + c = 1得，c = 1 - ln(d)，代入f(x) = ln(x) - ln(d) + 1，也即f(x) = ln(x/d) + 1;

综上所述

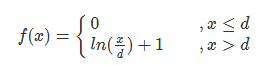
代码如下：

　　其中涉及C语言中对数的表示方法，C中只定义两log(double x)和log10(double x)，分别表示数学中的ln和lg，至于如何表示loga(b)呢？使用换底公式log(b)/log(a)即可。

  1.  #include <cstdio>
  2.  #include <cmath>
  3.  
  4.  int main()
  5.  {
  6.      double x, d;
  7.      int T;
  8.      scanf("%d", &T);
  9.      while(T--) {
  10.          scanf("%lf%lf", &x, &d);
  11.          if(x <= d)
  12.              printf("0.000000\n");
  13.          else
  14.              printf("%.6lf\n", log(x) - log(d) + );
  15.      }
  16.      return ;
  17.  }

HDU 5983 Pocket Cube

题意

　　输入一个二阶魔方的状态，问能否一步将其复原。

解题思路

　　需要细心和耐心，考虑每一种拧法，操作的时候，先顺时针改变一个面的数，然后改变四周的数，写出操作模板。要特别注意输入状态的次序，哪个面先，以及哪个角先。

代码如下：

  1.  #include <cstdio>
  2.  
  3.  struct Magic2{
  4.      int f[], b[], u[], d[], l[], r[];
  5.      void get_u() {for(int i =  ; i <= ; i++) {scanf("%d", &u[i]);}}
  6.      void get_d() {for(int i =  ; i <= ; i++) {scanf("%d", &d[i]);}}
  7.      void get_f() {for(int i =  ; i <= ; i++) {scanf("%d", &f[i]);}}
  8.      void get_b() {for(int i =  ; i <= ; i++) {scanf("%d", &b[i]);}}
  9.      void get_l() {for(int i =  ; i <= ; i++) {scanf("%d", &l[i]);}}
  10.      void get_r() {for(int i =  ; i <= ; i++) {scanf("%d", &r[i]);}}
  11.      void L(int cnt) {
  12.          for(; cnt > ; cnt--) {
  13.              int a[];
  14.              for(int i = ; i <= ; i++) a[i] = l[i];
  15.              l[] = a[];l[] = a[];
  16.              l[] = a[];l[] = a[];
  17.  
  18.              int x = b[], y = b[];
  19.              b[] = d[], b[] = d[];
  20.              d[] = f[], d[] = f[];
  21.              f[] = u[], f[] = u[];
  22.              u[] = x, u[] = y;
  23.          }
  24.      }
  25.      void R(int cnt) {
  26.          for(; cnt > ; cnt--) {
  27.              int a[];
  28.              for(int i = ; i <= ; i++) a[i] = r[i];
  29.              r[] = a[], r[] = a[];
  30.              r[] = a[], r[] = a[];
  31.  
  32.              int x = b[], y = b[];
  33.              b[] = u[], b[] = u[];
  34.              u[] = f[], u[] = f[];
  35.              f[] = d[], f[] = d[];
  36.              d[] = x, d[] = y;
  37.          }
  38.      }
  39.      void U(int cnt) {
  40.              for(; cnt > ; cnt--) {
  41.              int a[];
  42.              for(int i = ; i <= ; i++) a[i] = u[i];
  43.              u[] = a[], u[] = a[];
  44.              u[] = a[], u[] = a[];
  45.  
  46.              int x = b[], y = b[];
  47.              b[] = l[], b[] = l[];
  48.              l[] = f[], l[] = f[];
  49.              f[] = r[], f[] = r[];
  50.              r[] = x, r[] = y;
  51.          }
  52.      }
  53.      void D(int cnt) {
  54.          for(; cnt > ; cnt--) {
  55.              int a[];
  56.              for(int i = ; i <= ; i++) a[i] = d[i];
  57.              d[] = a[], d[] = a[];
  58.              d[] = a[], d[] = a[];
  59.  
  60.              int x = b[], y = b[];
  61.              b[] = r[], b[] = r[];
  62.              r[] = f[], r[] = f[];
  63.              f[] = l[], f[] = l[];
  64.              l[] = x, l[] = y;
  65.          }
  66.      }
  67.      void F(int cnt) {
  68.          for(; cnt > ; cnt--) {
  69.              int a[];
  70.              for(int i = ; i <= ; i++) a[i] = f[i];
  71.              f[] = a[], f[] = a[];
  72.              f[] = a[], f[] = a[];
  73.  
  74.              int x = u[], y = u[];
  75.              u[] = l[], u[] = l[];
  76.              l[] = d[], l[] = d[];
  77.              d[] = r[], d[] = r[];
  78.              r[] = x, r[] = y;
  79.          }
  80.      }
  81.      void B(int cnt) {
  82.          for(; cnt > ; cnt--) {
  83.              int a[];
  84.              for(int i = ; i <= ; i++) a[i] = u[i];
  85.              u[] = a[], u[] = a[];
  86.              u[] = a[], u[] = a[];
  87.  
  88.              int x = u[], y = u[];
  89.              u[] = r[], u[] = r[];
  90.              r[] = d[], r[] = d[];
  91.              d[] = l[], d[] = l[];
  92.              l[] = x, l[] = y;
  93.          }
  94.      }
  95.      bool ok() {
  96.          for(int i = ; i <= ; i++) {
  97.              if(u[i] != u[] || d[i] != d[]
  98.              || l[i] != l[] || r[i] != r[]
  99.              || f[i] != f[] || b[i] != b[])
  100.                  return ;
  101.          }
  102.          return ;
  103.      }
  104.      bool operate(char ch) {
  105.          if(ch == 'u') {
  106.              U();
  107.              if(ok())
  108.                  return ;
  109.              else {
  110.                  U();
  111.                  U();
  112.                  if(ok())
  113.                      return ;
  114.                  else{
  115.                      U();
  116.                      return ;
  117.                  }
  118.              }
  119.          }
  120.          if(ch == 'd') {
  121.              D();
  122.              if(ok())
  123.                  return ;
  124.              else{
  125.                  D();
  126.                  D();
  127.                  if(ok())
  128.                      return ;
  129.                  else{
  130.                      D();
  131.                      return ;
  132.                  }
  133.              }
  134.          }
  135.          if(ch == 'f') {
  136.              F();
  137.              if(ok())
  138.                  return ;
  139.              else{
  140.                  F();
  141.                  F();
  142.                  if(ok())
  143.                      return ;
  144.                  else{
  145.                      F();
  146.                      return ;
  147.                  }
  148.              }
  149.          }
  150.          if(ch == 'b') {
  151.              B();
  152.              if(ok())
  153.                  return ;
  154.              else{
  155.                  B();
  156.                  B();
  157.                  if(ok())
  158.                      return ;
  159.                  else{
  160.                      B();
  161.                      return ;
  162.                  }
  163.              }
  164.          }
  165.          if(ch == 'l') {
  166.              L();
  167.              if(ok())
  168.                  return ;
  169.              else{
  170.                  L();
  171.                  L();
  172.                  if(ok())
  173.                      return ;
  174.                  else{
  175.                      L();
  176.                      return ;
  177.                  }
  178.              }
  179.          }
  180.          if(ch == 'r') {
  181.              R();
  182.              if(ok())
  183.                  return ;
  184.              else{
  185.                  R();
  186.                  R();
  187.                  if(ok())
  188.                      return ;
  189.                  else{
  190.                      R();
  191.                      return ;
  192.                  }
  193.              }
  194.          }
  195.      }
  196.      void print() {
  197.          puts("###");
  198.          for(int i = ; i <= ; i++) printf("%d ", u[i]); puts("");
  199.          for(int i = ; i <= ; i++) printf("%d ", f[i]); puts("");
  200.          for(int i = ; i <= ; i++) printf("%d ", d[i]); puts("");
  201.          for(int i = ; i <= ; i++) printf("%d ", b[i]); puts("");
  202.          for(int i = ; i <= ; i++) printf("%d ", l[i]); puts("");
  203.          for(int i = ; i <= ; i++) printf("%d ", r[i]); puts("");
  204.      }
  205.  }m2;
  206.  
  207.  int main()
  208.  {
  209.      int T;
  210.      scanf("%d", &T);
  211.      while(T--) {
  212.          m2.get_u();
  213.          m2.get_f();
  214.          m2.get_d();
  215.          m2.get_b();
  216.          m2.get_l();
  217.          m2.get_r();
  218.          if(m2.ok() || m2.operate('u') || m2.operate('d') || m2.operate('l')
  219.          || m2.operate('r') || m2.operate('f') || m2.operate('b'))
  220.              printf("YES\n");
  221.          else
  222.              printf("NO\n");
  223.      }
  224.      return ;
  225.  }

HDU 5985 Lucky Coins

题意

　　给出n个硬币和每个硬币的数量和正面朝上的概率，问每个硬币成为幸运硬币的概率是多少。成为幸运硬币的条件是每投一次将所有背面朝上的硬币去掉，继续抛掷，直至剩下一种或者一个都剩下，那最后一种留下的硬币就是幸运硬币。

解题思路

　　概率DP，我们定义dead[i][j]表示第i种硬币在前j步以内全部被抛弃的概率，显然，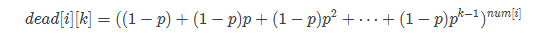

化简可得 .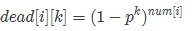

　　那么我们定义aliv[i][j] 表示第i种硬币在前j步以内至少有一个没有被抛弃的概率是 1 - dead[i][j]，那么第i个硬币成为幸运硬币的概率大概等于（应为当k = 30的时候0.5的三十次方就很小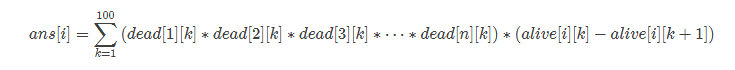），其实际意义就是第i种硬币成为幸运硬币的概率等于模拟投掷100次，而每次让第1到n种硬币在k步全部被抛弃的概率乘上第i种硬币在第k步至少还有一个而第k+1步全部被抛弃的概率，当然前面的第1到第n种硬币全部被抛弃不包括第i种硬币，故完整的式子是：

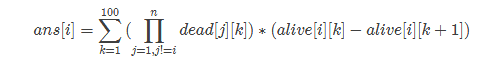
代码如下:

  1.  #include <iostream>
  2.  #include <cstdio>
  3.  #include <cmath>
  4.  #include <cstring>
  5.  
  6.  using namespace std;
  7.  
  8.  const int maxn = ;
  9.  int n;
  10.  double num[maxn], p[maxn], ans[maxn];
  11.  double dead[maxn][], alive[maxn][];
  12.  
  13.  void cdead() {
  14.      for(int k = ; k <= ; k++) {
  15.          for(int i = ; i < n; i++) {
  16.              dead[i][k] = pow(1.0 - pow(p[i], k), num[i]);
  17.          }
  18.      }
  19.  }
  20.  void calive() {
  21.      for(int k = ; k <= ; k++) {
  22.          for(int i = ; i < n; i++) {
  23.              alive[i][k] = 1.0 - dead[i][k];
  24.          }
  25.      }
  26.  }
  27.  
  28.  int main()
  29.  {
  30.      int T;
  31.      scanf("%d", &T);
  32.      while(T--) {
  33.          scanf("%d", &n);
  34.          for(int i = ; i < n; i++) {
  35.              scanf("%lf%lf", &num[i], &p[i]);
  36.          }
  37.          if(n == ) {
  38.              printf("1.000000\n");
  39.              continue;
  40.          }
  41.  
  42.          cdead();
  43.          calive();
  44.          memset(ans, , sizeof(ans));
  45.          for(int k = ; k <= ; k++) {
  46.              for(int i = ; i < n; i++) {
  47.                  double tmp = ;
  48.                  for(int j = ; j < n; j++) {
  49.                      if(j == i)  continue;
  50.                      tmp *= dead[j][k];
  51.                  }
  52.                  ans[i] += tmp * (alive[i][k] - alive[i][k + ]);
  53.              }
  54.          }
  55.  
  56.          for(int i = ; i < n; i++) {
  57.              printf("%.6lf%c", ans[i], i == n -  ? '\n' : ' ');
  58.          }
  59.      }
  60.      return ;
  61.  }

　　可以看出青岛站的题目还是有难度的，主要侧重的是数学推理，准备时应该多以数学推理为主，大战在即，加油！

2016 ACM/ICPC亚洲区青岛站现场赛（部分题解）的更多相关文章

  1. 2016 ACM/ICPC亚洲区大连站-重现赛 解题报告

    任意门:http://acm.hdu.edu.cn/showproblem.php?pid=5979 按AC顺序: I - Convex Time limit    1000 ms Memory li ...

  2. 2016 ACM/ICPC亚洲区青岛站

    A B C D E F G H I J K L M O O O O     $\varnothing$     $\varnothing$  $\varnothing$  $\varnothing$  ...

  3. 2013ACM/ICPC亚洲区南京站现场赛---Poor Warehouse Keeper(贪心)

    题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=4803 Problem Description Jenny is a warehouse keeper. ...

  4. 2016ACM/ICPC亚洲区大连站现场赛题解报告（转）

    http://blog.csdn.net/queuelovestack/article/details/53055418 下午重现了一下大连赛区的比赛,感觉有点神奇,重现时居然改了现场赛的数据范围,原 ...

  5. 2013ACM/ICPC亚洲区南京站现场赛——题目重现

    GPA http://acm.hdu.edu.cn/showproblem.php?pid=4802 签到题,输入两个表,注意细心点就行了. #include<cstdio> #inclu ...

  6. hdu4811-Ball(2013ACM/ICPC亚洲区南京站现场赛)

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4811 题目描述: Problem Description Jenny likes balls. He ...

  7. 2013ACM/ICPC亚洲区南京站现场赛-HDU4809(树形DP)

    为了这个题解第一次写东西..(我只是来膜拜爱看touhou的出题人的).. 首先以为对称性质..我们求出露琪诺的魔法值的期望就可以了..之后乘以3就是答案..(话说她那么笨..能算出来么..⑨⑨⑨⑨⑨ ...

  8. 2016 ACM/ICPC亚洲区大连站 F - Detachment 【维护前缀积、前缀和、二分搜索优化】

    F - Detachment In a highly developed alien society, the habitats are almost infinite dimensional spa ...

  9. 2014ACM/ICPC亚洲区西安站现场赛 F color（二项式反演）

    题意:小球排成一排,从m种颜色中选取k种颜色给n个球上色,要求相邻的球的颜色不同,求可行的方案数,答案模1e9+7.T组数据,1<= n, m <= 1e9, 1 <= k < ...

随机推荐

  1. recyclerview刷新

    https://blog.csdn.net/leejizhou/article/details/51179233 RecyclerView之更新UI数据的高级用法 https://www.cnblog ...

  2. 【翻译】从头开始写一个时间序列数据库-Writing a Time Series Database from Scratch

    本文来自: https://fabxc.org/tsdb/, 如翻译有误,请纠正. 我是从事监控工作的.特别是Prometheus, 一个包含自定义的时间序列库以及集成Kuberntes的监控系统. ...

  3. CSS3变换、过渡、动画效果

    为元素创建圆角 1.四个相同的圆角 -webkit-border-radius:10px; border-radius:10px; 2.一个圆角 -webkit-border-top-left-rad ...

  4. Django积木块七——视频

    视频 # 在网上搜索video.js然后下载相关的js和css文件,看文档正确使用视频模块,添加视频外链 <div style="width: 1200px;height: 675px ...

  5. socket的阻塞与非阻塞，同步与非同步

    网络编程中通常提到四种方式,同步/异步,阻塞/非阻塞.以下对它们的概念进行总结 1.同步/异步:主要针对C端 同步:所谓同步,就是在C端发出一个功能调用时,在没有得到结果之前,调用不返回,也就是必须一 ...

  6. cordova 开发

    这个挺好用的, 确实 把一个 Android 和 IOS 的App 给生成了. html为前端, js调用 Java 或 object -C的代码. 加快了开发的进度 在不使用插件的基础上 ,基本实现 ...

  7. 【转】在Linux下安装python3

    原文链接:http://www.cnblogs.com/feng18/p/5854912.html 1.linux下安装python3 a. 准备编译环境(环境如果不对的话,可能遇到各种问题,比如wg ...

  8. 使用jquery实现文本框输入特效：文字逐个显示逐个消失反复循环

    前两天看到某个网站上的输入框有个小特效:文字逐个显示,并且到字符串最大长度后,逐个消失,然后重新循环显示消失,循环显示字符串数组.我对这个小特效有点好奇,于是今天自己尝试用jquery写一个简单的小d ...

  9. python爬虫学习之使用XPath解析开奖网站

    实例需求:运用python语言爬取http://kaijiang.zhcw.com/zhcw/html/ssq/list_1.html这个开奖网站所有的信息,并且保存为txt文件. 实例环境:pyth ...

  10. Java开发瓶颈，Dubbo架构学习整理

    作者:butterfly100 一. Dubbo诞生背景 随着互联网的发展和网站规模的扩大,系统架构也从单点的垂直结构往分布式服务架构演进,如下图所示: 单一应用架构:一个应用部署所有功能,此时简化C ...