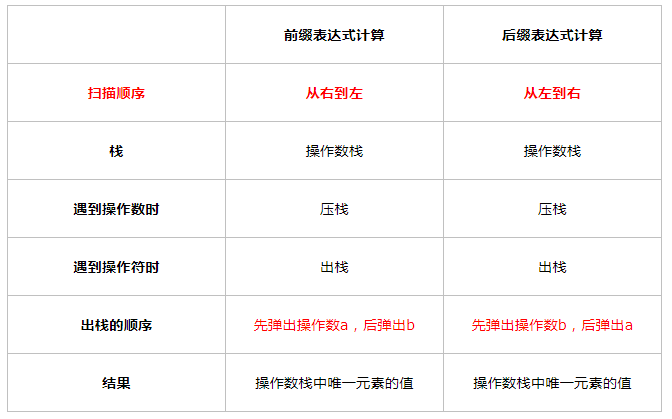
python-中缀表达式转前缀表达式

作完了中缀前缀，作一个归纳吧。

https://www.cnblogs.com/unixfy/p/3344550.html

# coding = utf-8

class Stack:
    def __init__(self):
        self.items = []

    # 是否为空
    def is_empty(self):
        return self.items == []

    # 进栈
    def push(self, item):
        self.items.append(item)

    # 出栈
    def pop(self):
        return self.items.pop()

    # 返回栈顶值，不改变栈
    def peek(self):
        return self.items[len(self.items) - 1]

    # 返回栈长度
    def size(self):
        return len(self.items)

def infix_to_prefix(infix_expr):
    prec = dict()
    prec[")"] = 4
    prec["*"] = 3
    prec["/"] = 3
    prec["+"] = 2
    prec["-"] = 2
    prec["("] = 1
    prefix_expr = []
    s = Stack()
    # 从右到左扫描
    for item in reversed(infix_expr.split()):
        # 如果标记是操作数，将其附加到输出列表的末尾
        if item not in prec.keys():
            prefix_expr.append(item)
        # 如果标记是右括号，将其压到 s 上
        elif item == ')':
            s.push(item)
        # 如果标记是左括号，则弹出 s，直到删除相应的右括号。将每个运算符附加到
        # 输出列表的末尾
        elif item == '(':
            while s.peek() != ')':
                prefix_expr.append(s.pop())
            s.pop()
        # 如果标记是运算符， *，/，+  或  -  ，将其压入 s。但是，首先删除已经在
        # s 中具有更高或相等优先级的任何运算符，并将它们加到输出列表中
        else:
            while (not s.is_empty())\
                    and s.peek() != ')'\
                    and prec[s.peek()] > prec[item]:
                prefix_expr.append(s.pop())
                s.push(item)
            s.push(item)
        print(s.items)
    # 当输入表达式被完全处理时，检查 s。仍然在栈上的任何运算符都可以删除并加到
    # 输出列表的末尾
    while not s.is_empty():
        prefix_expr.append(s.pop())
    # 反转序列
    prefix_expr.reverse()
    return ' '.join(prefix_expr)

def prefix_eval(prefix_expr):
    s = Stack()
    for item in reversed(prefix_expr.split()):
        # 如果不是运算符号，压栈
        if item not in '+-*/':
            s.push(item)
        else:　　　　　　　# 和后缀相反顺序　
            op1 = int(s.pop())
            op2 = int(s.pop())
            print(op1, item, op2)
            result = do_match(item, op1, op2)
            s.push(result)
        print(s.items)
    return result

# 运行结果
def do_match(op, op1, op2):
    if op == '+':
        return op1 + op2
    elif op == '-':
        return op1 - op2
    elif op == '*':
        return op1 * op2
    elif op == '/':
        return op1 / op2
    else:
        raise Exception('Error operation!')

infix_str = '1 + ( ( 2 + 3 ) * 4 ) - 5'
prefix_output = infix_to_prefix(infix_str)
print(infix_str)
print(prefix_output)
prefix_result = prefix_eval(prefix_output)
print(prefix_result)

　　

输出：

C:\Users\Sahara\.virtualenvs\untitled\Scripts\python.exe D:/test/python_stack.py
[]
['-']
['-', ')']
['-', ')']
['-', ')', '*']
['-', ')', '*', ')']
['-', ')', '*', ')']
['-', ')', '*', ')', '+']
['-', ')', '*', ')', '+']
['-', ')', '*']
['-']
['-', '+']
['-', '+']
1 + ( ( 2 + 3 ) * 4 ) - 5
- + 1 * + 2 3 4 5
['5']
['5', '4']
['5', '4', '3']
['5', '4', '3', '2']
2 + 3
['5', '4', 5]
5 * 4
['5', 20]
['5', 20, '1']
1 + 20
['5', 21]
21 - 5
[16]
16

Process finished with exit code 0