简单的量子算法(一)：Hadamard 变换、Parity Problem

Hadamard Transform

Hadamard 变换在量子逻辑门中提过，只不过那时是单量子的Hadamard门，负责把$|1\rangle$变成$|-\rangle$，$|0\rangle$变成$|+\rangle$。

那么对多量子的Hadamard门呢？

对于多量子逻辑门，其实说过一句，是单量子逻辑门的张量积。

对于多量子比特的Hadamard门，就是把每一个量子比特都由$|1\rangle$变成$|-\rangle$，$|0\rangle$变成$|+\rangle$，或者$|-\rangle$变成$|1\rangle$，$|+\rangle$变成$|0\rangle $ 。如果是n个比特，那么这n比特的Hadamard门就可以写作是 $H^{\otimes n}$ ，矩阵表达就是 $H^{\otimes n}=\left[ \begin{array}{}{\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{array}\right] \otimes ……\otimes \left[ \begin{array}{}{\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{array}\right]$ （张量积n次）

对于$|0\rangle$，变成$\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle$。

对于$|00\rangle$，变成$(\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle)(\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle)$ ，即 $\frac{1}{2}|00\rangle+\frac{1}{2}|01\rangle+\frac{1}{2}|10\rangle+\frac{1}{2}|11\rangle$ 可能性均等的所有可能的叠加。

那么对于n个 $|0\rangle$ 呢？则是变成了 $\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle$ ，x是由0、1组成的所有的长度为n的数字串。

输出是：$\sum_x \frac{-1^{u·x}}{2^{\frac{n}{2}}} |x\rangle$ ,这里 $u·x=u_1x_1+u_2x_2+……+u_nx_n$

原因如下：

对于$|0\rangle$，H门变成$\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle$

对于$|1\rangle$，H门变成$\frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle$

如果想要有一个负号，则需要这一位在输入的时候是$|1\rangle$ ，并且输出的时候也是 $|1\rangle$ ，同时，如果在这个数字串中这种情况出现了偶数次（即有偶数位的比特在输入输出的时候都是$|1\rangle$），那么整体情况就会是负负得正，所以我们将每位的情况相乘，再连加（对于不会造成负号的情况，他们相乘的结果是0），作为-1的指数来标明符号。

而以上的变换，在量子计算中又称为Fourier Sampling。

整理一下本小节的内容： $H^{\otimes n} |u\rangle = \sum_x \frac{-1^{u·x}}{2^{\frac{n}{2}}} |x\rangle$ ，他将我们的输入数据给移到了符号上面去。

Parity Problem

这个问题是hadamard变换的简单应用。

假设： 有这么一个黑盒子把长度为n的0、1数字串映射成0或者1一个数字 $f: \{ 0,1 \}^n \rightarrow \{0,1 \}$ ，已知映射的规则如下 $f(x)=u·x=u_1x_1+u_2x_2+……+u_nx_n \mod 2$ 模2的意思是如果是累加的和是奇数，那么就是1，偶数就是0

问题：请问，我至少需要试几次，才能知道u是什么？

经典解法：

输入100……0 得到$u_1$ 的值

输入010……0 得到$u_2$ 的值

输入001……0 得到$u_3$ 的值

……

输入000……1 得到$u_n$ 的值

因为我们的输出结果只有一位的信息，而u的全部信息有n位，所以我们至少也需要n次。

量子解法：

这个量子解法又叫做 Bernstein-Vazirani算法，一共只有两步：

一、制造出一个量子叠加态： $\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle $

二、对这个叠加态fourier sampling

why?

对于第一步我们需要制备出来的量子叠加态，不知道大家有没有眼熟，这个是我们上一节的结论，将$|u\rangle$ 作为H门的输出得到的结果一模一样。

我们已经知道了量子计算是可逆的，对于H门来说，连续两个的H门操作就是完全抵消的，第一个H门将$|0\rangle$变成$|+\rangle$，第二个H门又将$|+\rangle$变成$|0\rangle$。

所以，我们能够将$\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle $用H门变换出来，把f(x)的值移到符号上，那么我们也可以通过H门把符号上的f(x)移到输出里，只需要一个同样的H门操作，也就是我们的第二步。

所以现在的问题变成了，如果制备叠加态 $\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle $ 呢？

在量子电路里面我们已经讨论过了，一个量子的电路，为了让他可逆，我们一般是输入 $|x\rangle|b\rangle$ 然后输出是 $|x\rangle |b \oplus f(x) \rangle$ 把输入的结果f(x)模2加到b上。

因为是需要所有的x，所以首先用H门，将n比特的 $|0\rangle$ 变成所有状态均可能的叠加态 $\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle$ 。

接下来，把 $|-\rangle =\frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle$ 作为 $|b\rangle$ 和前面的叠加态 $\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle$ 一起输入 $U_f$ 。

此时输入是 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle |-\rangle$

输出是 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle |- \oplus f(x) \rangle$

如果f(x)=0 那么$|- \oplus f(x) \rangle = \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle = |-\rangle$

如果f(x)=1 那么$|- \oplus f(x) \rangle = \frac{1}{\sqrt2}|1\rangle-\frac{1}{\sqrt2}|0\rangle = -|-\rangle$

最后一个比特的值如果在$|+\rangle |-\rangle$坐标下测量，一定是 $|-\rangle$，f(x)的差别也变到了符号上，即 $(-1)^{f(x)}$

此时，我们的输出已经是 $\frac{1}{2^{n/2}}\sum_x (-1)^{f(x)} |x\rangle |-\rangle$ ，只看前面的部分，就是我们需要的叠加态了。

概括一下，概括一下，通过H门制备出一个均等可能的态，然后和 $|-\rangle$ 一起通过 $U_f$ 将f(x)的结果移到符号上，最后再次通过H门，把符号上的结果移下来，整个电路图如下图所示，非常的简单，在经典算法需要多项式时间的时候，量子算法只需要常数的时间。

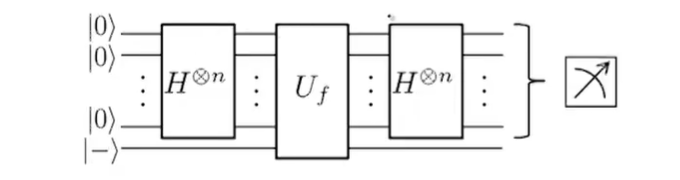
下一篇的内容是simon's Algorithm是在parity Problem的又一个进化，也是基于H门的，所以说H门很重要啊，基本上所有的量子算法不管要干嘛，先来一个H门再说，毕竟这个是用n比特同时表达 $2^n$ 个数据的法宝。

参考资料：
Quantume Mechanics & Quantume Computation Lecture 8