minimize.m:共轭梯度法更新BP算法权值

minimize.m:共轭梯度法更新BP算法权值

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

Carl Edward Rasmussen在高斯机器学习的MATLAB代码中写到一个优化类的函数：minimize.m，同时，Geoff Hinton在用BP算法精调深度自编码网络时，也借鉴了这个函数minimize.m，下面来简单聊一聊这个函数的大致机理。

matlab函数minimum.m用来查找（非线性）多元函数的（局部）最小值。用户必须提供一个函数，该函数返回所有变量的值和偏导数。该函数基于具有Wolfe-Powel条件的多项式插值，使用Polak-Ribiere共轭梯度和近似线性搜索。

作用：Minimize a differentiable multivariate function.

1. 线性搜索技术——确定迭代步长

2. 非线性共轭梯度法——确定搜索方向

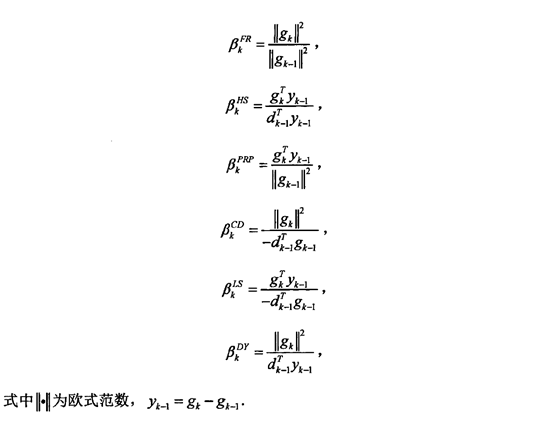
3. MATLAB代码详解

function [X, fX, i] = minimize(X, f, length, varargin)
%X是权值偏置 f输出的是代价函数和偏导 3次线性搜索 每层网络对应的节点数Dim和训练数据data
%f是一个函数的名称，它主要是用来计算网络中的代价函数以及代价函数对各个参数X的偏导函数，f的参数值分别为X，以及minimize函数后面的P1,P2,P3,…使用共轭梯度法进行优化的最大线性搜索长度为length。
%返回值X为3次线性搜索最优化后得到的权值参数，是一个列向量，fX为在此最优参数X下的代价函数，i为线性搜索的长度（即迭代的次数）。

% Minimize a differentiable multivariate function.
%
% Usage: [X, fX, i] = minimize(X, f, length, P1, P2, P3, ... )

%更新参数W和b，ΔW=步长*方向,Δb=步长*方向。步长用Wolfe不确定线性搜索进行计算，而下降的方向用Polack-Ribiere共轭梯度进行计算。最终输出更新完之后的参数W,b

%最小化连续微分多元函数。

%起点由“ X”（D乘1）给定，并且在字符串“ f”中命名的函数必须返回函数值和偏导数向量。
%共轭梯度的Polack-Ribiere风格用于计算搜索方向，并且使用二次多项式和三次多项式逼近以及Wolfe-Powell停止准则的线搜索以及斜率比方法来猜测初始步长。
%此外，还要进行大量检查，以确保正在进行探索，并且推断不会无边无际。
%“length”给出了运行的长度：如果为正，则给出最大的线性搜索次数；如果为负，则其绝对值给出最大的函数求值次数。
%当函数的长度变长或无法进一步进行处理时（即，我们处于最小状态，或由于数值问题而接近时，我们无法进一步接近），该函数将返回。
%如果函数在几次迭代中终止，则可能表明函数值和导数不一致（即，“ f”函数的实现中可能存在错误）。
%函数返回找到的解“ X”，函数值“ fX”的向量表示进展，“ i”使用的迭代次数（线性搜索或函数评估，取决于“length”的符号）。

%当函数的长度增加或无法进一步处理时（即，我们处于（局部）最小值，或由于数值问题而接近），函数将返回。
%注意：如果函数在几次迭代中终止，则可能表明函数值和导数不一致（即，“ f”函数的实现中可能存在错误）。
%函数返回找到的解“ X”，函数值“ fX”的向量表示进展，“ i”使用的迭代次数（行搜索或函数评估，取决于“长度”的符号）。

INT = 0.1;    % don't reevaluate within 0.1 of the limit of the current bracket不要在当前括号限制的0.1以内重新评估
EXT = 3.0;                  % extrapolate maximum 3 times the current step-size外推最大值为当前步长的3倍
MAX = 20;                         % max 20 function evaluations per line search每次线性搜索最多20个函数求值
RATIO = 10;                                       % maximum allowed slope ratio最大允许斜率
SIG = 0.1; RHO = SIG/2;
% SIG和RHO是控制Wolfe-Powell条件的常数。
% SIG是先前斜率和新斜率（搜索方向上的导数）之间允许的最大绝对比率，因此将SIG设置为低（正）值将强制线搜索中的更高精度。
% RHO是期望值的最小允许分数（从线性搜索中起始点的斜率开始）。
% 常数必须满足0 <RHO <SIG <1。调整SIG（取决于要优化的函数的性质）可能会加快最小化；使用rho可能不值得。

%在开始沿着最陡下降的方向进行初始行搜索之后，代码自然分为3部分。
%1）我们首先进入一个while循环，它使用点1（p1）和（p2）来计算外推（p3），直到我们外推足够远（wolfe-powell条件）。
%2）如有必要，我们进入第二个循环，其中p2、p3和p4选择包含（局部）最小值的子区间，并对其进行插值，找到一个可接受的点（wolfe-powell条件）。请注意，点始终保持顺序p0<=p1<=p2<p3<p4。
%3）使用共轭梯度（polack-ribiere-flavor）计算新的搜索方向，或者在前一线性搜索中出现问题时恢复到最陡。
%如果两个连续的线性搜索失败，或者当函数计算或线性搜索用完时，返回迄今为止的最佳值。
%在外推过程中，“f”函数可能会因错误或返回nan或inf而失败，minimize应该能很好地处理这个问题。
if max(size(length)) == 2
    red=length(2);
    length=length(1);
else %length=3
    red=1;
end
if length>0
    S='Linesearch';  %线性搜索
else
    S='Function evaluation';  %函数求值
end

i = 0;                                            % zero the run length counter 运行长度计数器清零
ls_failed = 0;                             % no previous line search has failed先前的线性搜索没有失败
[f0 df0] = feval(f, X, varargin{:});          % get function value and gradient
fX = f0;
i = i + (length<0);                                            % count epochs?!
s = -df0; d0 = -s'*s;           % initial search direction (steepest) and slope初始搜索方向(最陡，负梯度方向)和斜率
x3 = red/(1-d0);                                  % initial step is red/(|s|+1) 初始步长

while i < abs(length)                                      % while not finished
  i = i + (length>0);                                      % count iterations?!

  X0 = X; F0 = f0; dF0 = df0;                   % make a copy of current values
  if length>0, M = MAX; else M = min(MAX, -length-i); end
  %用p1、p2外推p3
  while 1                             % keep extrapolating as long as necessary
    x2 = 0; f2 = f0; d2 = d0; f3 = f0; df3 = df0;
    success = 0;
    while ~success && M > 0
      try
        M = M - 1; i = i + (length<0);                         % count epochs?!
        [f3 df3] = feval(f, X+x3*s, varargin{:});    %权值(t+1)=权值(t)+初始步长*初始搜索方向
        if isnan(f3) || isinf(f3) || any(isnan(df3)+isinf(df3)), error(''), end
        success = 1;
      catch                                % catch any error which occured in f
        x3 = (x2+x3)/2;                                  % bisect and try again  %步长等分，选取新搜索点
      end
    end
    if f3 < F0, X0 = X+x3*s; F0 = f3; dF0 = df3; end         % keep best values
    d3 = df3'*s;                                                    % new slope
    if d3 > SIG*d0 || f3 > f0+x3*RHO*d0 || M == 0  % are we done extrapolating?
      break
    end
    x1 = x2; f1 = f2; d1 = d2;                        % move point 2 to point 1
    x2 = x3; f2 = f3; d2 = d3;                        % move point 3 to point 2
    A = 6*(f1-f2)+3*(d2+d1)*(x2-x1);                 % make cubic extrapolation
    B = 3*(f2-f1)-(2*d1+d2)*(x2-x1);
    x3 = x1-d1*(x2-x1)^2/(B+sqrt(B*B-A*d1*(x2-x1))); % num. error possible, ok!
    if ~isreal(x3) || isnan(x3) || isinf(x3) || x3 < 0 % num prob | wrong sign?
      x3 = x2*EXT;                                 % extrapolate maximum amount
    elseif x3 > x2*EXT                  % new point beyond extrapolation limit?
      x3 = x2*EXT;                                 % extrapolate maximum amount
    elseif x3 < x2+INT*(x2-x1)         % new point too close to previous point?
      x3 = x2+INT*(x2-x1);
    end
  end                                                       % end extrapolation
  %插值p2、p3和p4
  while (abs(d3) > -SIG*d0 || f3 > f0+x3*RHO*d0) && M > 0  % keep interpolating
    if d3 > 0 || f3 > f0+x3*RHO*d0                         % choose subinterval
      x4 = x3; f4 = f3; d4 = d3;                      % move point 3 to point 4
    else
      x2 = x3; f2 = f3; d2 = d3;                      % move point 3 to point 2
    end
    if f4 > f0
      x3 = x2-(0.5*d2*(x4-x2)^2)/(f4-f2-d2*(x4-x2));  % quadratic interpolation 二次插值
    else
      A = 6*(f2-f4)/(x4-x2)+3*(d4+d2);                    % cubic interpolation 三次插值
      B = 3*(f4-f2)-(2*d2+d4)*(x4-x2);
      x3 = x2+(sqrt(B*B-A*d2*(x4-x2)^2)-B)/A;        % num. error possible, ok!
    end
    if isnan(x3) || isinf(x3)
      x3 = (x2+x4)/2;               % if we had a numerical problem then bisect
    end
    x3 = max(min(x3, x4-INT*(x4-x2)),x2+INT*(x4-x2));  % don't accept too close
    [f3 df3] = feval(f, X+x3*s, varargin{:});
    if f3 < F0, X0 = X+x3*s; F0 = f3; dF0 = df3; end         % keep best values
    M = M - 1; i = i + (length<0);                             % count epochs?!
    d3 = df3'*s;                                                    % new slope
  end                                                       % end interpolation
  %用Polack-Ribiere共轭梯度法更新搜索方向
  if abs(d3) < -SIG*d0 && f3 < f0+x3*RHO*d0          % if line search succeeded
    X = X+x3*s; f0 = f3; fX = [fX' f0]';                     % update variables
    fprintf('%s %6i;  Value %4.6e\r', S, i, f0);
    s = (df3'*df3-df0'*df3)/(df0'*df0)*s - df3;   % Polack-Ribiere 共轭梯度方向  搜索方向的更新公式
    df0 = df3;                                               % swap derivatives
    d3 = d0; d0 = df0'*s;
    if d0 > 0                                      % new slope must be negative
      s = -df0; d0 = -s'*s;                  % otherwise use steepest direction 负梯度方向
    end
    x3 = x3 * min(RATIO, d3/(d0-realmin));          % slope ratio but max RATIO
    ls_failed = 0;                              % this line search did not fail
  else
    X = X0; f0 = F0; df0 = dF0;                     % restore best point so far
    if ls_failed || i > abs(length)         % line search failed twice in a row
      break;                             % or we ran out of time, so we give up
    end
    s = -df0; d0 = -s'*s;                                        % try steepest
    x3 = 1/(1-d0);
    ls_failed = 1;                                    % this line search failed
  end
end
fprintf('\n');

4. 参考文献

[1]汪丹戎. 非线性共轭梯度法及全局收敛性分析[D].长江大学,2016.

[2] Quadratic and Cubic Search for a Minimum

[3] 2006, Carl Edward Rasmussen, Minimize

[4] 2011, Conjugate Gradient Back-propagation with Modified Polack Rebier updates for training feed forward neural network

[5] 景慧丽. 无约束最优化问题的算法研究与实现[D].西安科技大学,2009.

[6] 数值优化（Numerical Optimization）学习系列-线搜索方法（LineSearch）