洛谷P4551 最长异或路径

传送门：https://www.luogu.org/problem/show?pid=4551

在看这道题之前，我们应懂这道题怎么做：给定n个数和一个数m，求m和哪一个数的异或值最大。

一种很不错的做法是将n个数按二进制从最高位到低位建立一个trie树，然后把m放在trie树上跑一遍。

因为是从高位到低位存的，所以对于每一位，我们只要贪心让这一位的异或值得1。即如果m得当前位是1，就在trie树上找0；否则就找1.若能找到，ans的这一位就是1，否则是0.

如果上述这道水题会了的话，这道题就不难想了。

首先预处理每一个点到根节点的异或距离，为什么这么做呢，看下图

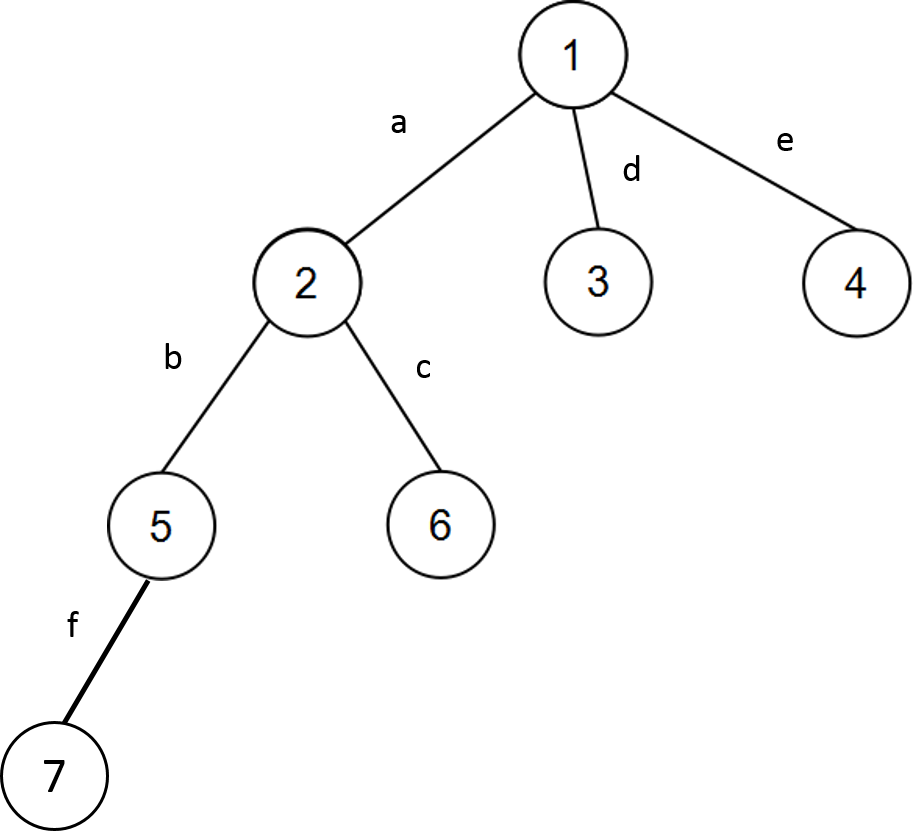
比如点7到根节点的距离dis[7] = f ^ b ^ a，点6到根节点的距离dis[6] = c ^ a，则dis[7] ^ dis[6] = f ^ b ^ c ^ a ^ a = f ^ b ^ c，恰好为6到7的距离。

因此我们就可以像上面这道题一样，将所有dis放到trie树里面，然后再让每一个dis[i]跑一遍trie树，最后结果取max即可。

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<queue>
 #include<vector>
 #include<cctype>    //isdigit
 using namespace std;
 typedef long long ll;
 #define enter printf("\n")
 const int maxn = 1e5 + ;
 const int INF = 0x3f3f3f3f;
 inline ll read() {
     ll ans = ;
     char ch = getchar(), last = ' ';
     while(!isdigit(ch)) {
         last = ch;
         ch = getchar();
     }
     while(isdigit(ch)) {
         ans = ans *  + ch - '';
         ch = getchar();
     }
     if(last == '-') ans = -ans;
     return ans;
 }
 inline void write(ll x) {
     if(x < ) {
         putchar('-');
         x = -x;
     }
     if(x == ) {
         putchar('');
         return;
     }
     int q[], N = ;
     q[] = ;
     while(x) {
         q[++N] = x % ;
         x /= ;
     }
     while(N) {
         putchar('' + q[N]);
         --N;
     }
 }

 int n;
 vector<int> v[maxn], c[maxn];
 int cost[maxn];
 bool vis[maxn];
 void bfs(int s) {                        //bfs预处理每一个点到根节点的距离
     queue<int> q;
     q.push(s);
     vis[s] = ;
     cost[s] = ;
     while(!q.empty()) {
         int now = q.front();
         q.pop();
         for(int i = ; i < (int)v[now].size(); ++i) {
             if(!vis[v[now][i]]) {
                 vis[v[now][i]] = ;
                 cost[v[now][i]] = cost[now] ^ c[now][i];
                 q.push(v[now][i]);
             }
         }
     }
 }
 struct Trie {
     int ch[maxn * ][], tot;
     Trie() {
         memset(ch, , sizeof(ch));
         tot = ;
     }
     void Insert(int x) {                //建树
         int now = ;
         for(int i = ; i >= ; --i) {
             int w = (x >> i) & ;
             if(!ch[now][w]) ch[now][w] = ++tot;
             now = ch[now][w];
         }
     }
     int query(int x) {
         int now = , ret = ;
         for(int i = ; i >= ; --i) {
             int w = (x >> i) & ;
             if(!ch[now][!w]) now = ch[now][w];
             else {
                 now = ch[now][!w];                //若和x这一位不同的边存在，就走这条边，同时ret的这一位标记成1
                 ret += ( << i);
             }
         }
         return ret;
     }
 } trie;

 int ans = ;

 int main() {
     n = read();
     for(int i = ; i < n; ++i) {
         int a = read(), b = read(), cost = read();
         v[a].push_back(b);
         c[a].push_back(cost);
         v[b].push_back(a);
         c[b].push_back(cost);
     }
     bfs();
     for(int i = ; i <= n; ++i)
         trie.Insert(cost[i]);
     for(int i = ; i <= n; ++i)
         ans = max(ans, trie.query(cost[i]));
     write(ans);
     enter;
     return ;
 }