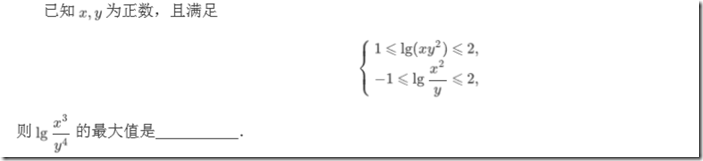
解答：3

评论：此类题目通性通法为换元后化归为线性规划问题。当然不等式凑配也是常见技巧，只是容易范围扩大或者缩小.

MT【27】对数方程组求范围的更多相关文章

  1. MT【73】求函数表达式

    评:由关系式求表达式最经典的莫过于已知$f(x+y)=f(x)f(y)$利用柯西法求得 $f(x)=[f(1)]^x$

  2. MT【266】求$a$的范围

    已知 $a$ 为常数,函数$f(x)=\dfrac{x}{\sqrt{a-x^2}-\sqrt{1-x^2}}$ 的最小值为$-\dfrac{2}{3}$,则 $a$ 的取值范围_____ 解: 考虑 ...

  3. MT【47】求一道分式的最值

    评:技巧性很大,需要敏锐的洞察力通过柯西不等式把分母变成一样.请记住这个变形$$(a+b+ab+1)=(a+1)(b+1)\le\sqrt{(a^2+1)(b^2+1)}$$

  4. wannafly 27 D 巧妙求取约数

    链接:https://www.nowcoder.com/acm/contest/215/D来源:牛客网 题目描述 “我不知道你在说什么,因为我只是个pupil.”--绿魔法师 一个空的可重集合S. n ...

  5. 机器学习-logistic对数回归求参数，画散点图以及分割线

    这个在我初学的时候我也不是很明白,于是在查了很多资料后找到一个很不错的博客给大家分享一下!! 研读一下代码对初学者有很大的帮助 作为一个初学者,一开始都是模仿别人的代码学会后就成为自己的东西了,相信你 ...

  6. 负对数似然(negative log-likelihood)

    negative log likelihood文章目录negative log likelihood似然函数(likelihood function)OverviewDefinition离散型概率分布 ...

  7. Hinge Loss、交叉熵损失、平方损失、指数损失、对数损失、0-1损失、绝对值损失

    损失函数(Loss function)是用来估量你模型的预测值 f(x) 与真实值 Y 的不一致程度,它是一个非负实值函数,通常用 L(Y,f(x)) 来表示.损失函数越小,模型的鲁棒性就越好. 损失 ...

  8. iOS中求出label中文字的行数和每一行的内容

    今天遇到一个需求,需要计算label中文字的行数.想了好久也没想到好的解决方法,就在网上找了下.结果发现一篇文章是讲这个的.这部分代码不但能够求出一个label中文字行数,更厉害的是能够求出每一行的内 ...

  9. （模板）poj1681 高斯消元法求异或方程组（无解、唯一解、多解）

    题目链接:https://vjudge.net/problem/POJ-1681 题意:类似于poj1222,有n×n的01矩阵,翻转一个点会翻转其上下左右包括自己的点,求最少翻转多少点能使得矩阵全0 ...

随机推荐

  1. LVDS时序分析

    LVDS时序分析 2012年05月07日 11:48:08 Walle 阅读数:3355 标签: 平台工作   最近在调试基于telechip平台的LVDS驱动,一开始对该平台的LVDS时序不是很了解 ...

  2. mac brew update 报错

    环境为mac, 总共报了三种错误. 对应三种不同的解法. 1.   第一种如下, 提示 1.8 的版本找不到 $ brew update /usr/local/bin/brew: /usr/local ...

  3. LINQ 如何动态创建 Where 子查询

    还是那句话,十年河东,十年河西,莫欺少年穷! 学无止境,精益求精... 今天探讨下如何构造动态的LINQ子查询 LINQ,相信大家都写过,很简单,下面以一个基本的范例说明下: namespace Co ...

  4. 【SDOI2017】数字表格

    题面 题解 这道题目还有一种比较有意思的解法. 定义一种运算\((\mathbf f\oplus\mathbf g)(x) = \prod\limits_{d\mid x}\mathbf f(d)^{ ...

  5. CentOS 7.2:Failed to start IPv4 firewall with iptables

    问题 系统是centos7.2,且已经安装了iptables服务,但是在执行启动命令后,却报了iptables服务无法正常启动的错误. 启动命令如下: systemctl start iptables ...

  6. SpringBoot日记——ElasticSearch全文检索

    看到标题的那一串英文,对于新手来说一定比较陌生,而说起检索,应该都知道吧. 这个ElasticSearch目前我们的首选,他主要有可以提供快速的存储.搜索.分析海量数据的作用.他是一个分布式搜索服务, ...

  7. Python3出现"No module named 'MySQLdb'"问题-以及使用PyMySQL连接数据库

    Python3 与 Django 连接数据库,出现了报错:Error loading MySQLdb module: No module named 'MySQLdb'.原因如下:在 python2 ...

  8. Codeforces Round #504 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final)-A-Single Wildcard Pattern Matching

    #include<iostream> #include<algorithm> #include<stdio.h> #include<string.h> ...

  9. D. Cutting Out

    ---恢复内容开始--- 链接 [https://codeforces.com/contest/1077/problem/D] 题意 给你n,k,n个数,找出长度为k,的子串(不需连续),使得该子串数 ...

  10. 08-java学习-数组-增强for循环-数组与方法-main函数参数

    数组定义和使用 数组与方法的结合使用 main函数传参