LG1912 [NOI2009]诗人小G

诗人小G

题目描述

小G是一个出色的诗人，经常作诗自娱自乐。但是，他一直被一件事情所困扰，那就是诗的排版问题。

一首诗包含了若干个句子，对于一些连续的短句，可以将它们用空格隔开并放在一行中，注意一行中可以放的句子数目是没有限制的。小G给每首诗定义了一个行标准长度（行的长度为一行中符号的总个数），他希望排版后每行的长度都和行标准长度相差不远。显然排版时，不应改变原有的句子顺序，并且小G不允许把一个句子分在两行或者更多的行内。在满足上面两个条件的情况下，小G对于排版中的每行定义了一个不协调度, 为这行的实际长度与行标准长度差值绝对值的P次方，而一个排版的不协调度为所有行不协调度的总和。

小G最近又作了几首诗，现在请你对这首诗进行排版，使得排版后的诗尽量协调（即不协调度尽量小），并把排版的结果告诉他。

输入输出格式

输入格式：

输入文件中的第一行为一个整数T，表示诗的数量。

接下来为T首诗，这里一首诗即为一组测试数据。每组测试数据中的第一行为三个由空格分隔的正整数N，L，P，其中：N表示这首诗句子的数目，L表示这首诗的行标准长度，P的含义见问题描述。

从第二行开始，每行为一个句子，句子由英文字母、数字、标点符号等符号组成（ASCII码33～127，但不包含'-'）。

输出格式：

于每组测试数据，若最小的不协调度不超过10^18，则第一行为一个数，表示不协调度。接下来若干行，表示你排版之后的诗。注意：在同一行的相邻两个句子之间需要用一个空格分开。

如果有多个可行解，它们的不协调度都是最小值，则输出任意一个解均可。若最小的不协调度超过10^18，则输出“Too hard to arrange”（不含引号）。每组测试数据结束后输出“--------------------”（不含引号），共20个“-”，“-”的ASCII码为45，请勿输出多余的空行或者空格。

输入输出样例

输入样例#1：
复制

4
4 9 3
brysj,
hhrhl.
yqqlm,
gsycl.
4 9 2
brysj,
hhrhl.
yqqlm,
gsycl.
1 1005 6
poet
1 1004 6
poet

输出样例#1：
复制

108
brysj,
hhrhl.
yqqlm,
gsycl.
--------------------
32
brysj, hhrhl.
yqqlm, gsycl.
--------------------
Too hard to arrange
--------------------
1000000000000000000
poet
--------------------

说明

【样例说明】

前两组输入数据中每行的实际长度均为6，后两组输入数据每行的实际长度均为4。一个排版方案中每行相邻两个句子之间的空格也算在这行的长度中（可参见样例中第二组数据）。每行末尾没有空格。

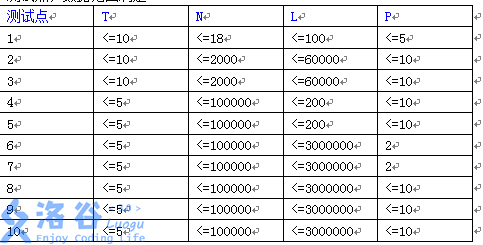
所有句子的长度不超过 $30$

分析

设F[i]表示前i句最小代价。记a[i]为第i句诗长度，s[i]表示前i句诗长度前缀和。

\[F[i]=\min_{0\le j < i}\{F[j]+|(s[i]-s[j])+(i-j-1)-L|^P\}
\]

枚举转移时间复杂度\(O(n^2)\)。这里，\(val(j,i)=|(s[i]-s[j])+(i-j-1)-L|^P\)，不能用单调队列或者斜率式来优化（所以这题暴力有50分）。于是尝试判断val(j,i)是否满足四边形不等式，即证明对于任意j<i，\(val(j,i+1)+val(j+1,i)\ge val(j,i)+val(j+1,i+1)\)，只需证明\(val(j+1,i)-val(j+1,i+1)\ge val(j,i)-val(j,i+1)\)

设u=(s[i]+i)-(s[j]+j)-(L+1)，即val(j,i)底数。

设v=(s[i]+i)-(s[j+1]+j+1)-(L+1)，即val(j+1,i)底数。

只需证明\(|v|^P-|v+(a[i+1]+1)|^P\ge|u|^P-|u+(a[i+1]+1)|^P\)

显然u>v，故只需证明对于任意正常数c，函数\(y=|x|^P-|x+c|^P\)单调递减。

1. \(p\equiv 1\ (\bmod 2),x\in[-c,0]​\)

   \[y=-x^P-(x+c)^P\\
   y'=-Px^{P-1}-P(x+c)^{P-1}< 0
   \]

2. \(p\equiv 1\ (\bmod 2),x\in[-\infty,-c]​\)

   \[y=-x^P+(x+c)^P\\
   y'=P(x+c)^{P-1}-Px^{P-1}<0
   \]

3. \(p\equiv 1\ (\bmod 2),x\in[0,\infty]\)

   \[y=x^P-(x+c)^P\\
   y'=Px^{P-1}-P(x+c)^{P-1}<0
   \]

4. \(p\equiv 0\ (\bmod 2)\)

   \[y=x^P-(x+c)^P\\
   y'=Px^{P-1}-P(x+c)^{P-1}<0
   \]

综上所述，val(j,i)满足四边形不等式。因此，F满足决策单调性。用队列维护三元组，即可在\(O(n \log n)\)时间内解决本题。

co int N=1e5+1;
int n,l,p;
char str[N][31];
int s[N],g[N];
ld f[N];
struct Q{int x,l,r;}q[N];
ld calc(int j,int i){
	return f[j]+pow(abs((ld)s[i]-s[j]+i-j-1-l),p); // edit 1: coercive transformation
}
void insert(int i,int&L,int&R){
	int w=-1;
	while(L<=R){
		if(calc(i,q[R].l)<=calc(q[R].x,q[R].l)) w=q[R--].l;
		else{
			if(calc(q[R].x,q[R].r)>calc(i,q[R].r)){
				int l=q[R].l,r=q[R].r;
				while(l<r){
					int mid=l+r>>1;
					if(calc(i,mid)>calc(q[R].x,mid)) l=mid+1;
					else r=mid;
				}
				q[R].r=l-1,w=l;
			}
			break;
		}
	}
	if(w!=-1) q[++R].x=i,q[R].l=w,q[R].r=n;
}
void G(){
	read(n),read(l),read(p);
	for(int i=1;i<=n;++i)
		scanf("%s",str[i]),s[i]=s[i-1]+strlen(str[i]);
	int L=1,R=1;
	q[1].x=0,q[1].l=1,q[1].r=n;
	for(int i=1;i<=n;++i){
		while(L<=R&&q[L].r<i) ++L;
		f[i]=calc(q[L].x,i),g[i]=q[L].x;
		insert(i,L,R);
	}
	if(f[n]>1e18) puts("Too hard to arrange");
	else{
		printf("%.0Lf\n",f[n]);
		stack<pair<int,int> > st;
		for(int i=n;i;i=g[i]) st.push(make_pair(g[i]+1,i));
		for(;st.size();st.pop())
			for(int i=st.top().first;i<=st.top().second;++i)
				printf("%s%c",str[i],i<st.top().second?' ':'\n');
	}
	puts("--------------------");
}
int main(){
	for(int t=read<int>();t--;) G();
	return 0;
}