网络游戏逆向分析-6-使用背包物品call

首先，大家在处理网络游戏的时候，一定得利用好发包函数，因为他就是整个网络游戏的关键。

处理办法：

这里还是直接给发包打断点来处理。

就像我们之前处理喊话函数call一样来处理它：

还是先给send打断点，然后依次往上找函数调用，直到只有使用背包物品才会断下来的函数作为关键函数分析：

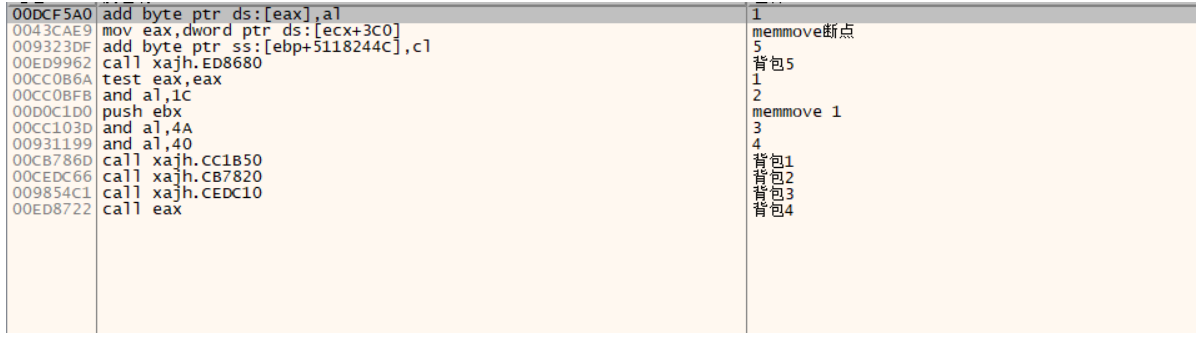
肯定会有重复的，重复的就直接继续往上跳就行了

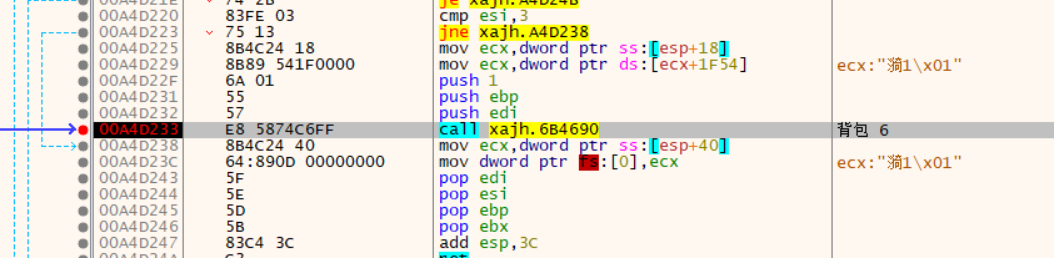
我在这个背包6这个函数这里就满足了所有要求：1：使用背包内容会断下来，2别的不会。所有我就把这个作为一个关键函数call来分析。

首先分析函数的参数，由于这是一个windows内部的函数，所以很有可能是stdcall 或者cdecall，就直接利用堆栈就好了，函数最后肯定会平栈的，不管前面有多少push，直接看函数执行完之后的栈提升就多少就可以大概看出来有多少参数：

现在是这样：

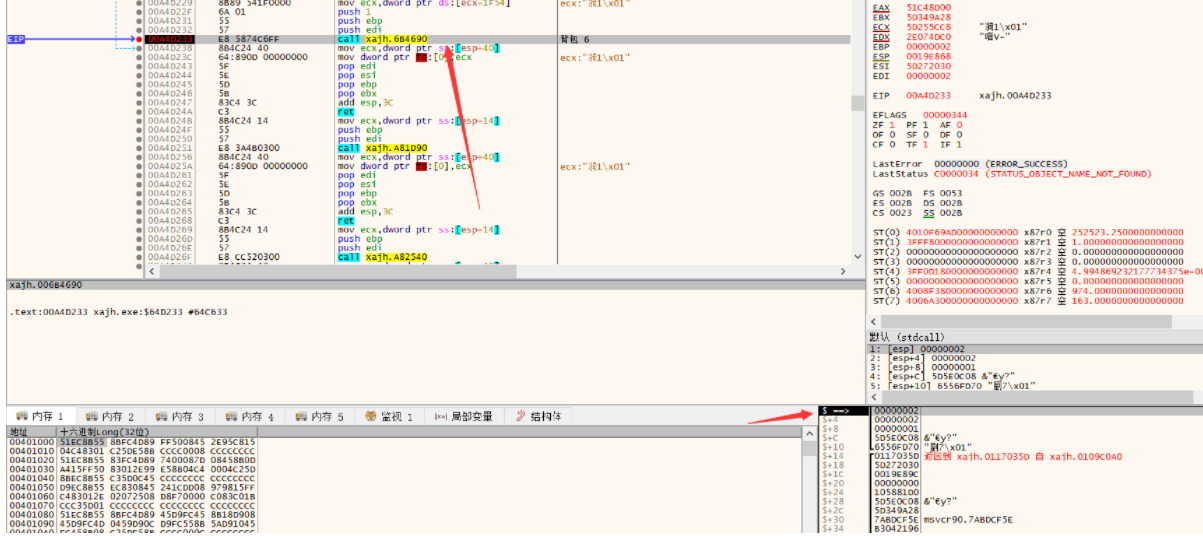
然后是这样：

+C，C就是12，应该是有3个参数在里面，还有需要注意的是ECX这个寄存器，在C++里面尤其要注意他，因为如果扯到了类里面的thiscall就会有一个ecx来存放this指针，所以这里分析的时候就带着它一起分析了。

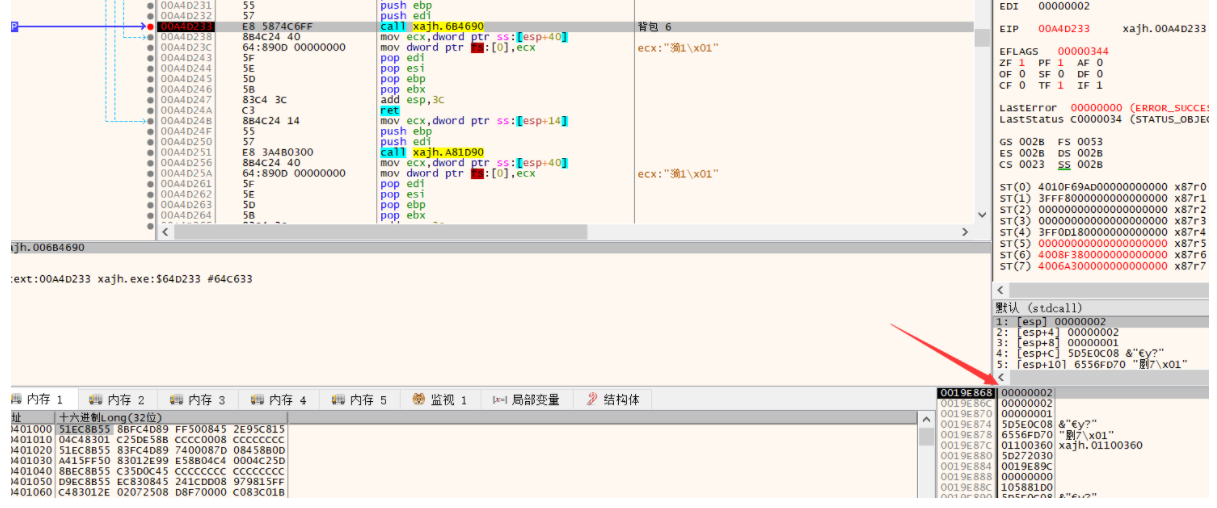
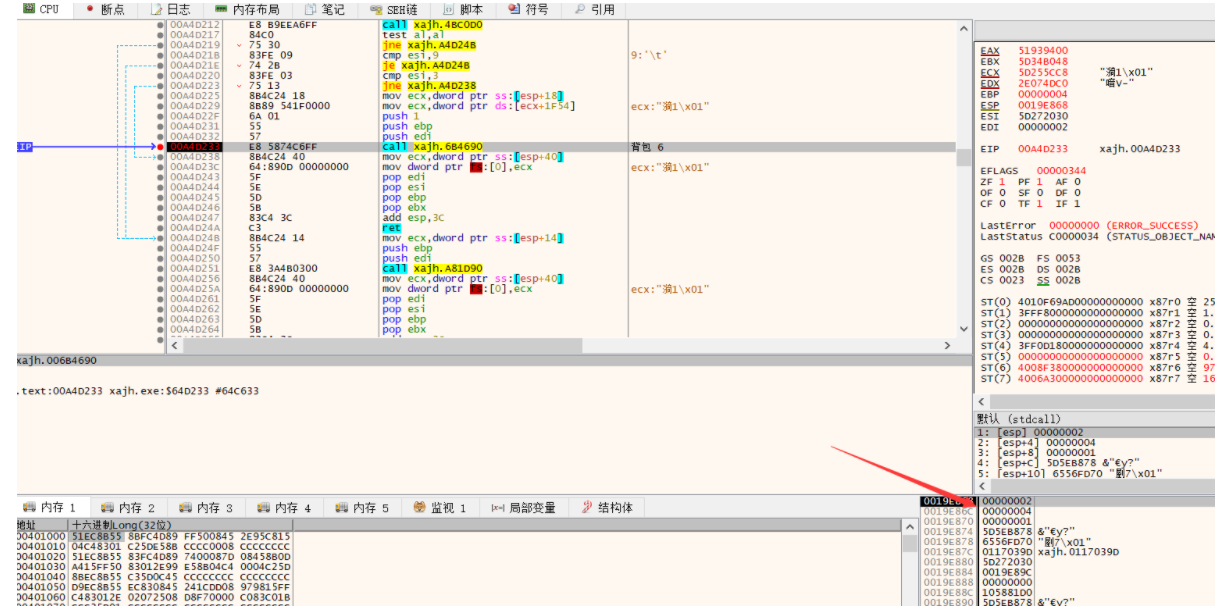
不管我用背包的哪一个，这个第一个参数的2和最后一个的1都没有改变过，而中间这个会随着物品的不同而改变不同，推测是根据物品的数组从0开始然后01234这样来处理：

果然再我用第六个物品的时候它变成了5：

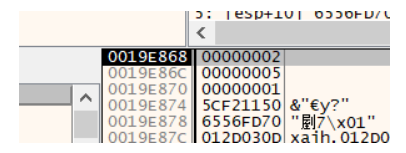
然后就是ecx里面的this指针了，这里先拿来用着：

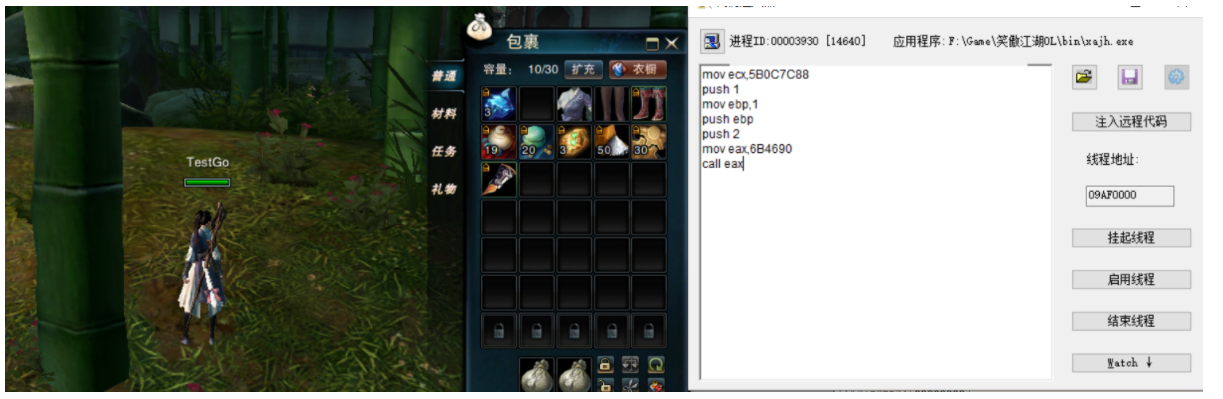
这里我第二个物品栏的东西被我吃完了，所以这里是肯定成功了。然后就来分析参数，其实也就一个ecx需要分析而已，别的都是固定的。

ecx是这样来的，是不是非常像先是ecx得到某个地址的首地址，然后偏移1F54得到了内容.

所以这里来分析mov ecx,....[esp+18]。

前面我们说到过牵扯到esp的就首先考虑参数，临时变量这种东西。首先考虑参数，利用Windows调用函数的极值，是先把参数入栈，然后再把返回地址入栈来看是不是参数：

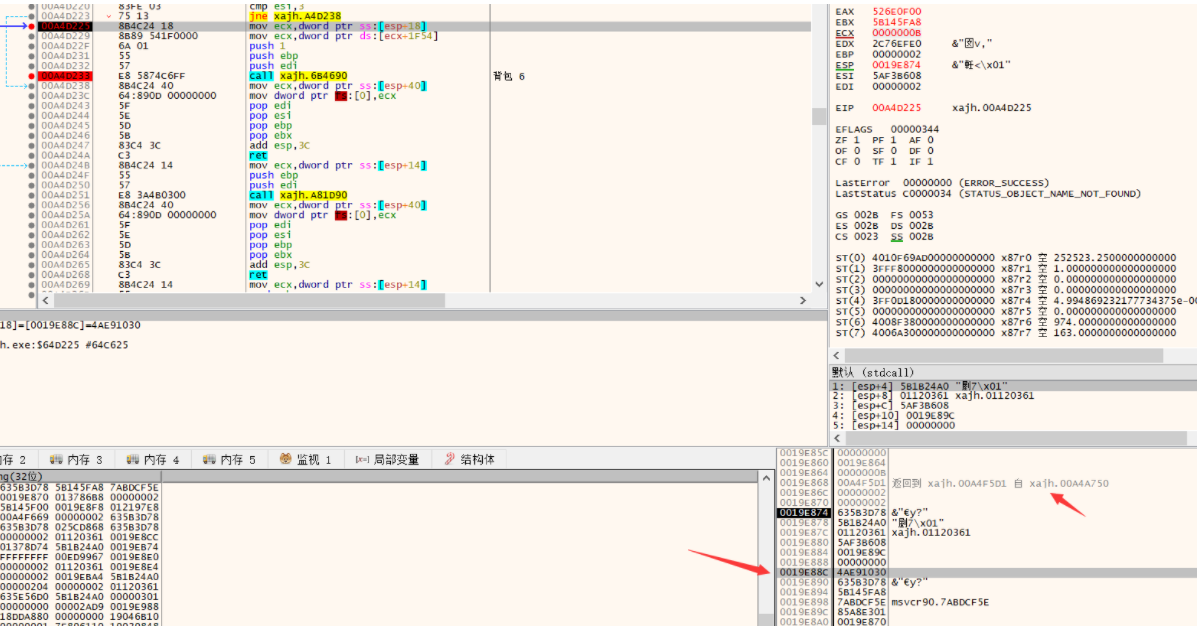
可以看到这个地址离返回的地址相当的远啊，所以很有可能就不是参数，这里我们再考虑，将函数跳出后看参数堆栈有没有被释放来判断是否是参数：

刚开始：

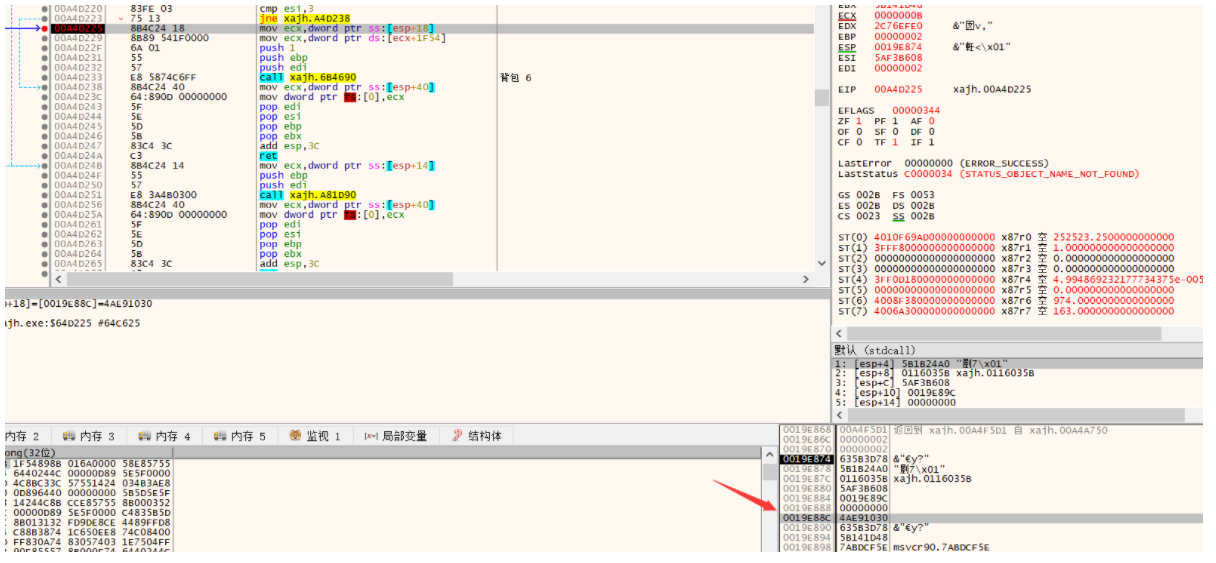
跳出函数后：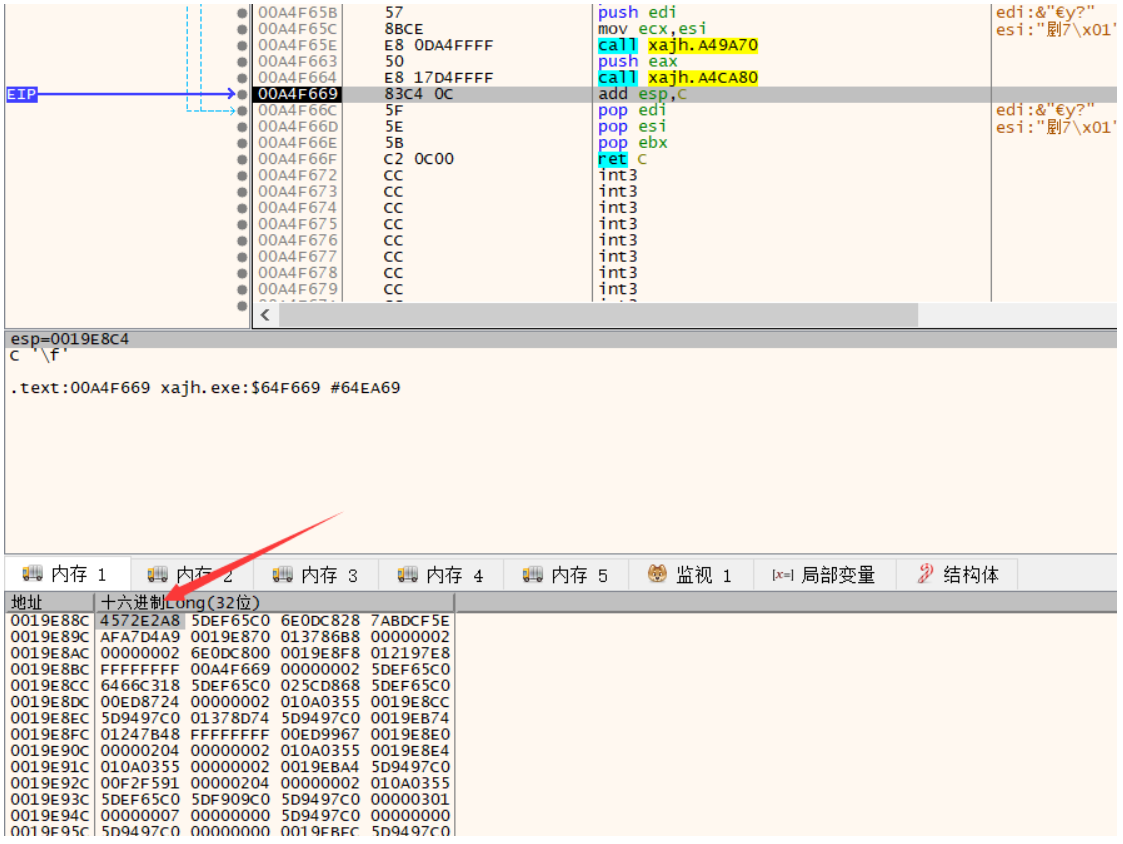

丝毫没有改变，说明它不是这个函数的参数。

很有可能是一个局部变量，局部变量的验证就比较方便了，在函数的头部断下来，然后打一个硬件断点，修改了就断下来，前提是这个函数的esp+18这个地址不会改变（这个自己去验证）。这里我直接操作了

在函数第一条地址下断下来，然后打一个硬件写入断点，段下来后在这里：

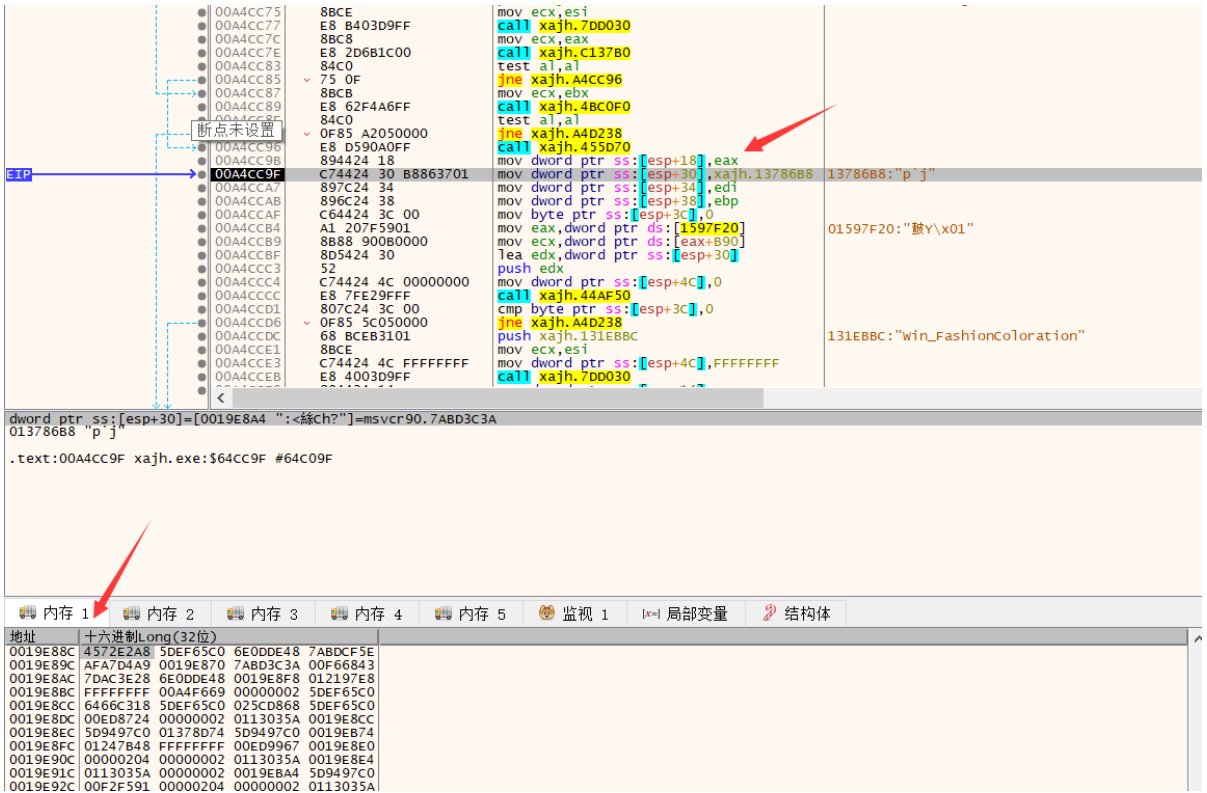
这样就一目了然，是被这里的eax给修改了，就分析这个eax就行了。

这个eax前面正好有一个函数调用，来分析看看是不是这个函数的问题，先给函数的上一条指令打断点来分析eax：

先是为0

调用完之后就是这个值了：

直到要调用背包的时候这个值依然是这个值：

因为前面是eax来修改了[esp+18]地址对应的内容

所以一直这样下来没问题。而且这个修改eax的函数根本没有参数调用，所以可以直接拿来用：

这样的话就我们的代码逻辑就成型了：

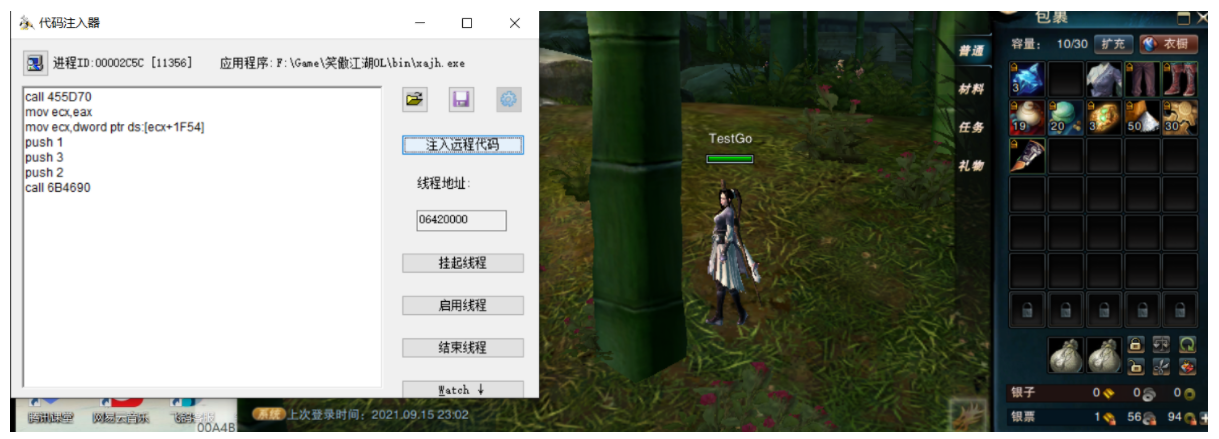
这里的call函数，就是把eax赋值为后面的mov ecx,dword ptr ss[esp+18]给代替了，

然后push 1 push2是必须的，中间的push 3是物品在物品栏中的位置，最后的call函数是调用背包的函数。

总结

大型网络游戏，发包函数是非常非常重要的，通过发包函数可以贯彻到很多东西，对于ESP这个寄存器必须要考虑到函数参数和临时变量，根据是参数还是临时变量来分别使用分析方法，参数就可以直接看，然后临时变量采用硬件断点来查看修改。区分是不是参数可以通过将函数执行完后的栈是否将其舍弃掉来判断，因为参数是函数栈里面的函数调用完之后就会释放这个栈。

这里还有不合理的地方，如果外挂给别人用，别人肯定是想输入一个名字，比如说蓝药水就直接用了，这个还要人家来数数组，肯定垃圾不行，所有后面还要来遍历数组来获取对应的内容。