算法：杨辉三角（Pascal's Triangle）

一、杨辉三角介绍

　　杨辉三角形，又称帕斯卡三角形、贾宪三角形、海亚姆三角形、巴斯卡三角形，是二项式系数的一种写法，形似三角形，在中国首现于南宋杨辉的《详解九章算法》得名，书中杨辉说明是引自贾宪的《释锁算书》，故又名贾宪三角形。在那之前，还有更早发现这个三角的波斯数学家和天文学家，但相关的内容没有以图文保存下来，所以中国的数学家对此研究有很大贡献。

　　　　　　　　１
　　　　　　　１　１
　　　　　　１　２　１
　　　　　１　３　３　１
　　　　１　４　６　４　１
　　　１　５　10　10　５　１
　　１　６　15　20　15　６　１
　１　７　21　35　35　21　７　１
１　８　28　56　70　56　28　８　１

　　以上是杨辉三角的前 9 行，可以看出来每一行的所有数字对应着二项式 (A+B)ⁿ 的展开式系数，这里 n 从第 0 行开始。

二、杨辉三角的一些性质与实现

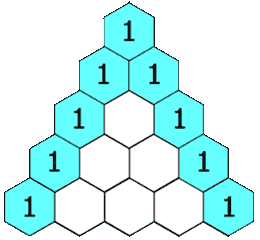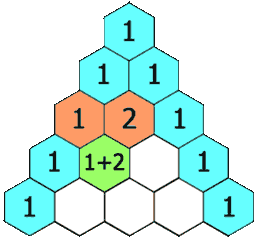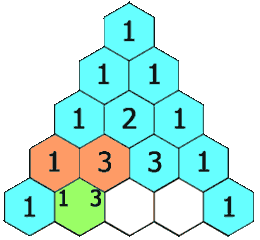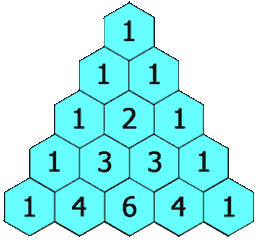
此三角形的性质有（注：最顶的 1 处于第 0 行）：

• 由正整数构成，每一行的数字左右对称；

• 第（2的幂）行都是奇数；

• 每一行数字之和都是2的幂；

• 第N行数字个数都是N；

• 第N行的第K个数字为组合数；

• 除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和（也就是说，第 N 行第 K 个数字等于第 N-1 行的第 K-1 个数字与第 K 个数字的和）。

　　因而固有恒等式：

　　　　    

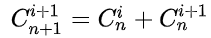
　　可用此性质写出整个杨辉三角形。

 1     /**
 2      * 杨辉三角与 (a+b)^n 二项式系数的展开
 3      *
 4      * @param n
 5      * @param k
 6      * @return
 7      */
 8     private static int binomialCoefficient(int n, int k) {
 9         int res = 1;
10         if (k > n - k) {
11             k = n - k;
12         }
13         for (int i = 0; i < k; i++) {
14             res *= (n - i);
15             res /= (i + 1);
16         }
17         return res;
18     }

　　打印杨辉三角的函数：

 1     /**
 2      * 打印杨辉三角
 3      *
 4      * @param n
 5      */
 6     private static void printPascal(int n) {
 7         for (int line = 0; line < n; line++) {
 8             for (int i = 0; i <= line; i++) {
 9                 System.out.print(binomialCoefficient(line, i) + " ");
10             }
11             System.out.println();
12         }
13     }

　　算法的时间复杂度大致为 O(N³)，这里 N 为所打印杨辉三角的行数。