Luogu P2149 [SDOI2009]Elaxia的路线 | 图论

题目链接

题解：

题面中给了最简洁清晰的题目描述：“求无向图中，两对点间最短路的最长公共路径”。

对于这个问题我们可以先考虑图中的哪些边对这两对点的最短路产生了贡献。

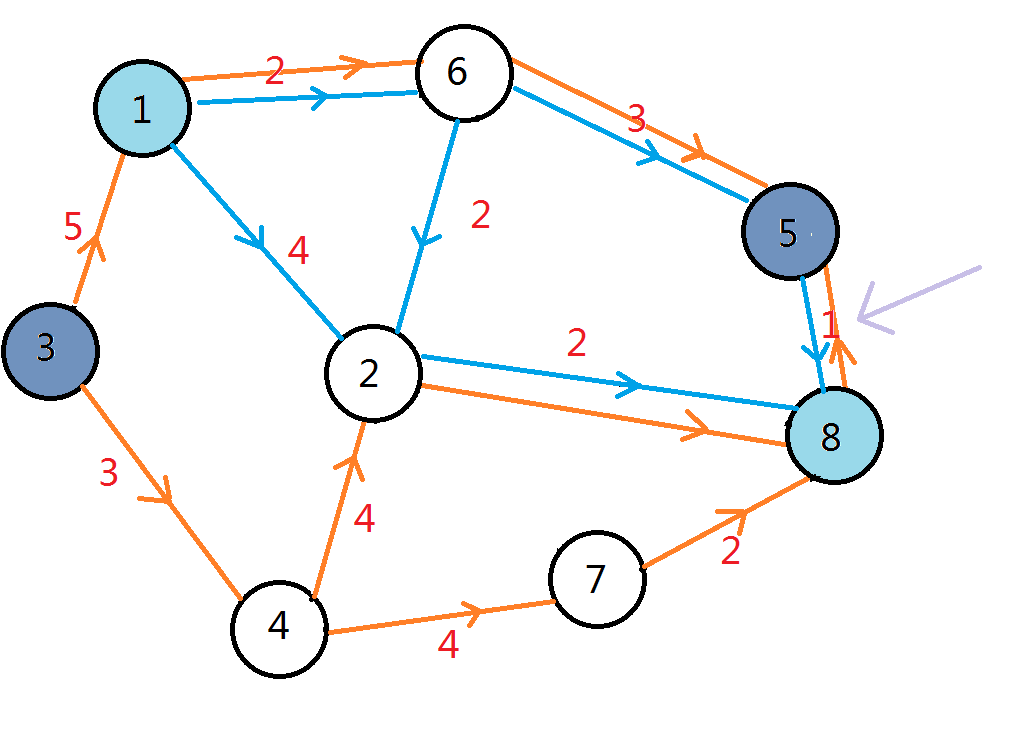
比如说下面这个图：

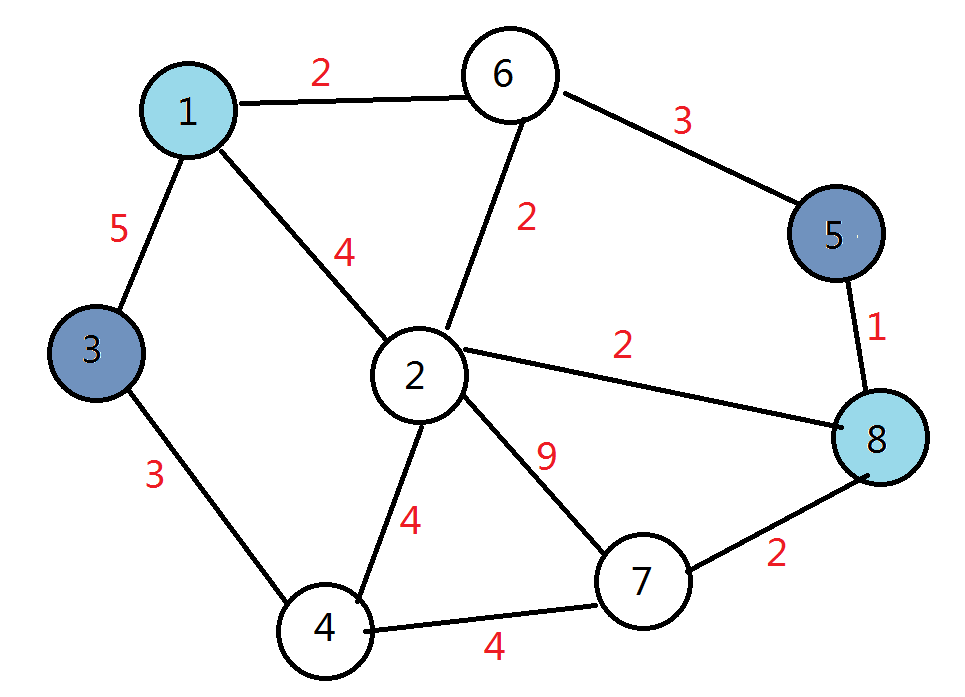
我们要求从1到8的最短路和从3到5的最短路的最长公共路径。

先考虑有哪些边对从1到8的最短路产生了贡献，并按这些边被经过时的方向构造一个有向图。

如下：

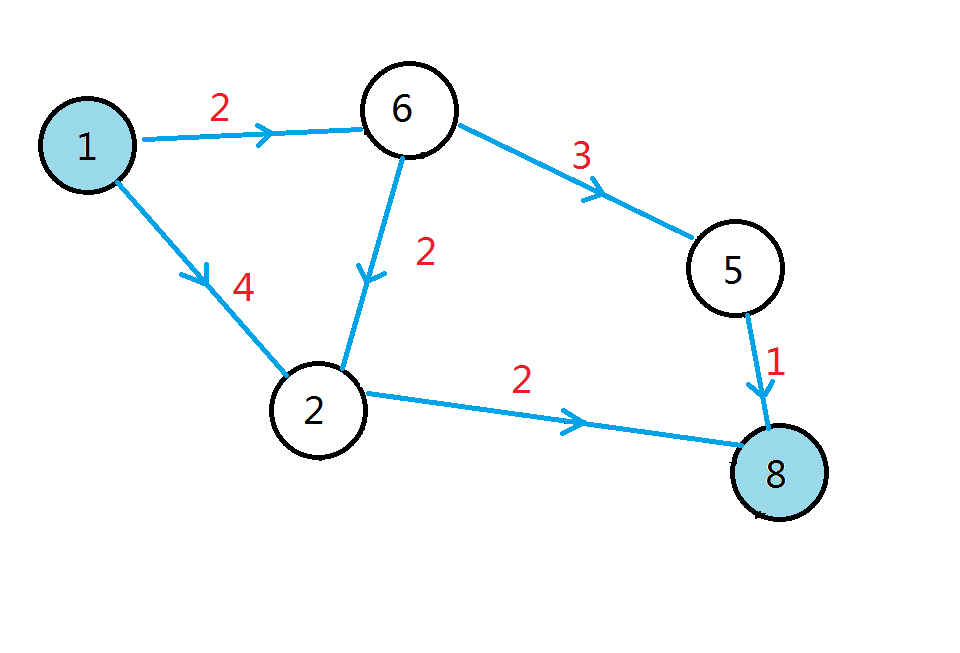
然后再考虑有哪些边对从3到5的最短路产生了贡献，然后也按这些边被经过时的方向构造一个有向图。

如下：

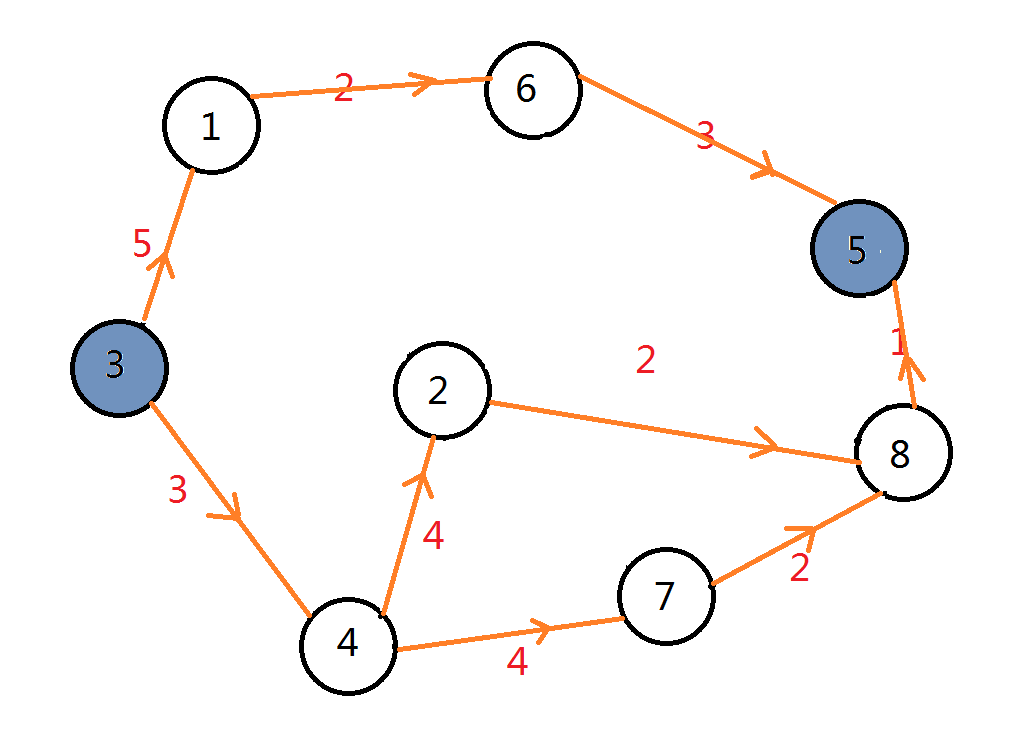
我们知道，这两对点间最短路的最长公共路径一定在上述两张有向图的重叠部分中。

于是我们可以试着将那两张有向图重叠起来：

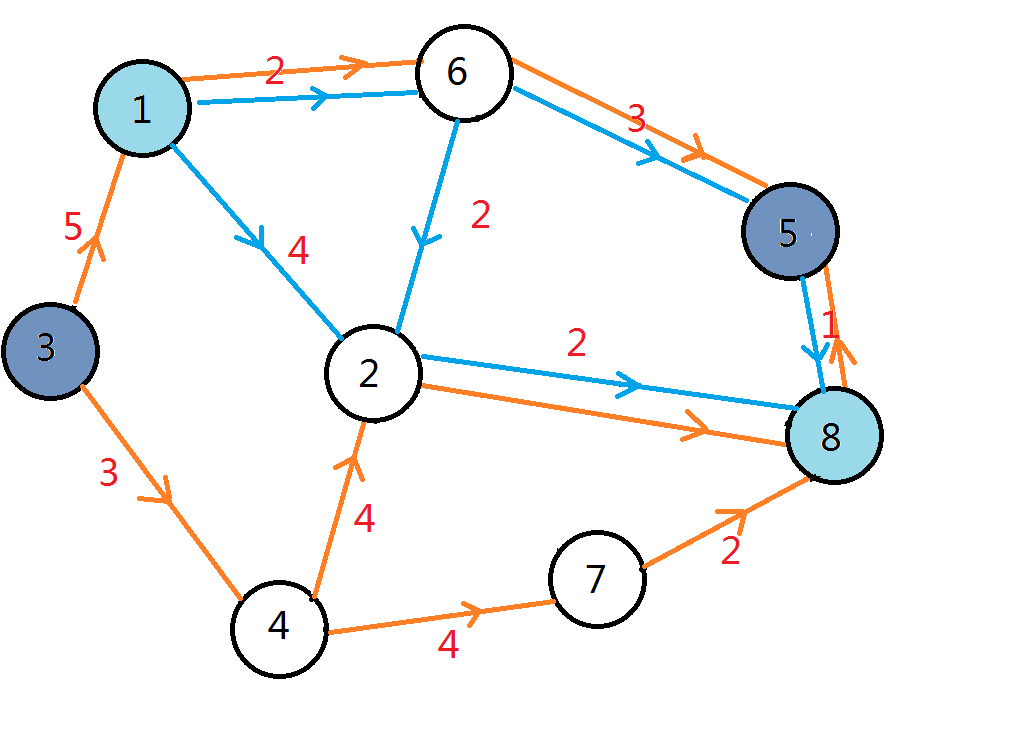
接着提取其中的公共部分：

由于我们一开始构造的两张图都一定是有向无环图（想想为什么），所以它们的公共部分也一定是若干张有向无环图。

又因为两点间的最短路一定是一条链，所以两条最短路的公共部分也一定是一条链。

这样的话，我们的任务就变成了在这若干张有向无环图中求最长链。

这个问题可以用dp在O(n)的时间内解决。

那么如何我们该如何构造一开始的两张有向图呢？这可以用SPFA解决。

对于每个点，都记录它是从哪个点走过来的，最后从终点倒推回去即可。

值得注意的是，我们不能只对其中一对点的一个点构造有向图。因为在最短路上走的方向可能是不同的，如果只构造一张图的话就会漏掉行走方向不同的边。

像上面我们举的那个例子，这条边就没有被算进去，但它其实也是这两对点间最短路的公共部分。

那么我们能不能直接忽略图的方向呢？

不行，因为如果直接忽略图的方向的话，我们得出来的答案可能会属于一对点之间的两条不同的最短路（想想为什么）。

对此，我们可以对其中一对点的最短路正着构造出一个有向图，反着再构造出一个有向图，然后将它们分别与对另一对点的最短路构造的有向图进行相应的操作即可。

比如说上面所举的那个例子，我们先对结点1到结点8的最短路构造一个有向图（称为图1），然后再分别对结点3到结点5的最短路和结点5到结点3的最短路构造一个有向图（分别称为图2和图3）。最后，我们先拿图1和图2做一次那样的操作，然后再拿图1和图3做一次那样的操作即可。（“那样的操作”是指提取公共部分和dp求最长链。）

总时间复杂度为O(nm+n²+n)，其中的nm是SPFA在最坏情况下的时间复杂度，n²是提取两张有向图公共部分的时间复杂度，n是dp求最长链的时间复杂度。

这个时间复杂度虽然理论上来说是不能过的，但在实际测试中，SPFA的时间复杂度是低于O(nm)的上限的，所以这是能过的。

大家也可以用使用堆优化的dijkstra算法来代替SPFA，以换取在求最短路时O(nlog₂n)的稳定时间复杂度。

提取两张有向图公共部分的时间其实也是可以优化的，但这个实现起来较为简单，就不再赘述了。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
    using namespace std;
    int n=0,m=0,x1=0,y1=0,x2=0,y2=0,ans=0,head=0,tail=0;
    //last[i][j]=1表示编号为i的结点可以从编号为j的结点走过来
    int d[1505],k[1505],dis[1505],book[1505],que[2265025],last[1505][1505],f[1505][1505],s[1505][1505],h[1505][1505],p[1505][1505];
void SPFA(int s)//SPFA
{
    head=1,tail=0;
    for(int i=1;i<=n;i++) dis[i]=1e8,book[i]=k[i]=0;
    dis[s]=0;
    que[++tail]=s;
    book[s]=1;
    while(head<=tail)
    {
        int u=que[head++];
        book[u]=false;
        for(int i=1;i<=n;i++)
        {
            if(i==u) continue;
            if(dis[u]+f[u][i]<dis[i])
            {
                dis[i]=dis[u]+f[u][i];
                k[i]=1;
                last[i][k[i]]=u;//更新last数组
                if(book[i]==false)
                {
                    que[++tail]=i;
                    book[i]=true;
                }
            }
            else if(dis[u]+f[u][i]==dis[i]) last[i][++k[i]]=u;//更新last数组
        }
    }
}
void work(int x,int h[][1505])//构造对最短路有贡献的边所组成的有向图
{
    if(book[x]==1) return;
    book[x]=1;
    for(int i=1;i<=k[x];i++)
    {
        h[last[x][i]][x]=1;
        work(last[x][i],h);
    }
}
void dp(int x)//dp求有向无环图最长链
{
    if(d[x]>0) return;
    for(int i=1;i<=n;i++)
        if(p[x][i]==1)
        {
            dp(i);
            d[x]=max(d[x],d[i]+f[x][i]);
        }
}
int main()
{
    scanf("%d%d%d%d%d%d",&n,&m,&x1,&y1,&x2,&y2);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            f[i][j]=(i==j)?0:1e8;
    for(int i=1;i<=m;i++)
    {
        int u=0,v=0,w=0;
        scanf("%d%d%d",&u,&v,&w);
        f[u][v]=f[v][u]=min(f[u][v],w);//邻接矩阵存图
    }
    //对从x1到y1的最短路进行处理
    SPFA(x1);
    memset(s,0,sizeof(s));
    memset(book,0,sizeof(book));
    work(y1,s);
    //对从x2到y2的最短路进行处理
    SPFA(x2);
    memset(h,0,sizeof(h));
    memset(book,0,sizeof(book));
    work(y2,h);
    //提取两张有向图的公共部分
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(s[i][j]==1&&h[i][j]==1) p[i][j]=1;
                                  else p[i][j]=0;
    //dp求最长链
    memset(d,0,sizeof(d));
    for(int i=1;i<=n;i++)
        if(d[i]==0) dp(i);
    for(int i=1;i<=n;i++) ans=max(ans,d[i]);
    //对从y2到x2的最短路进行处理
    SPFA(y2);
　　 memset(h,0,sizeof(h));
    memset(book,0,sizeof(book));
    work(x2,h);
    //提取两张有向图公共部分
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(s[i][j]==1&&h[i][j]==1) p[i][j]=1;
                                  else p[i][j]=0;
    //dp求最长链
    memset(d,0,sizeof(d));
    for(int i=1;i<=n;i++)
        if(d[i]==0) dp(i);
    for(int i=1;i<=n;i++) ans=max(ans,d[i]);
    //输出
    printf("%d",ans);
    return 0;
}