状压DP详解+题目

介绍

状压dp其实就是将状态压缩成2进制来保存 其特征就是看起来有点像搜索，每个格子的状态只有1或0 ，是另一类非常典型的动态规划

举个例子：有一个大小为n*n的农田，我们可以在任意处种田，现在来描述一下某一行的某种状态：

设n = 9；

有二进制数 100011011（九位），每一位表示该农田是否被占用，1表示用了，0表示没用，这样一种状态就被我们表示出来了：见下表

位运算

为了更好的理解状压dp，首先介绍位运算相关的知识。

& 符号，x&y，会将两个十进制数在二进制下进行与运算(都1为1，其余为0） 然后返回其十进制下的值。例如3(11)&2(10)=2(10)。

|符号，x|y，会将两个十进制数在二进制下进行或运算（都0为0，其余为1） 然后返回其十进制下的值。例如3(11)|2(10)=3(11)。

^ 符号，x^y，会将两个十进制数在二进制下进行异或运算（不同为1，其余 为0）然后返回其十进制下的值。例如3(11)^2(10)=1(01)。

 ~ 符号，~x，按位取反。例如~101=010。

<< 符号，左移操作，x<<2，将x在二进制下的每一位向左移动两位，最右边用0填充，x<<2相当于让x乘以4。 ’>>’符号，是右移操作，x>>1相当于给x/2，去掉x二进制下的最右一位

1.判断一个数字x二进制下第i位是不是等于1。（最低第1位）
方法：if(((1<<(i−1))&x)>0) 将1左移i-1位，相当于制造了一个只有第i位 上是1，其他位上都是0的二进制数。然后与x做与运算，如果结果>0， 说明x第i位上是1，反之则是0。

2.将一个数字x二进制下第i位更改成1。   方法：x=x|(1<<(i−1)) 证明方法与1类似。

3.将一个数字x二进制下第i位更改成0。   方法：x=x&~(1<<(i−1))

4.把一个数字二进制下最靠右的第一个1去掉。   方法：x=x&(x−1)

题目

P1896 [SCOI2005]互不侵犯

一道很好的状压dp题。

由于每个格子只有两种状态：放国王 和 不放国王 ，用 1 表示放国王，0 表示不放国王；那么把每个格子的数连起来就是 \(（101001）_2\) ，这个数在十进制下是： \((101001)_2\)​ = \((41)_{10}\) ​

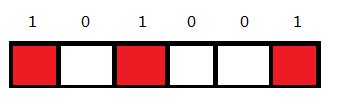
所以状压 dp 的套路就是不断的去枚举表示状态的数，去转移即可。

状态设置：

按照状压 dp 的套路，我们设状态：dp[i][S][j] 表示我们已经选到了第 i 行，第 i 行的状态为 S，用了 j 个国王的方案数；

首先看一下国王的攻击范围（以其为中心的九宫格）：红色代表国王位置，蓝色代表它的攻击范围：

思考：如果我们第 i−1 行的第 j 列放好国王之后，那么对第 i 行的影响是什么呢？也就是国王在第 i 行上的攻击范围内的格子不能再放国王了：

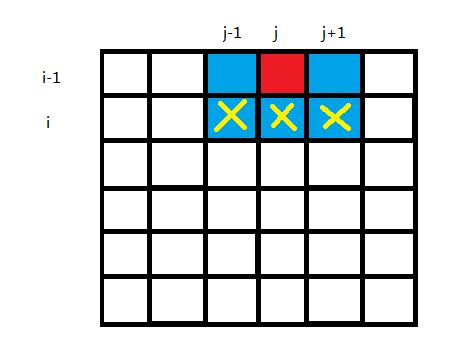
也就是说，如果第i−1 行的状态S1​（表示状态的二进制数）的第 j 位是 1（放国王）的话，第 i 行的状态 S2​ 的第 j−1，j，j+1 位一定为 0（不能再放国王了），否则就是不合法的状态；

所以我们就得出了表示这三个位置的方法，那么 S2​ 必须满足什么条件才可能由 S1​ 转移过去呢？

这是需要位运算了>_<!

条件：\((S2​ & S1​ ==0) && ( (S2​<<1) & S1​==0) && ( (S2​>>1) & S1​==0)\)

我们发现这样写有点长，还可以这样写：\((S2​∣(S2​>>1)∣(S2​<<1)) &S1​==0\)

当然，我们处理完行间的限制后，接下来就要处理行内的限制了；

一个国王的左右格子内不能再放国王了，这就是行内的限制！

直接上 \(((S2​<<1) & S2​==0) && ((S2​>>1) & S2​==0)\)（更简洁：\(((S2​<<1) & S2​==0) && ((S2​>>1) & S2​==0)\)）

最后就是普通的dp了

#include <bits/stdc++.h>
using namespace std;
int n,k;
long long cnt[1005],ok[1005];
int h=0;
long long f[15][1005][105];
int main(){
	scanf("%d%d",&n,&k);
	for (int s=0;s<(1<<n);s++){
		if (((s<<1)|(s>>1))&s)continue;
		int tot=0;
		for (int j=0;j<n;j++)
			if (s&(1<<j)) tot++;
		cnt[++h]=tot;
		ok[h]=s;
	}
	f[0][1][0]=1;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=h;j++)
			for (int l=cnt[j];l<=k;l++)
				for (int t=1;t<=h;t++){
					if (!(ok[t]&ok[j])&&!(ok[t]&(ok[j]<<1))&&!(ok[t]&(ok[j]>>1))){
						f[i][j][l]+=f[i-1][t][l-cnt[j]];
					}
				}
	long long ans=0;
	for (int i=1;i<=h;i++)	ans+=f[n][i][k];
	printf("%lld",ans);
	return 0;
}

P1879 [USACO06NOV]Corn Fields G

和上题差不多

也是有两个条件

1.田是否可以种

2.种的地方上下左右不能种

判断好之后，上代码

#include <bits/stdc++.h>
#define MOD 1000000000
using namespace std;
int m,n;
int F[15];
int a[15][15];
int f[15][5005];
bool cnt[5005];
int h=0;
int ans;

int main(){
	scanf("%d%d",&m,&n);
	for (int i=1;i<=m;i++){
		for (int j=1;j<=n;j++){
			scanf("%d",&a[i][j]);
			F[i]=(F[i]<<1)+a[i][j];
		}
	}
	for (int s=0;s<(1<<n);s++)
		cnt[s]=((s&(s<<1))==0)&&((s&(s>>1))==0);
	f[0][0]=1;
	for (int i=1;i<=m;i++){
		for (int l=0;l<(1<<n);l++){
			if (cnt[l]&&((l&F[i])==l)){
				for (int s=0;s<(1<<n);s++){
					if (!(l&s))
						f[i][l]=(f[i][l]+f[i-1][s])%MOD;
				}
			}
		}
	}
	for (int i=0;i<(1<<n);i++){
		ans+=f[m][i];
		ans%=MOD;
	}
	printf("%d\n",ans);
	return 0;
}

P2704 [NOI2001] 炮兵阵地

可以说是上一题的plus。

只要多加一次的循环就可以了

由于觉得太烦就先把1行2行先处理一下

#include <bits/stdc++.h>
using namespace std;
int n,m;
int f[105][105][105],l[105];
int a[105][105];
int h[505];
int num[505];
int cnt=1;
int main(){
	char s;
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++){
		for (int j=1;j<=m;j++){
			cin>>s;
			if (s=='H')	a[i][j]=1;
			l[i]=(l[i]<<1)+a[i][j];
		}
	}

	for (int i=1;i<(1<<m);i++){
		if ((((i<<2)|(i>>2)|(i<<1)|(i>>1))&i)==0){
			h[++cnt]=i;
			int s=i;
			while (s){
				num[cnt]++;
				s -= s & (-s);
			}
		}
	}

	for (int i=1;i<=cnt;i++)
		if ((h[i]&l[1])==0)
			f[1][i][0]=num[i];

	for (int i=1;i<=cnt;i++)
		if ((h[i]&l[2])==0)
			for (int j=1;j<=cnt;j++)
				if ((h[i]&h[j])==0&&(h[j]&l[1])==0)
					f[2][i][j]=f[1][j][0]+num[i];

	for (int i=3;i<=n;i++){
		for (int k1=1;k1<=cnt;k1++){
			if ((h[k1]&l[i])==0){
				for (int k2=1;k2<=cnt;k2++){
					if ((h[k1]&h[k2])==0&&(h[k2]&l[i-1])==0){
						for (int k3=1;k3<=cnt;k3++){
							if ((h[k1]&h[k3])==0&&(h[k2]&h[k3])==0&&(h[k3]&l[i-2])==0){
								f[i][k1][k2]=max(f[i][k1][k2],f[i-1][k2][k3]+num[k1]);
							}
						}

					}
				}

			}
		}
	}
	int ans=0;
	for (int i=1;i<=cnt;i++){
		for (int j=1;j<=cnt;j++){
			ans=max(ans,f[n][i][j]);
		}
	}
	printf("%d\n",ans);
	return 0;
}