使用numba加速python科学计算

技术背景

python作为一门编程语言，有非常大的生态优势，但是其执行效率一直被人诟病。纯粹的python代码跑起来速度会非常的缓慢，因此很多对性能要求比较高的python库，需要用C++或者Fortran来构造底层算法模块，再用python进行上层封装的方案。在前面写过的这篇博客中，介绍了使用f2py将fortran代码编译成动态链接库的方案，这可以认为是一种“事前编译”的手段。但是本文将要介绍一种即时编译（Just In Time，简称JIT）的手段，也就是在临近执行函数前，才对其进行编译。以下截图来自于参考链接4，讲述了关于常见的一些编译场景的区别：

用numba.jit加速求平方和

numba中大部分加速的函数都是通过装饰器（decorator）来实现的，关于python中decorator的使用方法和场景，在前面写过的这篇博客中有比较详细的介绍，让我们直接使用numba的装饰器来解决一些实际问题。这里的问题场景是，随便给定一个数列，在不用求和公式的情况下对这个数列的所有元素求平方和，即：

\[f(a)=\sum_ia_i^2
\]

我们已知类似于这种求和的形式，其实是有很大的优化空间的，相比于直接用一个for循环来求解的话。这里我们直接展示一下案例代码：

# test_jit.py

from numba import jit
import time
import matplotlib.pyplot as plt

def adder(max): # 普通的循环求解
    s = 0
    for i in range(max):
        s += i ** 2
    return s

@jit(nopython=True)
def jit_adder(max): # 使用即时编译求解
    s = 0
    for i in range(max):
        s += i ** 2
    return s

if __name__ == '__main__':
    time_adder = []
    time_jit_adder = []
    x = list(range(1, 10000000, 500000))
    for i in x:
        time1 = time.time()
        s = adder(i)
        time2 = time.time()
        s = jit_adder(i)
        time3 = time.time()
        time_adder.append(time2 - time1)
        time_jit_adder.append(time3 - time2)
    # 开始作图
    fig, ax1 = plt.subplots()
    color = 'black'
    ax1.set_xlabel('Numbers')
    ax1.set_ylabel('Time (s)', color=color)
    ax1.plot(x[1:], time_adder[1:], color=color, label='python')
    ax1.tick_params(axis='y', labelcolor=color)

    ax2 = ax1.twinx() # 第二个y-坐标轴
    color = 'red'
    ax2.set_ylabel('Time (s)', color=color)
    ax2.plot(x[1:], time_jit_adder[1:], color=color, label='jit')
    ax2.tick_params(axis='y', labelcolor=color)
    plt.title('Running time difference via using jit')

    fig.tight_layout()
    plt.legend()
    plt.savefig('jit.png')

运行该python文件，会在当前目录下产生一个双坐标轴的图像：



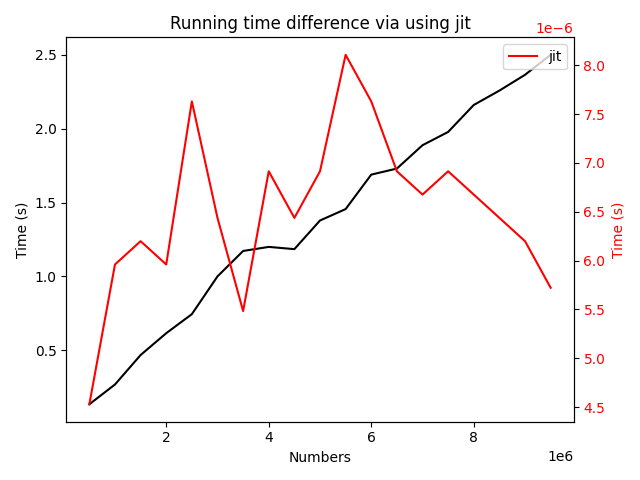
在这个计算结果中，使用了即时编译技术之后，求解的时间几乎被压缩到了微秒级别，而循环求和的方法却已经达到了秒级，加速倍数在\(10^5\)级别。

用numba.jit加速求双曲正切函数和

在上一个案例中，也许涉及到的计算过于的简单，导致了加速倍数超出了想象的情况。因此这里我们只替换所求解的函数，看看加速的倍数是否会发生变化。这里我们采用了双曲正切求和的函数：

\[f(a)=\sum_i\frac{e^{a_i}-e^{-a_i}}{e^{a_i}+e^{-a_i}}
\]

通过math来实现这个函数的计算，用以替换上一章节中求平方值的方法：

# test_jit.py

from numba import jit
import time
import matplotlib.pyplot as plt
import math

def adder(max):
    s = 0
    for i in range(max):
        s += math.tanh(i ** 2)
    return s

@jit(nopython=True)
def jit_adder(max):
    s = 0
    for i in range(max):
        s += math.tanh(i ** 2)
    return s

if __name__ == '__main__':
    time_adder = []
    time_jit_adder = []
    x = list(range(1, 10000000, 500000))
    for i in x:
        time1 = time.time()
        s = adder(i)
        time2 = time.time()
        s = jit_adder(i)
        time3 = time.time()
        time_adder.append(time2 - time1)
        time_jit_adder.append(time3 - time2)

    fig, ax1 = plt.subplots()
    color = 'black'
    ax1.set_xlabel('Numbers')
    ax1.set_ylabel('Time (s)', color=color)
    ax1.plot(x[1:], time_adder[1:], color=color, label='python')
    ax1.tick_params(axis='y', labelcolor=color)

    ax2 = ax1.twinx()
    color = 'red'
    ax2.set_ylabel('Time (s)', color=color)
    ax2.plot(x[1:], time_jit_adder[1:], color=color, label='jit')
    ax2.tick_params(axis='y', labelcolor=color)
    plt.title('Running time difference via using jit')

    fig.tight_layout()
    plt.legend()
    plt.savefig('jit.png')

最终得到的时间对比图结果如下所示：



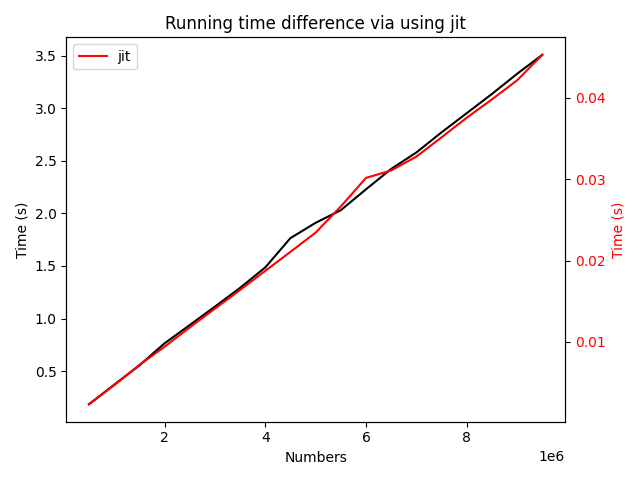
需要提醒的是，黑色的曲线所对应的坐标轴是左边黑色标识的坐标轴，而红色的曲线所对应的坐标轴是右边红色标识的坐标轴。因此，这个图给我们的提示信息是，使用即时编译技术之后，加速的倍率大约为\(10^2\)。这个加速倍率相对来说更加可以接受，因为C++等语言比python直接计算的速度在特定场景下大概就是要快上几百倍。

用numba.vectorize执行向量化计算

关于向量化计算的原理和方法，在这篇文章中有比较好的描述，这里放上部分截图说明：





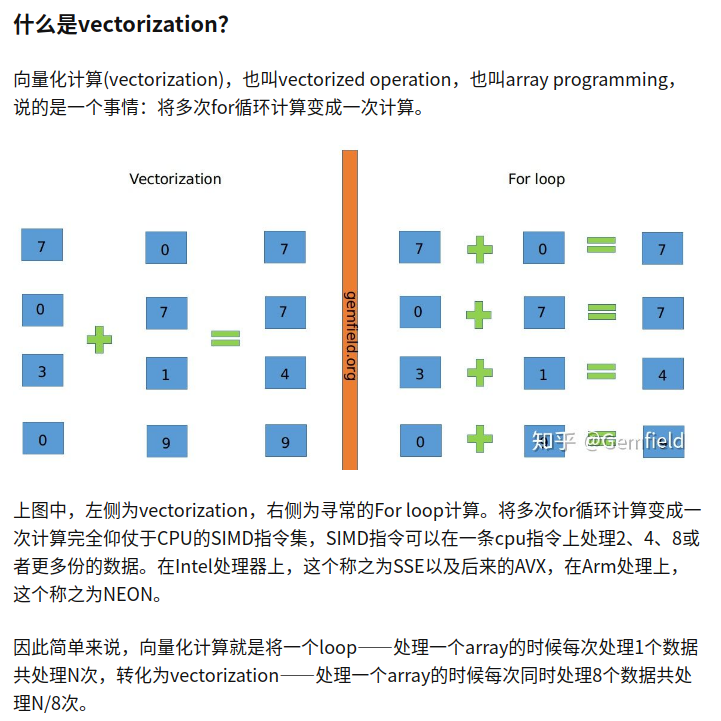
总结为，向量化计算的方法本质上也是一种并行化计算的方法，并行化技术的可行性是来源于SIMD技术，在指令集的层面对数据进行并行化的处理。在numpy的库中是自带支持SIMD的向量化计算的，因此速度非常的高，比如numpy.dot函数就是通过向量化计算来实现的。但是numpy能够执行的任务仅仅局限在numpy自身所支持的有限的函数上，因此如果是需要一个不同的函数，那么就需要用到numba的向量化计算模块了。

# test_vectorize.py

from numba import vectorize
import numpy as np
import time
import matplotlib.pyplot as plt

def ddot(max):
    s = 0
    np.random.seed(1)
    a1 = np.random.randn(max)
    np.random.seed(2)
    a2 = np.random.randn(max)
    for i in range(max):
        s += a1[i] * a2[i]
    return s

@vectorize
def jit_ddot(max):
    s = 0
    np.random.seed(1)
    a1 = np.random.randn(max)
    np.random.seed(2)
    a2 = np.random.randn(max)
    for i in range(max):
        s += a1[i] * a2[i]
    return s

def numpy_ddot(max):
    np.random.seed(1)
    a1 = np.random.randn(max)
    np.random.seed(2)
    a2 = np.random.randn(max)
    return np.dot(a1, a2)

if __name__ == '__main__':
    time_ddot = []
    time_jit_ddot = []
    time_numpy_ddot = []
    x = list(range(1, 1000000, 50000))
    for i in x:
        time1 = time.time()
        s = ddot(i)
        time2 = time.time()
        s = jit_ddot(i)
        time3 = time.time()
        s = numpy_ddot(i)
        time4 = time.time()
        time_ddot.append(time2 - time1)
        time_jit_ddot.append(time3 - time2)
        time_numpy_ddot.append(time4 - time3)

    fig, ax1 = plt.subplots()
    color = 'black'
    ax1.set_xlabel('Numbers')
    ax1.set_ylabel('Time (s)', color=color)
    ax1.plot(x[1:], time_ddot[1:], color=color, label='python')
    ax1.tick_params(axis='y', labelcolor=color)

    ax2 = ax1.twinx()
    color = 'red'
    ax2.set_ylabel('Time (s)', color=color)
    ax2.plot(x[1:], time_jit_ddot[1:], color=color, label='jit')
    ax2.plot(x[1:], time_numpy_ddot[1:], 's', color=color, label='numpy')
    ax2.tick_params(axis='y', labelcolor=color)
    plt.title('Running time difference via using jit')

    fig.tight_layout()
    plt.legend()
    plt.savefig('jit.png')

运行结果如下：



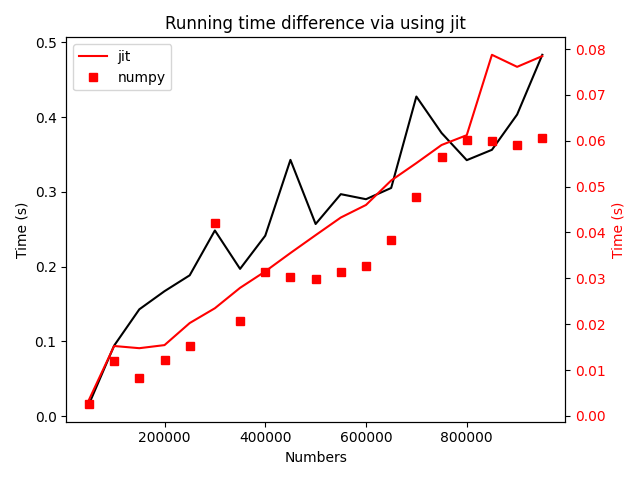
可以看到虽然相比与numpy的同样的向量化计算方法，numba速度略慢一些，但是都比纯粹的python代码性能要高两个量级。这里也给我们一个启发，如果追求极致的性能，最好是尽可能的使用numpy中已有的函数。当然，在一些数学函数的计算上，numpy的速度比math还是要慢上一些的，这里我们就不展开介绍了。

总结概要

本文介绍了numba的两个装饰器的原理与测试案例，以及python中两坐标轴绘图的案例。其中基于即时编译技术jit的装饰器，能够对代码中的for循环产生较大的编译优化，可以配合并行技术使用。而基于SIMD的向量化计算技术，也能够在向量的计算中，如向量间的乘加运算等场景中，实现巨大的加速效果。这都是非常底层的优化技术，但是要分场景使用，numba这个强力的工具并不能保证在所有的计算场景下都能够产生如此的加速效果。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/numba.html

作者ID：DechinPhy

更多原著文章请参考：https://www.cnblogs.com/dechinphy/

参考链接

1. https://zhuanlan.zhihu.com/p/78882641
2. https://blog.csdn.net/yuanzhoulvpi/article/details/105307338
3. https://zhuanlan.zhihu.com/p/68805601
4. https://zhuanlan.zhihu.com/p/193035135
5. https://zhuanlan.zhihu.com/p/72953129