Cooley-Tukey算法 （蝶形算法）

Cooley－Tukey算法差别于其它FFT算法的一个重要事实就是N的因子能够随意选取。这样也就能够使用N＝r^S的Radix－r算法了。最流行的算法都是以r＝2或r＝4为基的，最简单的DFT不须要不论什么乘法就能够实现。比如：在S级且r＝2的情形下，下列索引映射的结果是：

　　S＞2时的－个一般惯例是，在信号流程图中2点DFT是以蝶形图的形式绘出的，图1给出了8点变换的图示。信号流程图己经简化成用全部指向一个节点的箭头都代表加法的形式了，而常系数乘法则是在箭头上加一个因子表示。Radix－r算法具有log_r（N）级，而且每组都有同样类型的旋转因子。

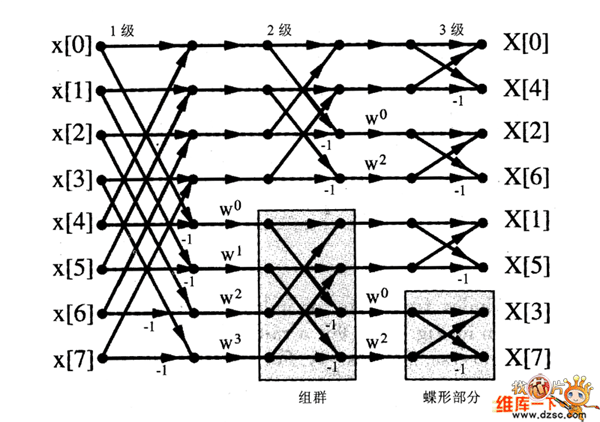
　　图1 radix－2的长度为8的频率抽取算法

　　从图的信号流程图能够看出，计算能够“就地”完毕，也就是蝶形所使用的存储位置能够被重写，由于数据在下一步的计算中已不再须要了。Radix－2变换的旋转因子乘法总数是：

由于每两个箭头仅有一个旋转因子。

　　因为图1中的算法在频域中開始将最初的DFT分成更短的DFT，所以这样的算法就叫作频率抽取（decimatiON－in－frequency，DIF）算法。典型的输入值是按顺序出现的，而频率值的索引是按位逆序的。表给出了DIF Radix－2算法的特征值。

　　表 频率抽取的Radix－2 FFT

　　我们还能够用时间抽取（decimation h time，DIT）构造一种算法。在该情况下，首先将输入序列分开，就会发现全部频率值都是按顺序出现的。

　　图2给出了索引41的radix－2和radix－4算法的必要索引变换。radix－2算法须要位顺序的反转，也就是位逆序。而radix－4须要首先构造一个2位的“数字”然后再反转这些数字，这样的操作就称为数字逆序。

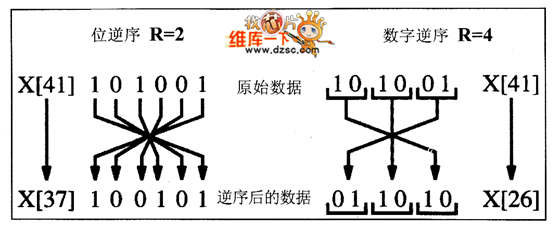
　　图2 位逆序和数字逆序