ZOJ 3216 Compositions (矩阵快速幂)

题意：求把 n 拆成几个大于等于 k 的数的和的方案数。

析：根据题目很容易写出递推式，f[i] = f[i-1] + f[i-k]，什么意思呢，f[i-1] 表示是进行加 1 操作，那么可以给 n-1 中拆分的任何一个数加1，还有一个就是再加一个数，那么就是 f[i-k]。然后进行构造矩阵。

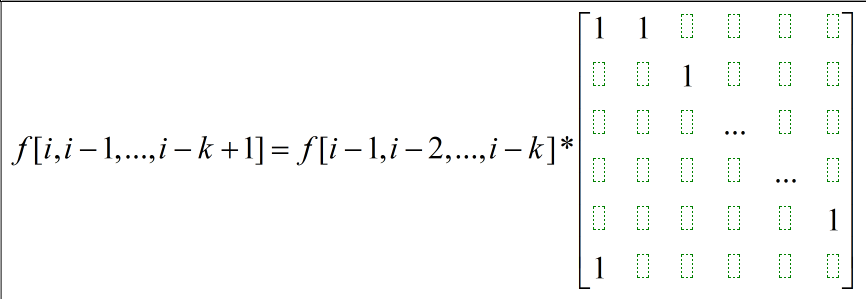
代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define be begin()
#define ed end()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,n,x)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.in", "r", stdin)
#define freopenw freopen("out.out", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-6;
const int maxn = 100 + 10;
const int maxm = 1e6 + 10;
const LL mod = 1000000007;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}
inline int readInt(){ int x;  scanf("%d", &x);  return x; }

struct Matrix{
  LL a[30][30];
  int n;
  void init(){ ms(a, 0); }
  void normal(){ FOR(i, n, 0)  a[i][i] = 1; }
  Matrix operator * (const Matrix &rhs){
    Matrix res; res.init();  res.n = n;
    FOR(i, n, 0)  FOR(j, n, 0)  FOR(k, n, 0)
      res.a[i][j] = (res.a[i][j] + a[i][k] * rhs.a[k][j]) % mod;
    return res;
  }
};

Matrix fast_pow(Matrix a, int n){
  Matrix res; res.n = a.n;  res.init();  res.normal();
  while(n){
    if(n&1)  res = res * a;
    a = a * a;
    n >>= 1;
  }
  return res;
}

LL fast_pow(LL a, int n){
  LL res = 1;
  while(n){
    if(n&1)  res = res * a % mod;
    a = a * a % mod;
    n >>= 1;
  }
  return res;
}

int main(){
  int T;  cin >> T;
  while(T--){
    scanf("%d %d", &n, &m);
    if(n < m){ puts("0");  continue; }
    else if(n < m + m){ puts("1");  continue; }
    else if(m == 1){ printf("%lld\n", fast_pow(2LL, n-1));  continue; }
    Matrix x, y;  x.init();  y.init();  x.n = y.n = m;
    for(int i = 0; i < m; ++i)  y.a[0][i] = 1;
    x.a[0][0] = x.a[m-1][0] = 1;
    for(int i = 1; i < m; ++i)  x.a[i-1][i] = 1;
    x = y * fast_pow(x, n - m - m + 1);
    printf("%lld\n", x.a[0][0]);
  }
  return 0;
}