【Luogu】P2764最小路径覆盖（拆点求最大匹配）

　　题目链接

　　这个……学了一条定理

　　最小路径覆盖=原图总点数-对应二分图最大匹配数

　　这个对应二分图……是什么呢？

　　就是这样

　　

　　这是原图

　　

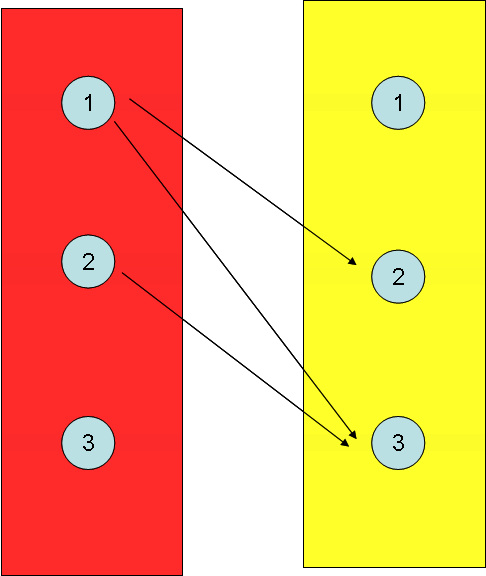
　　这是拆点之后对应的二分图。

　　

　　然后咱们的目标就是从这张图上跑出个最大流来，然后用原图的总点数减去就是答案。

　　至于记录路径……我发现有一个规律是可以在Dinic跑DFS的时候记。

　　别的我不知道了。因为我只会Dinic。

　　代码如下。

　　

#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
#include<queue>
#include<cstdlib>
#define maxn 3000
#define maxm 60000
using namespace std;
inline long long read(){
    long long num=,f=;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')    f=-;
        ch=getchar();
    }
    while(isdigit(ch)){
        num=num*+ch-'';
        ch=getchar();
    }
    return num*f;
}

inline int count(int i){    return i&?i+:i-;    }

struct Edge{
    int next,to,val;
}edge[maxm*];
int head[maxn*],num;
inline void addedge(int from,int to,int val){
    edge[++num]=(Edge){head[from],to,val};
    head[from]=num;
}
inline void add(int from,int to,int val){
    addedge(from,to,val);
    addedge(to,from,);
}

bool vis[maxn];
int dfn[maxn];
int list[maxn*];
int Start,End;
int road[maxn*];
int n,m;
bool flag;

bool bfs(){
    memset(vis,,sizeof(vis));
    queue<int> q; dfn[Start]=; vis[Start]=;    q.push(Start);
    while(!q.empty()){
        int from=q.front();    q.pop();
        for(int i=head[from];i;i=edge[i].next){
            int to=edge[i].to;
            if(vis[to]||edge[i].val<=)    continue;
            vis[to]=;
            dfn[to]=dfn[from]+;
            q.push(to);
        }
    }
    return vis[End];
}

int dfs(int x,int val){
    //printf("%d %d\n",x,val);
    if(val==||x==End)    return val;
    vis[x]=;    int flow=;
    for(int &i=list[x];i;i=edge[i].next){
        int to=edge[i].to;
        if(vis[to]||dfn[to]!=dfn[x]+||edge[i].val<=)    continue;
        int now=dfs(to,min(val,edge[i].val));
        val-=now;    edge[i].val-=now;    flow+=now;    edge[count(i)].val+=now;
        if(val<=){
            road[x]=to;
            break;
        }
    }
    if(flow!=val)    dfn[x]=-;
    return flow;
}

int maxflow(){
    int ans=;
    while(bfs()){
        memset(vis,,sizeof(vis));
        for(int i=Start;i<=End;++i)    list[i]=head[i];
        int now=dfs(Start,0x7fffffff);
        if(!now)    break;
        ans+=now;
    }
    return ans;
}

int main(){
    n=read(),m=read();End=n*+;
    for(int i=;i<=n;++i){
        add(Start,i,);
        add(i+n,End,);
    }
    for(int i=;i<=m;++i){
        int from=read(),to=read();
        add(from,to+n,);
    }
    int ans=maxflow();
    memset(vis,,sizeof(vis));
    for(int i=;i<=n;++i){
        if(road[i]==)    continue;
        int now=i;
        while(now!=End&&now){
            printf("%d ",now>n?now-=n:now);
            int x=road[now];    road[now]=;
            now=x;
        }
        printf("\n");
    }
    printf("%d",n-ans);
    return ;
}