NOI 2012 魔幻棋盘 | 二维差分 + 二维线段树

题目：luogu 2086

二维线段树，按套路差分原矩阵，gcd( x₁, x₂, ……, x_n ) = gcd( x_i, x₂ - x₁, ……, x_n - x_n-1 )，必须要有一个原数 x_i，恰好每次询问都包含一个固定点 ( X , Y )，差分以它为中心就可以保证它是原值。以 e 为中心的二维差分如图。

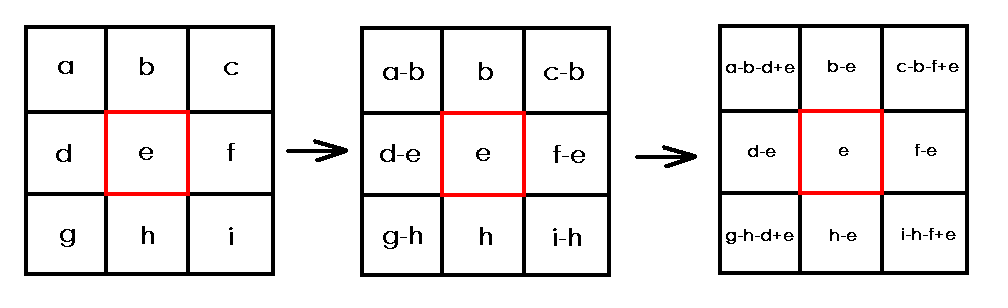
对于一维序列，修改区间 [ l , r ] 只需修改差分后的 l 和 r + 1 两点。那么对于二维，差分后的修改如下所示：

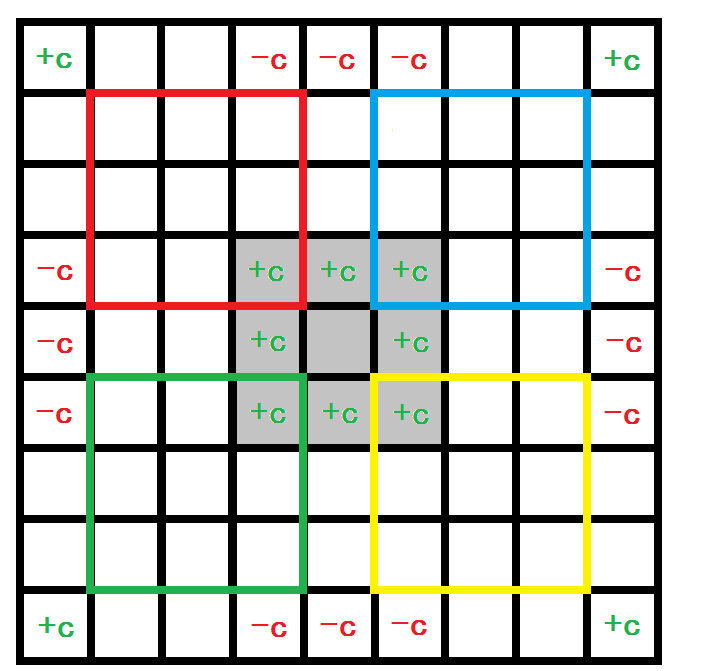
中间的灰色格子为守卫者所在地（为方便表示多个区域把它拆成了 9 格），以它为差分中心，若修改矩阵在它的右下方，即黄色区域，设它的左上角坐标为 ( x1, y1)，右下角坐标 ( x2, y2 )，则需在 ( x1, y1 ) 处 + c，( x1, y2+1 ) 处 - c，( x2+1, y1 ) 处 - c，( x2 + 1, y2 + 1) 处 +c。

其他区域同理。再加上守卫者正上方、正下方、正左方、正右方的区域，一共 8 种情况。如果一个修改矩阵包含多个区域，就将其划分为若干个子矩阵处理。

这样就将巨慢的区间修改转换成了单点修改，每修改完一个点，pushup( ) 维护 gcd 即可。

另外读入的时候，500000 * 500000 的二维数组是开不了的，需要动态分配内存；或者开一个 500000 的一维数组读入，判断每一行的末端在哪里。

讨论的时候有些麻烦，下面列一下大致的情况：（黄色表示修改的区域，绿色加，红色减）

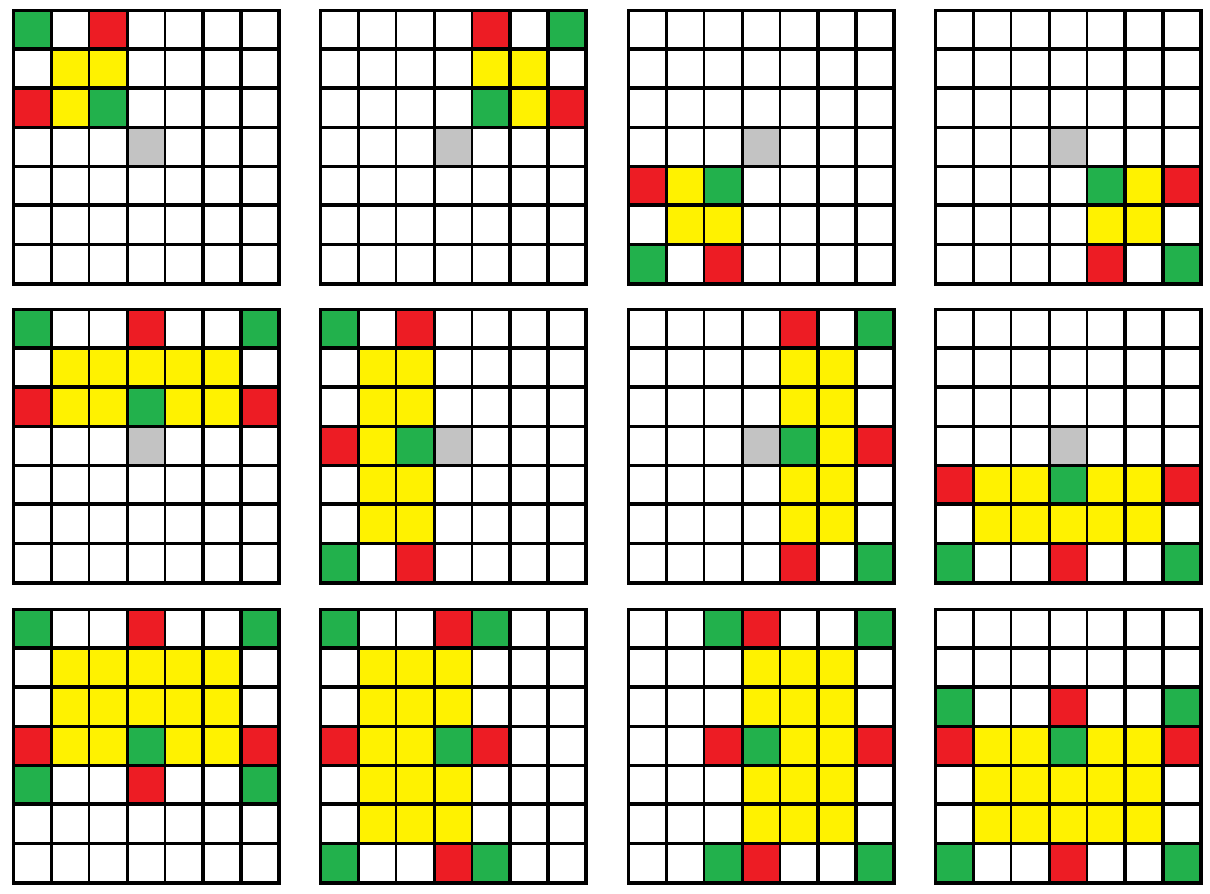
仔细观察后，发现可分为三种情况：① 包含守卫者 ( X , Y )；② 包含 X 行或 Y 列；③ 只包含左上或左下、右上或右下区域。

细节诸多：

差分的时候不能用原数组减，因为前面的值会变，需要另开一个数组保存；

返回 gcd 的时候要取绝对值；二维线段树内层空间要开大。

 #include <cstdio>

 #include <string>

 const int N = ;

 typedef long long ll;

 int n, m; ll a[N], b[N];

 ll read() {

     ll x = , f = ;

     char c = getchar();

     while (!isdigit(c)) {

         if (c == '-') f = -;

         c = getchar();

     }

     while (isdigit(c)) {

         x = (x << ) + (x << ) + (c ^ );

         c = getchar();

     }

     return x * f;

 }

 ll abs(ll x) {

     if (x >= ) return x; return -x;

 }

 ll gcd(ll x, ll y) {

     if (y) return gcd(y, x % y); return abs(x);

 }

 struct inNode {

     ll val;

     inNode *ls, *rs;

     inNode() : val(), ls(NULL), rs(NULL) {}

 } inPool[N << ];

 inNode *newInNode () {

     static int cnt = ;

     return &inPool[++cnt];

 }

 void buildY(inNode *&cur, int l, int r, int x) {

     if (!cur) cur = newInNode();

     if (l == r) cur->val = a[(x - ) * m + l];

     else {

         int mid = l + ((r - l) >> );

         buildY(cur->ls, l, mid, x);

         buildY(cur->rs, mid + , r, x);

         cur->val = gcd(cur->ls->val, cur->rs->val);

     }

 }

 void updateY(inNode *&cur, int l, int r, int y, ll val) {

     if (l == r) cur->val += val;

     else {

         int mid = l + ((r - l) >> );

         if (y <= mid) updateY(cur->ls, l, mid, y, val);

         else updateY(cur->rs, mid + , r, y, val);

         cur->val = gcd(cur->ls ? cur->ls->val : , cur->rs ? cur->rs->val : );

     }

 }

 ll queryY(inNode *&cur, int l, int r, int y1, int y2) {

     if (y1 <= l && r <= y2) return cur->val;

     int mid = l + ((r - l) >> ); ll res = ;

     if (y1 <= mid) res = gcd(res, queryY(cur->ls, l, mid, y1, y2));

     if (mid < y2) res = gcd(res, queryY(cur->rs, mid + , r, y1, y2));

     return res;

 }

 struct outNode {

     inNode *root;

     outNode *ls, *rs;

     outNode() : root(NULL), ls(NULL), rs(NULL) {}

 } outPool[N << ], *root;

 outNode *newOutNode() {

     static int cnt = ;

     return &outPool[++cnt];

 }

 void maintain(inNode *&cur, inNode *&lc, inNode *&rc, int l, int r) {

     if (!cur) cur = newInNode();

     if (l == r) cur->val = gcd(lc->val, rc->val);

     else {

         int mid = l + ((r - l) >> );

         maintain(cur->ls, lc->ls, rc->ls, l, mid);

         maintain(cur->rs, lc->rs, rc->rs, mid + , r);

         cur->val = gcd(cur->ls->val ,cur->rs->val);

     }

 }

 void buildX(outNode *&cur, int l, int r) {

     if (!cur) cur = newOutNode();

     if (l == r) buildY(cur->root, , m, l);

     else {

         int mid = l + ((r - l) >> );

         buildX(cur->ls, l, mid);

         buildX(cur->rs, mid + , r);

         maintain(cur->root, cur->ls->root, cur->rs->root, , m);

     }

 }

 void change(inNode *&cur, int l, int r, int y, ll val) {

     if (l == r) cur->val = val;

     else {

         int mid = l + ((r - l) >> );

         if (y <= mid) change(cur->ls, l, mid, y, val);

         else change(cur->rs, mid + , r, y, val);

         cur->val = gcd(cur->ls ? cur->ls->val : , cur->rs ? cur->rs->val : );

     }

 }

 void updateX(outNode *&cur, int l, int r, int x, int y, ll val) {

     if (x <=  || y <=  || x > n || y > m) return;

     if (l == r) updateY(cur->root, , m, y, val);

     else {

         int mid = l + ((r - l) >> ); ll lv = , rv = ;

         if (x <= mid) updateX(cur->ls, l, mid, x, y, val);

         else updateX(cur->rs, mid + , r, x, y, val);

         if (cur->ls) lv = queryY(cur->ls->root, , m, y, y);

         if (cur->rs) rv = queryY(cur->rs->root, , m, y, y);

         change(cur->root, , m, y, gcd(lv, rv));

     }

 }

 ll queryX(outNode *&cur, int l, int r, int x1, int x2, int y1, int y2) {

     if (x1 <= l && r <= x2) return queryY(cur->root, , m, y1, y2);

     int mid = l + ((r - l) >> ); ll res = ;

     if (x1 <= mid) res = gcd(res, queryX(cur->ls, l, mid, x1, x2, y1, y2));

     if (mid < x2) res = gcd(res, queryX(cur->rs, mid + , r, x1, x2, y1, y2));

     return res;

 }

 int main() {

     n = read(), m = read();    int X = read(), Y = read(), T = read();

     for (int i = ; i <= n * m; ++ i) a[i] = read();

     for (int i = ; i <= n * m; ++ i) {

         if ((i - ) % m +  < Y) b[i] = a[i] - a[i + ];

         else if ((i - ) % m +  > Y) b[i] = a[i] - a[i - ];

         else b[i] = a[i];

     }

     for (int i = ; i <= n * m; ++ i) {

         if ((i - ) / m +  < X) a[i] = b[i] - b[i + m];

         else if ((i - ) / m +  > X) a[i] = b[i] - b[i - m];

         else a[i] = b[i];

     }

     buildX(root, , n);

     while (T--) {

         int opt = read(), x1 = read(), y1 = read(), x2 = read(), y2 = read();

         if (opt == ) {

             x1 = X - x1, x2 = X + x2, y1 = Y - y1, y2 = Y + y2;

             printf("%lld\n", queryX(root, , n, x1, x2, y1, y2));

         } else {

             ll val = read();

             if (x1 <= X && x2 >= X && y1 <= Y && y2 >= Y) {    //包含(X,Y)

                 updateX(root, , n, X, Y, val);

                 updateX(root, , n, x1 - , y1 - , val);

                 updateX(root, , n, x1 - , y2 + , val);

                 updateX(root, , n, x2 + , y1 - , val);

                 updateX(root, , n, x2 + , y2 + , val);

                 updateX(root, , n, x1 - , Y, -val);

                 updateX(root, , n, x2 + , Y, -val);

                 updateX(root, , n, X, y1 - , -val);

                 updateX(root, , n, X, y2 + , -val);

             } else if (y1 <= Y && y2 >= Y) {                //包含Y列

                 if (x1 < X) {                                //在(X,Y)上方

                     updateX(root, , n, x2, Y, val);

                     updateX(root, , n, x1 - , y1 - , val);

                     updateX(root, , n, x1 - , y2 + , val);

                     updateX(root, , n, x1 - , Y, -val);

                     updateX(root, , n, x2, y1 - , -val);

                     updateX(root, , n, x2, y2 + , -val);

                 } else {                                    //在(X,Y)下方

                     updateX(root, , n, x1, Y, val);

                     updateX(root, , n, x2 + , y1 - , val);

                     updateX(root, , n, x2 + , y2 + , val);

                     updateX(root, , n, x2 + , Y, -val);

                     updateX(root, , n, x1, y1 - , -val);

                     updateX(root, , n, x1, y2 + , -val);

                 }

             } else if (x1 <= X && x2 >= X) {                //包含X行

                 if (y1 < Y) {                                //在(X,Y)左边

                     updateX(root, , n, X, y2, val);

                     updateX(root, , n, x1 - , y1 - , val);

                     updateX(root, , n, x2 + , y1 - , val);

                     updateX(root, , n, X, y1 - , -val);

                     updateX(root, , n, x1 - , y2, -val);

                     updateX(root, , n, x2 + , y2, -val);

                 } else {                                    //在(X,Y)右边

                     updateX(root, , n, X, y1, val);

                     updateX(root, , n, x1 - , y2 + , val);

                     updateX(root, , n, x2 + , y2 + , val);

                     updateX(root, , n, X, y2 + , -val);

                     updateX(root, , n, x1 - , y1, -val);

                     updateX(root, , n, x2 + , y1, -val);

                 }

             } else if (x1 < X && y1 < Y) {                    //左上区域

                 updateX(root, , n, x2, y2, val);

                 updateX(root, , n, x1 - , y1 - , val);

                 updateX(root, , n, x1 - , y2, -val);

                 updateX(root, , n, x2, y1 - , -val);

             } else if (x1 < X && y1 > Y) {                    //右上区域

                 updateX(root, , n, x2, y1, val);

                 updateX(root, , n, x1 - , y2 + , val);

                 updateX(root, , n, x1 - , y1, -val);

                 updateX(root, , n, x2, y2 + , -val);

             } else if (x1 > X && y1 < Y) {                    //左下区域

                 updateX(root, , n, x1, y2, val);

                 updateX(root, , n, x2 + , y1 - , val);

                 updateX(root, , n, x1, y1 - , -val);

                 updateX(root, , n, x2 + , y2, -val);

             } else {                                        //右下区域

                 updateX(root, , n, x1, y1, val);

                 updateX(root, , n, x2 + , y2 + , val);

                 updateX(root, , n, x1, y2 + , -val);

                 updateX(root, , n, x2 + , y1, -val);

             }

         }

     }

     return ;

 }

NOI 2012 魔幻棋盘 | 二维差分 + 二维线段树的更多相关文章

【坐标变换】【二维偏序】【线段树】Gym - 100820G - Racing Gems
题意:第一象限有n个点,你从x正半轴任选一个位置出发,vy恒定,vx可以任意变化,不过只能在-vy/r到vy/r之间变化,问你最多能经过多少个点. 暴力dp是n^2,不可取. 注意到,一个点,所能到达 ...
[BZOJ3196] 二逼平衡树 [权值线段树套位置平衡树]
题面洛咕题面思路没错我就是要不走寻常路! 看看那些外层位置数据结构,必须二分的,$O(n\log^3 n)$的做法吧! 看看那些cdq分治/树状数组套线段树的,空间$O(n\log^2 n)$挤 ...
二叉搜索树TREE（线段树，区间DP）
前言线段树+区间DP题,线段树却不是优化DP的,是不是很意外? 题面二叉搜索树是一种二叉树,每个节点都有一个权值,并且一个点的权值比其左子树里的点权值都大,比起右子树里的点权值都小. 一种朴素的向 ...
[BZOJ3307]:雨天的尾巴（LCA+树上差分+权值线段树）
题目传送门题目描述: N个点,形成一个树状结构.有M次发放,每次选择两个点x,y对于x到y的路径上(含x,y)每个点发一袋Z类型的物品.完成所有发放后,每个点存放最多的是哪种物品. 输入格式: 第一 ...
洛谷1083（差分+二分 or 线段树）
第一种方法:可以二分最大天数订单的答案然后通过差分求一下是否可行. ; int n, m, a[maxn], ans; struct section { int cnt, l, r; }b[maxn] ...
2019杭电多校6 hdu6638 Snowy Smile（二维最大矩阵和线段树）
http://acm.hdu.edu.cn/showproblem.php?pid=6638 题意:给你一些点的权值,让找一个矩形圈住一部分点,问圈住点的最大权值和分析:由于是稀疏图,明显要先把x, ...
刷题总结——二逼平衡树（bzoj3224线段树套splay）
题目: Description 您需要写一种数据结构(可参考题目标题),来维护一个有序数列,其中需要提供以下操作:1.查询k在区间内的排名2.查询区间内排名为k的值3.修改某一位值上的数值4.查询k在 ...
2018HDU多校二 -F 题 Naive Operations(线段树)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6315 In a galaxy far, far away, there are two integer ...
NOIp 2012 #2 借教室 Label：区间修改线段树
题目描述在大学期间,经常需要租借教室.大到院系举办活动,小到学习小组自习讨论,都需要向学校申请借教室.教室的大小功能不同,借教室人的身份不同,借教室的手续也不一样. 面对海量租借教室的信息,我们自然 ...

随机推荐

FreeBSD 8
FreeBSD 8.0的安装过程和7.2区别不大.先在FreeBSD官方网站上下载安装镜像,我一般都下载DVD的ISO,也有人爱好下最小的安装包,然后通过FTP或HTTP方式从网上下载各个程序包. 这 ...
ffmpeg一些filter使用方法、以及一些功能命令
1.加字幕命令:ffmpeg -i <input> -filter_complex subtitles=filename=<SubtitleName>-y <outpu ...
更改已经签名的app中的内容
转载请说明出处http://blog.csdn.net/andywuchuanlong 记得上次在南昌中兴的一个项目中遇到过一个这种需求:一个app能够给多个渠道商去运营,渠道商推广出去能够获得对应的 ...
Cocos2d-x 3.1.1 学习日志5--cocos2d-x3.1.1打飞机的实现
近期学习了cocos2dx3.1.1的一些功能,认为和曾经版本号改的太多了. 所以就做了一个小项目--打飞机来练习练习,在这里我仅仅讲飞机实现的步骤,至于代码.回复5次就可以获得coco2d-x3.1 ...
CSS3中的动画效果-------Day72
还记得么,在前面也曾实现过"仅仅用css让div动起来",还记得当时是怎么实现的么,是的,transition,针对的也比較局限,仅仅有旋转角度啊,长宽啊之类的,所以说,与其说是动 ...
ARM architecture
http://en.wikipedia.org/wiki/ARM_architecture ARM architecture ARM architectures The ARM logo De ...
smali语法（一）
一.什么是Smali? Smali,Baksmali分别是指安卓系统里的Java虚拟机(Dalvik)所使用的一种dex格式文件的汇编器,反汇编器.其语法是一种宽松式的Jasmin/dedexer语法 ...
Spring Boot实现STOMP协议的WebSocket
关注公众号:锅外的大佬每日推送国外优秀的技术翻译文章,励志帮助国内的开发者更好地成长! WebSocket协议是应用程序处理实时消息的方法之一.最常见的替代方案是长轮询(long polling)和 ...
Centos7-安装Apache2.4+PHP5.6
linux系统CentOS7先下载Apache需要依赖的软件1.APR下载地址http://apr.apache.org/download.cgiwget下载路径http://mirror.bit.e ...
cURL实现Get和Post
1.Get请求: //初始化 $ch = curl_init(); //设置选项,包括URL curl_setopt($ch, CURLOPT_URL, "http://www.jb51.n ...

NOI 2012 魔幻棋盘 | 二维差分 + 二维线段树

NOI 2012 魔幻棋盘 | 二维差分 + 二维线段树的更多相关文章

随机推荐

热门专题