思维水题：UVa512-Spreadsheet Tracking

Spreadsheet Tracking

Data in spreadsheets are stored in cells, which are organized in rows (r) and columns (c). Some operations on spreadsheets can be applied to single cells (r,c), while others can be applied to entire rows or columns. Typical cell operations include inserting and deleting rows or columns and exchanging cell contents.

Some spreadsheets allow users to mark collections of rows or columns for deletion, so the entire collection can be deleted at once. Some (unusual) spreadsheets allow users to mark collections of rows or columns for insertions too. Issuing an insertion command results in new rows or columns being inserted before each of the marked rows or columns. Suppose, for example, the user marks rows 1 and 5 of the spreadsheet on the left for deletion. The spreadsheet then shrinks to the one on the right.



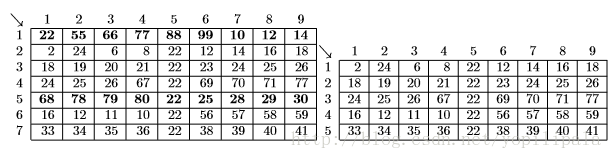
If the user subsequently marks columns 3, 6, 7, and 9 for deletion, the spreadsheet shrinks to this.



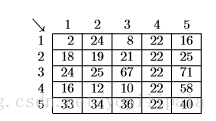
If the user marks rows 2, 3 and 5 for insertion, the spreadsheet grows to the one on the left. If the user then marks column 3 for insertion, the spreadsheet grows to the one in the middle. Finally, if the user exchanges the contents of cell (1,2) and cell (6,5), the spreadsheet looks like the one on the right.



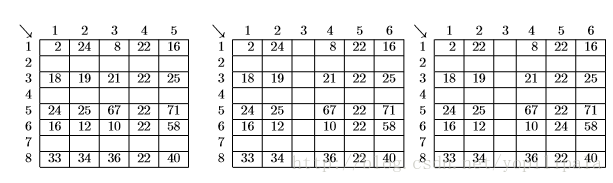
You must write tracking software that determines the final location of data in spreadsheets that result from row, column, and exchange operations similar to the ones illustrated here.

Input

The input consists of a sequence of spreadsheets, operations on those spreadsheets, and queries about them. Each spreadsheet definition begins with a pair of integers specifying its initial number of rows (r) and columns (c), followed by an integer specifying the number (n) of spreadsheet operations. Row and column labeling begins with 1. The maximum number of rows or columns of each spreadsheet is limited to 50. The following n lines specify the desired operations.

An operation to exchange the contents of cell (r1,c1) with the contents of cell (r2,c2) is given by: EX r1 c1 r2 c2

The four insert and delete commands—DC (delete columns), DR (delete rows), IC (insert columns), and IR (insert rows) are given by:

< command > A x1 x2 … xA where < command > is one of the four commands; A is a positive integer less than 10, and x1,…,xA are the labels of the columns or rows to be deleted or inserted before. For each insert and delete command, the order of the rows or columns in the command has no significance. Within a single delete or insert command, labels will be unique.

The operations are followed by an integer which is the number of queries for the spreadsheet. Each query consists of positive integers r and c, representing the row and column number of a cell in the original spreadsheet. For each query, your program must determine the current location of the data that was originally in cell (r,c). The end of input is indicated by a row consisting of a pair of zeros for the spreadsheet dimensions.

Output

For each spreadsheet, your program must output its sequence number (starting at 1). For each query, your program must output the original cell location followed by the final location of the data or the word ‘GONE’ if the contents of the original cell location were destroyed as a result of the operations. Separate output from different spreadsheets with a blank line.

The data file will not contain a sequence of commands that will cause the spreadsheet to exceed the maximum size.

Sample Input

7

9 5

DR 2 1 5

DC 4 3 6 7 9

IC 1 3 IR 2 2 4

EX 1 2 6 5

4

4 8

5 5

7 8

6 5

0 0

Sample Output

Spreadsheet #1

Cell data in (4,8) moved to (4,6)

Cell data in (5,5) GONE

Cell data in (7,8) moved to (7,6)

Cell data in (6,5) moved to (1,2)

---

解题心得：

1. 题意就是给你一个表，然后进行行列的删除、增加空白的行列、两个个表格的交换操作，然后询问原本表中的位置的值在进行一系列操作之后在表中的位置（或者不存在）。
2. 这个题思维难度不是很大，但是它要折磨你，很恼火，稍不注意就会写bug，做的方法有很多，我这里用的是简单的模拟。要注意一点就是这个题目上面给的例子并不是样例，只是给你解释一下大概的意思，被坑。
3. 如果就模拟，可以建立两个表，一个初始表，一个变化后的表，然后直接对照这两个表就行了，但是在模拟的过程中要注意，每次插入或者删除操作是同时进行的（就是不能在前面的删除操作过程中对下面要进行的行列的操作产生影响），所有在插入或者删除的时候要先从从数值大的行列进行操作，不然先改变前面的行或者列会影响后面的行和列。
4. 然后就是输出问题要注意其中一句话，将每两个例子用空白行分离，但最后一个例子后面不打印空行，不注意会PE。

---

#include<bits/stdc++.h>
using namespace std;
const int maxn = 60;
int maps[2][maxn][maxn];//maps[0][n][m]表示原表，maps[1][n][m]表示改变后表
int op[maxn];
int n,m,q,n1,m1;
char s[maxn];

void EX()
{
    int r1,c1,c2,r2;
    scanf("%d%d%d%d",&r1,&c1,&r2,&c2);
    swap(maps[1][r1][c1],maps[1][r2][c2]);
}

void pre_maps()
{
    int t = 1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            maps[0][i][j] = maps[1][i][j] = t++;
}

void DR()
{
    int times;
    scanf("%d",&times);
    for(int i=0;i<times;i++)
        scanf("%d",&op[i]);
    sort(op,op+times);//先对后面的行列进行操作以免产生影响，后面的后面
    for(int i=times-1;i>=0;i--)
    {
        int r = op[i];
        for(int i=r;i<=n1;i++)
            for(int j=1;j<=m1;j++)
                maps[1][i][j] = maps[1][i+1][j];
    }
    n1-=times;//记录剩下的行列
}

void DC()
{
    int times;
    scanf("%d",&times);
    for(int i=0;i<times;i++)
        scanf("%d",&op[i]);
    sort(op,op+times);
    for(int i=times-1;i>=0;i--)
    {
        int c = op[i];
        for(int i=c;i<=m1;i++)
            for(int j=1;j<=n1;j++)
                maps[1][j][i] = maps[1][j][i+1];
    }
    m1-=times;
}

void IR()
{
    int times;
    scanf("%d",&times);
    for(int i=0;i<times;i++)
        scanf("%d",&op[i]);
    sort(op,op+times);
    for(int i=times-1;i>=0;i--)
    {
        int r = op[i];
        for(int i=n1+1;i>r;i--)
            for(int j=1;j<=m1;j++)
                maps[1][i][j] = maps[1][i-1][j];
        for(int j=1;j<=m1;j++)
            maps[1][r][j] = 0;
        n1++;
    }
}

void IC()
{
    int times;
    scanf("%d",&times);
    for(int i=0;i<times;i++)
        scanf("%d",&op[i]);
    sort(op,op+times);
    for(int i=times-1;i>=0;i--)
    {
        int c = op[i];
        for(int i=m1+1;i>c;i--)
            for(int j=1;j<=n1;j++)
                maps[1][j][i] = maps[1][j][i-1];
        for(int i=1;i<=n1;i++)
            maps[1][i][c] = 0;
        m1++;
    }
}

void _find(int r,int c)
{
    int va = maps[0][r][c];
    for(int i=1;i<=n1;i++)
        for(int j=1;j<=m1;j++)
        {
            if(maps[1][i][j] == va)
            {
                printf("Cell data in (%d,%d) moved to (%d,%d)\n",r,c,i,j);
                return;
            }
        }
    printf("Cell data in (%d,%d) GONE\n",r,c);
}

int main()
{
    int Case = 1;
    bool flag = false;
    while(scanf("%d%d",&n,&m))
    {
        if(n + m == 0)
            break;
        if(flag)
            printf("\n");//用来输出空行
        flag = true;
        n1 = n,m1 = m;
        memset(maps,0,sizeof(maps));
        pre_maps();
        int opr;
        scanf("%d",&opr);
        while(opr--)
        {
            scanf("%s",s);
            if(s[0] == 'E')
                EX();
            else if(s[0] == 'D' && s[1] == 'R')
                DR();
            else if(s[0] == 'D' && s[1] == 'C')
                DC();
            else if(s[0] == 'I' && s[1] == 'R')
                IR();
            else if(s[0] == 'I' && s[1] == 'C')
                IC();
        }
        int query;
        scanf("%d",&query);
        printf("Spreadsheet #%d\n",Case++);
        while(query--)
        {
            int r,c;
            scanf("%d%d",&r,&c);
            _find(r,c);
        }
    }
    return 0;
}