一张图展示：用两个栈来实现一个队列，完成队列的Push和Pop操作

一  基本思路

将s1作为存储空间，以s2作为临时缓冲区。
 
入队时，将元素压入s1。
 
出队时，将s1的元素逐个“倒入”（弹出并压入）s2，将s2的顶元素弹出作为出队元素，之后再将s2剩下的元素逐个“倒回”s1。

二 图示

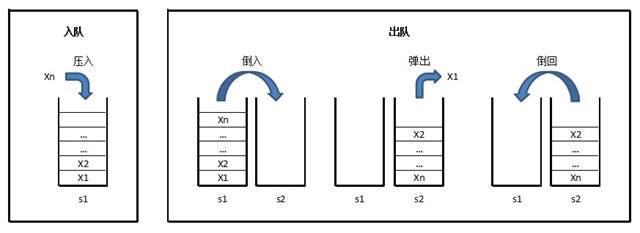
三 代码实现（Java）

import java.util.Stack;
 
public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
 
    public void push(int node) {
        stack1.push(node);
    }
 
    public int pop() {
        while(!stack1.isEmpty()){
            stack2.push(stack1.pop());
        }
        int first=stack2.pop();
        while(!stack2.isEmpty()){
            stack1.push(stack2.pop());
        }
        return first;
    }
}

四  优化

入队时，将元素压入s1。
出队时，判断s2是否为空，如不为空，则直接弹出顶元素；如为空，则将s1的元素逐个“倒入”s2，把最后一个元素弹出并出队。