POJ - 2135最小费用流

题目链接：http://poj.org/problem?id=2135

今天学习最小费用流。模板手敲了一遍。

产生了一个新的问题：对于一条无向边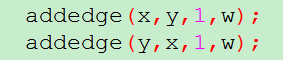，这样修改了正向边容量后，反向边不用管吗？

后来想了想，得出了个结论。路径所选的边只会包括正反中的一条。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
const int maxn = 2e3;
const int INF = 1e9;
int dist[maxn];
int pv[maxn],pe[maxn];
struct edge
{
    int to, cap, rev;
    int cost;
    edge(int a, int b, int c, int d)
    {
        to = a, cap = b, cost = c, rev = d;
    }
};
vector<edge> g[maxn];
void addedge(int from,int to,int cap,int cost)
{
    g[from].push_back(edge(to,cap,cost,g[to].size()));
    g[to].push_back(edge(from,,-cost,g[from].size()-));
}
int n;
int vis[maxn];
void SPFA(int s, int t)
{
    for(int i = ; i < maxn; i++) dist[i] = INF;
    memset(vis, , sizeof(vis));
    dist[s] = , vis[s] = ;
    queue<int> q;
    q.push(s);
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        vis[u] = ;
        for(int i = ; i < g[u].size(); i++)
        {
            edge &e = g[u][i];
            if(e.cap >  && (dist[e.to] - (dist[u] + e.cost)) > )
            {
                pv[e.to] = u, pe[e.to] = i;
                dist[e.to] = dist[u] + e.cost;
                if(!vis[e.to])
                {
                    vis[e.to] = ;
                    q.push(e.to);
                }
            }
        }
    }
}
int min_cost_flow(int s,int t,int f,int& max_flow)
{
    int ret = 0.0;
    while(f>)
    {
        SPFA(s, t);
        if(dist[t] == INF) return ret;///同一目的地，每次增广路都是最小费用
        ///当所有边的流量都流净后，即没有残余网络，返回。
        int d = f;
        for(int v=t;v!=s;v=pv[v])
        {
            d = min(d,g[pv[v]][pe[v]].cap);
        }
        f -= d;
        max_flow += d;
        ret += (int)d*dist[t]; ///走一单位就消耗dist[t]
        for(int v=t;v!=s;v=pv[v])
        {
            edge &e = g[pv[v]][pe[v]];
            e.cap -= d;
            g[v][e.rev].cap += d;
        }
    }
    return ret;
}
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    int s=,t=n+;
    addedge(s,,,);
    addedge(n,t,,);
    for(int i=;i<=m;i++)
    {
        int x,y,w;
        scanf("%d %d %d",&x,&y,&w);
        addedge(x,y,,w);
        addedge(y,x,,w);
    }
   // printf("%d\n",e[6].cap);
   ///反向边不用管它，因为路径只会选择正反里面的一条边
    int maxflow = ;
    int ans = min_cost_flow(s,t,INF,maxflow);
    for(int i = ; i < maxn; i++) g[i].clear();
    printf("%d\n",ans);
    return ;
}

Code