jmeter正则表达式token提取

例：

添加正则

配置

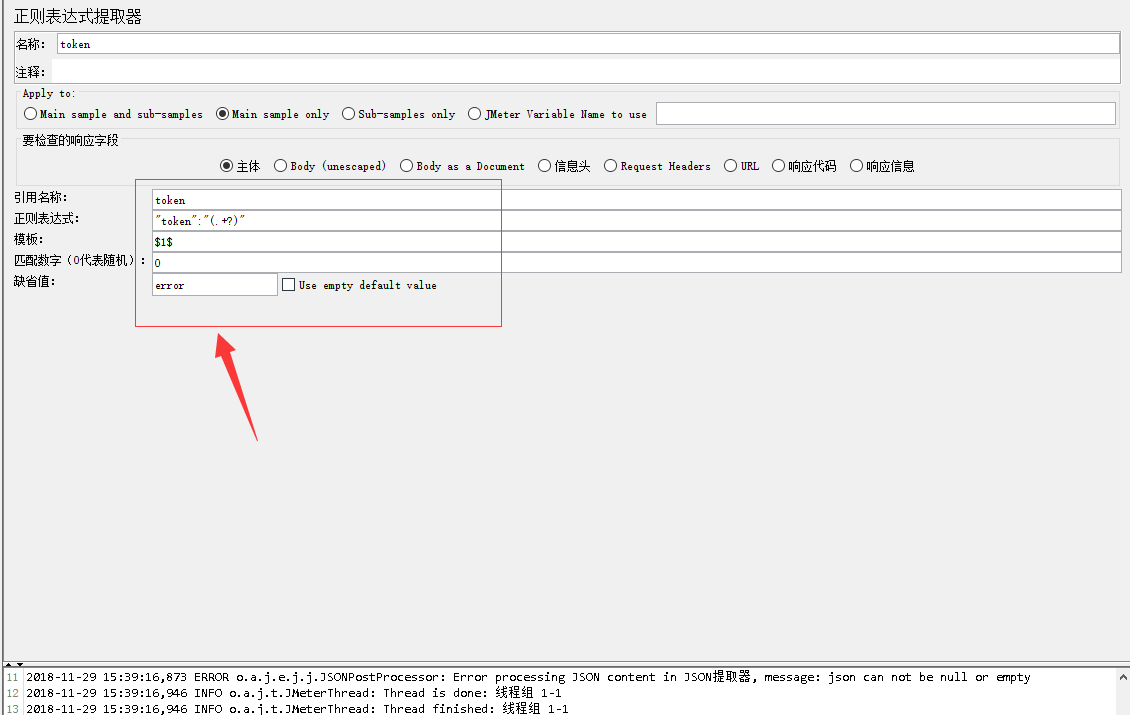
token正则表达式："token":"(.+?)"

模板：$1$

添加信息头管理器进行配置

需要token得地方输入 ${token}

就可以了

如果获取 返回值 只有数字得 且不带 ”“得

正则表达式："sysId":([0-9]*?),

校验正则表达式可通过 请求值 进行校验

欢迎关注老王公众号

jmeter正则表达式提取 引用的更多相关文章

  1. Jmeter正则表达式提取器的使用方法（转）

    下面简单介绍一下Jmeter正则表达式提取器的使用方法. 1.添加Jmeter正则表达式提取器:在具体的Request下添加Jmeter正则表达式提取器(Jmeter正则表达式在“后置处理器”下面)  ...

  2. JMeter 关于JMeter 正则表达式提取器的一点研究

    关于JMeter 正则表达式提取器的一点研究   by:授客 QQ:1033553122 1.   实验环境: JMeter 2.13 2.   添加正则表达式提取器 右键线程组->添加-> ...

  3. jmeter正则表达式提取器--关联

    http://desert3.iteye.com/blog/1394934 1.http://www.cnblogs.com/quange/archive/2010/06/11/1756260.htm ...

  4. Jmeter 正则表达式提取器详解（Regular Expression Exactor）

    Jmeter 正则表达式提取器详解(Regular Expression Exactor) Name(名称):随意设置,最好有业务意义. Comments(注释):随意设置,可以为空 Apply to ...

  5. jmeter正则表达式提取

    使用jmeter正则表达式提取器之前,首先 使用httpwatch 分析一下 我要要测试的系统正则管理的规则: 例如:我这里要关联的是一个ODS数据仓库平台的登录 1./sso/login..单点登录 ...

  6. 02、Jmeter正则表达式提取器

    转载自:http://blog.csdn.net/quiet_girl/article/details/50724313 在使用Jmeter过程中,会经常使用到正则表达式提取器提取器,虽然并不直接涉及 ...

  7. Jmeter正则表达式提取器（转载）

    转载自 http://blog.csdn.net/qq_35885203 使用jmeter来测试时,经常会碰到需要上下文传输数据的情况,如登录后生成的token,在其他页面的操作,都需传入这个toke ...

  8. jmeter 正则表达式提取器的使用（提取第一个匹配结果）

    原文地址https://www.cnblogs.com/xueli/p/7405258.html?utm_source=itdadao&utm_medium=referral 正则表达式的用处 ...

  9. Jmeter正则表达式提取器

    https://www.cnblogs.com/tudou-22/p/9566894.html Jmeter中关联是通过“添加—后置处理器—正则表达式提取器”来获取数据 一.获取单个数据

随机推荐

  1. JS随机生成100个DIV每10个换行(换色，生成V字和倒V)

    附图 <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8& ...

  2. Android商城开发系列（十二）—— 首页推荐布局实现

    首页新品推荐的布局效果如下图: 这块布局是使用LinearLayout和GridView去实现,新建recommend_item.xml,代码如下所示: <?xml version=" ...

  3. jq动态增加的button标签click回调失效的问题，即动态增加的button标签绑定事件$("button.class").click(function)无效

    对于新增加的页面元素,改变了页面结构,如果是使用老办法$("button.class").click(function)去监听新的button标签事件,会失效. 笔者的应用是文字的 ...

  4. hihocoder 1109 堆优化的Prim算法

    题目链接:http://hihocoder.com/problemset/problem/1109 , 最小生成树 + 堆优化(优先队列). 可以用优先队列,也可以自己手动模拟堆,为了练手,我两种都试 ...

  5. 浅谈前端性能优化（二）——对HTTP传输进行压缩

    1.前端性能优化的一点: 对js.css.图片等进行压缩,尽可能减小文件的大小,减少文件下载的时间,从而减少网页响应的时间. 2.前端性能优化的另一点: 对HTTP传输进行压缩,即在js,css.图片 ...

  6. 【BZOJ4001】[TJOI2015] 概率论（卡特兰数）

    点此看题面 大致题意: 问你一棵\(n\)个节点的有根二叉树叶节点的期望个数. 大致思路 看到期望,比较显然可以想到设\(num_i\)为\(i\)个节点的二叉树个数,\(tot_i\)为所有\(i\ ...

  7. 快速开发一个PHP扩展

    快速开发一个PHP扩展 作者:heiyeluren时间:2008-12-5博客:http://blog.csdn.net/heiyeshuwu 本文通过非常快速的方式讲解了如何制作一个PHP 5.2 ...

  8. STM32启动流程

    启动文件主要工作: . 设置堆栈指针SP=_initial_sp . 设置PC指针=Reset_Handler . 配置系统时钟 . 配置外部SRAM用于程序变量等数据存储(可选) . 调用C库中的_ ...

  9. vue中created、mounted等方法整理

  10. CUDA：Supercomputing for the Masses (用于大量数据的超级计算)-第六节

    原文链接 第六节:全局内存和CUDA RPOFILER  Rob Farber 是西北太平洋国家实验室(Pacific Northwest National Laboratory)的高级科研人员.他在 ...