2015 Dhaka

2015 Dhaka

A - Automatic Cheater Detection

solution
模拟计数。

B - Counting Weekend Days

solution
模拟计数。

C - Toll Management IV

题目描述：有一个\(n\)个点\(m\)条边的图，每条边有权值，现在给出图中一棵合法的最小生成树，问每条边权值最多增加多少，最多减少多少，使得给出的最小生成树还是最小生成树。

solution
对于给定的最小生成树，最多减少多少无界，对于其它的边，最多增加多少无界。
对于每一条非最小生成树上的边，最多减少的值为该边的两个端点在树上的路径的最大权值，而树上的路径权值最多增加到该边的边权。
因此可以用倍增的方法求出树的两点间的最大值，以及维护两点间的最多增加到的值。

时间复杂度：\(O(nlogn)\)

D - Owllen

solution
答案为出现次数最少的字母的出现次数。

E - Sum of MSLCM

题目描述：求\(1\)~\(n\)的约数的和的和。

solution
这显然是个积性函数，所以可用线性筛预处理。

时间复杂度：\(O(n)\)

F - Unique Party

题目描述：给定一个网格图，每个格子有一个值。现在有\(Q\)个询问，每次询问一个中位数(取大的那个)大于等于\(h\)的最大矩形面积。

solution
对于一个询问\(h\)，将网格中大于等于\(h\)的值变为\(1\)，将小于\(h\)的值变为\(-1\)，则原问题相当于是求子矩阵的和非负的最大子矩阵的面积。枚举子矩阵的第一行与最后一行，求出每一列在这段区间的和，二维问题变为一维问题，求前缀和\(sum\)，将区间的和变为两点的差，存在包含的区间只考虑长的那个即可，因此如果\(sum[i+1]>=sum[i]\)，则\(i\)不会成为右端点。枚举右端点，左端点单调。

时间复杂度：\(O(n^3)\)

G - Honey King

题目描述：在二维蜂巢中定义坐标，给定一些坐标，求包含这些坐标的最小正六边形里面的点数。

solution

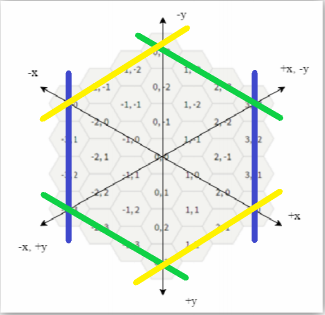
二分正六边形的边长（也可以说是正六边形的层数），如上图所示，如果以\((0, 0)\)作为中心点，那么蓝色是\(x\)坐标的界，绿色是\(y\)坐标的界，黄色是\(x+y\)的界，因此可以对每个坐标可以算出中心点的可行区间，然后判断每个坐标的可行区间的交是否有解即可。

时间复杂度：\(O(nlogn)\)

H - Design New Capital

题目描述:给定二维平面上的若干个坐标（不在坐标轴上），选择若干个坐标，使得原点是与所有选择的点的曼哈顿距离的和最小的解之一，问选择\(i\)个点的方案数。

solution
原题等价于选择的点的\(x\)坐标的中间两个数之间有\(0\)，\(y\)坐标也是。所以第一象限的点数要等于第三象限的点数，第二象限的点数要等于第四象限的点数，用组合数可以算出第一，第二象限选\(i\)个数的方案，然后用\(NTT\)求卷积即可。

时间复杂度：\(O(nlogn)\)

I - Numbered Cards

题目描述：有\(n\)个数\(1\)~\(n\)，问从中选择若干个数，使得任意两个数没有相同的数字的方案数。

solution
状压\(dp\)(集合\(dp\))+数位\(dp\)
状压\(dp\)记住当前用了哪些数字，枚举新的一个数用了哪些数字，然后这个新的数有多少个可以用数位\(dp\)来求。

时间复杂度：\(O(2^{10}*?*9*10)\)

J - The Hypnotic Spirals