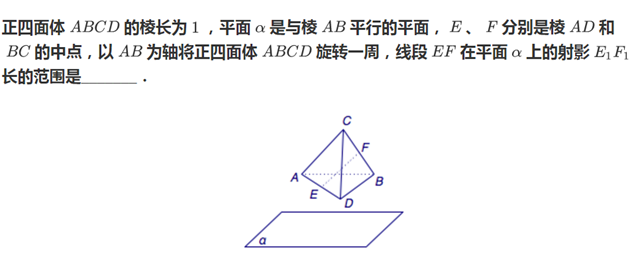
解：如图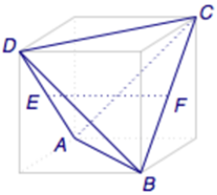将正四面体放到立方体中，让AB通过$\alpha$面，让$\alpha$面绕着AB动起来。问题就转化成为EF与面$\alpha$线面角$\theta$了。EF的投影为$|EF|cos\theta$.由于$<EF,AB>=\frac{\pi}{4}$故有线面角的最小性得$0\le\theta\le\frac{\pi}{4}$.从而得投影范围为$[\frac{1}{2},\frac{\sqrt{2}}{2}]$

评:线面角的最小性再求范围中可以结合固定的两条异面直线的角度判断范围.

MT【118】利用线面角最小解题的更多相关文章

  1. MT【108】线面角最小

    评:线面角最小,在此类最值中经常用到,作为选择填空可以投机.

  2. POJ 1061青蛙的约会。求解(x+mT)%L=(y+nT)%L的最小步数T。

    因为是同余,所以就是(x+mT)%L-(y+nT)%L=0.可以写成(x-y+(m-n)T)%L=0.就是这个数是L的倍数啦.那么我可以这样x-y+(m-n)T + Ls = 0.就可以了,s可正可负 ...

  3. 利用线上数据验证系统 Gor

    Web 应用性能和压力测试工具 Gor - 运维生存时间 http://hao.jobbole.com/gorhttp/ 要使用线上引流到测试环境的作用,需要做到以下几点: 1.新搭建一套测试环境,连 ...

  4. MT【223】二次函数最大最小

    若函数$f(x)=ax^2+20x+14(a>0)$对任意实数$t$,在闭区间$[t-1,t+1]$上总存在两实数$x_1,x_2$,使得$|f(x_1)-f(x_2)|\ge8$成立,则实数$ ...

  5. MT【305】丹德林双球

    如图.在正方体$ABCD-A_1B_1C_1D_1$中,点$M,N$分别是直线$CD,AB$上的动点,点$P$是$\Delta A_1C_1D_1$内的动点(不包括边界),记直线$DP$与$MN$所成 ...

  6. POJ 3273-Monthly Expense 求分组和的最小的最大值【二分答案】

    题目链接:http://poj.org/problem?id=3273 题目大意:给出一个有n个数据的数组,将其分为连续的m份,找到一种分法,是的m份中最大一份总和最小 解题思路: 直接在答案的区间内 ...

  7. MT【193】三面角的正余弦定理

    (原题为浙江名校新高考研究联盟2018届第三次联考选择压轴题) 在平面$\alpha$内,已知$AB\perp BC$,过直线$AB,BC$分别作平面$\beta,\gamma$,使得锐二面角$\al ...

  8. L011-oldboy-mysql-dba-lesson11

    L011-oldboy-mysql-dba-lesson11 [root@ab01 ~]# mysqladmin -i 1 -r status     #mysqladmin监控的命令 Uptime: ...

  9. 二模 （12）day2

    第一题: 题目大意: 有N颗糖,两个人轮流取,每次只能取质数颗,不能取的输.求先取者若必胜,最少需要多少步胜利.(N<=10000) 解题过程: 1.看到N的范围比较小,先打个素数表,然后dp即 ...

随机推荐

  1. 获取本地ip和获取公网ip

    import socket def get_local_ip(): ''' 获取本地ip地址 :return: ''' s = socket.socket(socket.AF_INET, socket ...

  2. [Unity Shader] 坐标变换与法线变换及Unity5新增加的内置函数

    学习第六章Unity内置函数时,由于之前使用mul矩阵乘法时的顺序与书中不一致,导致使用内置函数时出现光照效果不一样,因此引出以下两个问题: 1 什么时候使用3x3矩阵,什么时候使用4x4矩阵? 2 ...

  3. iFIERO - (一) 宇宙大战 SPACE BATTLE — 场景SCENE、SpriteKit精灵、PARTICLE粒子及背景音乐

    开始游戏教程前,首先介绍一下SpriteKit是什么?SpriteKit提供了一个图形渲染和动画的基础结构,你可以使用它让任意类型的纹理图片或者精灵动起来.SpriteKit使用渲染循环,利用图形硬件 ...

  4. Unity — — UGUI之背包物品拖放

    最新背包代码: Unity3D — — UGUI之简易背包 Unity版本:2017.3 功能:用UGUI实现简单的背包物品拖放/交换功能 一.简介 在UGUI下,物品的拖放脚本实现主要依赖于Unit ...

  5. Siki_Unity_3-6_UI框架 (基于UGUI)

    Unity 3-6 UI框架 (基于UGUI) 任务1&2&3&4:介绍 && 创建工程 UI框架: 管理场景中所有UI面板 控制面板之间的跳转 如果没有UI框 ...

  6. Jmeter实战

    Jmeter实战 入门篇 1.下载与使用 下载地址:http://jmeter.apache.org/download_jmeter.cgi 开源,基于java编写,所以得有jdk(jre)环境,下载 ...

  7. python-GUI之tkinter的学习

    最近看了哔哩哔哩的python的学习,直接看代码吧,以后会更新 先来个基础的 import tkinter as tk #导入包 app = tk.Tk() #抽象出一个GUI app.title(& ...

  8. 【坚持】Selenium+Python学习之从读懂代码开始 DAY4

    2018/05/21 [生成器详解:廖雪峰的官方网站](https://www.liaoxuefeng.com/wiki/0014316089557264a6b348958f449949df42a6d ...

  9. 拒绝滥用golang defer机制

    原文链接 : http://www.bugclosed.com/post/17 defer机制 go语言中的defer提供了在函数返回前执行操作的机制,在需要资源回收的场景非常方便易用(比如文件关闭, ...

  10. DDMS_Threads的简单使用

    title: DDMS_Threads的简单使用 date: 2016-07-20 00:44:35 tags: [DDMS] categories: [Tool,IDE] --- 概述 本文记录在 ...