【BZOJ4800】[CEOI2015 Day2]世界冰球锦标赛 （折半搜索）

[CEOI2015 Day2]世界冰球锦标赛

题目描述

译自 CEOI2015 Day2 T1「Ice Hockey World Championship」

今年的世界冰球锦标赛在捷克举行。\(Bobek\) 已经抵达布拉格，他不是任何团队的粉丝，也没有时间观念。他只是单纯的想去看几场比赛。如果他有足够的钱，他会去看所有的比赛。不幸的是，他的财产十分有限，他决定把所有财产都用来买门票。

给出 \(Bobek\) 的预算和每场比赛的票价，试求：如果总票价不超过预算，他有多少种观赛方案。如果存在以其中一种方案观看某场比赛而另一种方案不观看，则认为这两种方案不同。

输入输出格式

输入格式：

第一行，两个正整数 \(N\) 和 \(M(1 \leq N \leq 40,1 \leq M \leq 10^{18})\)，表示比赛的个数和 \(Bobek\) 那家徒四壁的财产。

第二行，\(N\) 个以空格分隔的正整数，均不超过 \(10^{16}\)，代表每场比赛门票的价格。

输出格式：

输出一行，表示方案的个数。由于 \(N\) 十分大，注意：答案 \(\le 2^{40}\)。

输入输出样例

输入样例#1：

5 1000
100 1500 500 500 1000

输出样例#1：

8

说明

样例解释

八种方案分别是：

• 一场都不看，溜了溜了
• 价格 \(100\) 的比赛
• 第一场价格 \(500\) 的比赛
• 第二场价格 \(500\) 的比赛
• 价格 \(100\) 的比赛和第一场价格 \(500\) 的比赛
• 价格 \(100\) 的比赛和第二场价格 \(500\) 的比赛
• 两场价格 \(500\) 的比赛
• 价格 \(1000\) 的比赛

有十组数据，每通过一组数据你可以获得 \(10\) 分。各组数据的数据范围如下表所示：

数据组号	1-2	3-4	5-7	8-10
$N \leq $	\(10\)	\(20\)	\(40\)	\(40\)
\(M \leq\)	\(10^6\)	\(10^{18}\)	\(10^6\)	\(10^{18}\)

题解

首先看数据范围

1. 1-4组数据\(N\leq20\)，爆搜就可以解决。

   inline void dfs(R ll dep,R ll sum){
   	if(sum>m)return;
   	if(dep==n+1){
   		ans++;
   		return;
   	}
   	dfs(dep+1,sum+a[dep]);
   	dfs(dep+1,sum);
   }
   int main(){
   	read(n);read(m);
   	for(R int i=1;i<=n;i++)read(a[i]);
   	if(n<=20){
   		dfs(1,0);
   		printf("%lld\n",ans);
   	}
       return 0;
   }
   

2. 5-7组数据\(M\leq10^6\)，裸的背包啊。

   int main(){
   	read(n);read(m);
   	for(R int i=1;i<=n;i++)read(a[i]);
       if(m<=1e6){
           f[0]=1;
           for(R int i=1;i<=n;i++)
               for(R int j=m;j>=a[i];j--)
                   f[j]+=f[j-a[i]];
           for(R int i=0;i<=m;i++)ans+=f[i];
           printf("%lld\n",ans);
       }
       return 0;
   }
   
   

3. 现在你已经能拿到70分了（但在洛谷上是47分）

下面引出主角——折半搜索（meet in the middle思想）

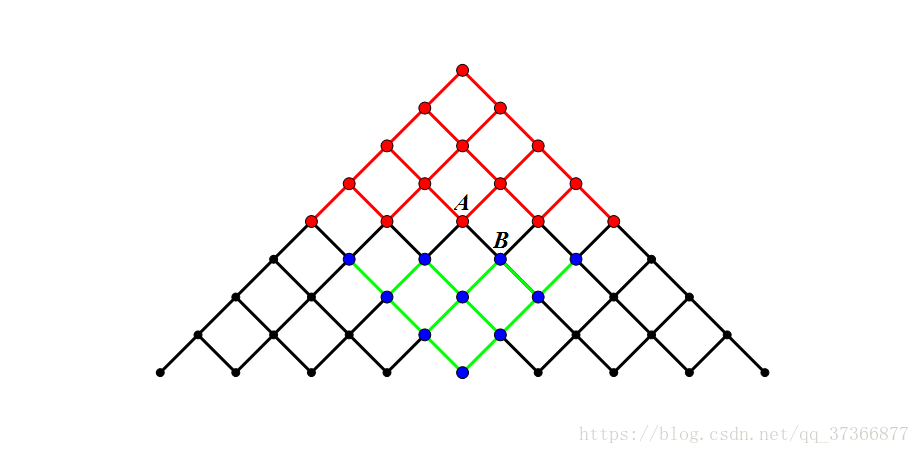
因为\(N\leq40\) \(O(2^{40})\)的爆搜一定会\(TLE\)，所以我们将\(N\)分成两份

搜索\(1\)到\(n/2\)和\(n/2+1\)到\(n\)，让复杂度降到\(O(2^{n/2+1})\)。

画一个图（网上找的不错的图）理解一下为什么能降低复杂度

inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
    if(sum>m)return;
    if(l>r){
        a[++cnt]=sum;
        return;
    }
    dfs(l+1,r,sum+w[l],a,cnt);//选
    dfs(l+1,r,sum,a,cnt);//不选
}

将前一半的搜索状态存入a数组，后一半存入b数组。

mid=n/2;
dfs(1,mid,0,suma,cnta);
dfs(mid+1,n,0,sumb,cntb);

一般\(meet\) \(in\) \(the\) \(middle\)的难点主要在于最后答案的组合统计。

我们可以现将a或b数组sort，让其有序。

然后通过枚举另一个数组中的状态，来实现统计答案。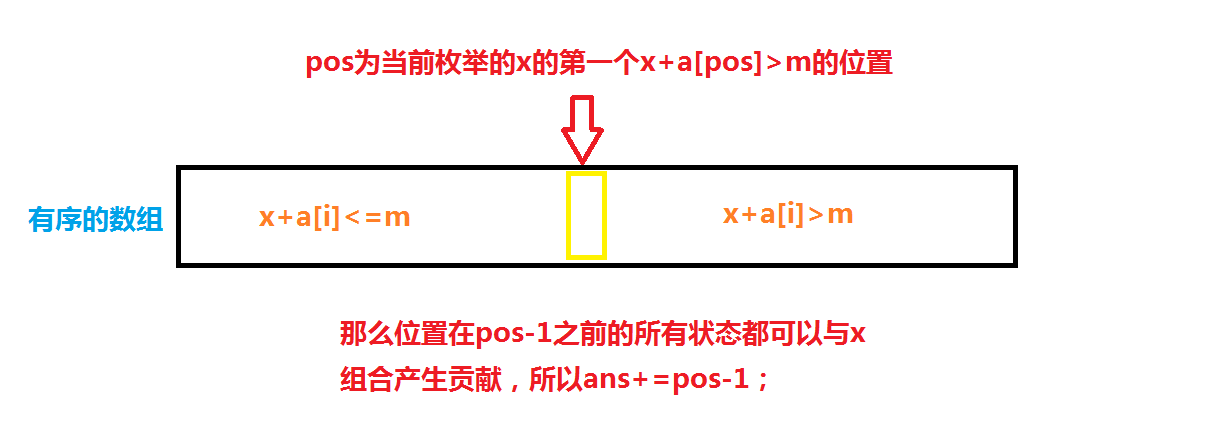

上述找\(pos\)的过程可以通过upper_bound()完成。

sort(suma+1,suma+1+cnta);//使一个数组有序
for(R int i=1;i<=cntb;i++)
    ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;//统计ans

下面是高清完整code：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cctype>
#define ll long long
#define R register
#define N 55
using namespace std;
template<typename T>inline void read(T &a){
    char c=getchar();T x=0,f=1;
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    a=f*x;
}
ll n,m,w[N],mid,suma[1<<21],sumb[1<<21],cnta,cntb,ans;
inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
    if(sum>m)return;
    if(l>r){
        a[++cnt]=sum;
        return;
    }
    dfs(l+1,r,sum+w[l],a,cnt);
    dfs(l+1,r,sum,a,cnt);
}
int main(){
    read(n);read(m);
    for(R int i=1;i<=n;i++)read(w[i]);
    mid=n>>1;
    dfs(1,mid,0,suma,cnta);
    dfs(mid+1,n,0,sumb,cntb);
    sort(suma+1,suma+1+cnta);
    for(R int i=1;i<=cntb;i++)
        ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;
    printf("%lld\n",ans);
    return 0;
}

这里还有一道折半搜索的好题，难度升级——luogu，还有 my blog.