Codefores 507D The Maths Lecture( 数位DP )

D. The Maths Lecture

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Amr doesn't like Maths as he finds it really boring, so he usually sleeps in Maths lectures. But one day the teacher suspected that Amr is sleeping and asked him a question to make sure he wasn't.

First he gave Amr two positive integers n and k. Then he asked Amr, how many integer numbers x > 0 exist such that:

• Decimal representation of x (without leading zeroes) consists of exactly n digits;
• There exists some integer y > 0 such that:
  • ;
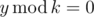  • decimal representation of y is a suffix of decimal representation of x.

As the answer to this question may be pretty huge the teacher asked Amr to output only its remainder modulo a number m.

Can you help Amr escape this embarrassing situation?

Input

Input consists of three integers n, k, m (1 ≤ n ≤ 1000, 1 ≤ k ≤ 100, 1 ≤ m ≤ 10⁹).

Output

Print the required number modulo m.

Sample test(s)

Input

1 2 1000

Output

4

Input

2 2 1000

Output

45

Input

5 3 1103

Output

590

Note

A suffix of a string S is a non-empty string that can be obtained by removing some number (possibly, zero) of first characters from S.

题意是统计n位数x , 它有一个后缀y，能够满足（ y%k==0）的 x 的个数.我做法是开一个3维数组 ， dp[i][j][y] 。 表示符合前 i 位 ， 余数是j， 是否有前导 0 的数的个数。

首先要预处理了 i*j^10 % k 的结果，（ i = 1~9 , j = 1~n ）用于对新的状态的转移。

预处理好排列数 10^j % m ，当出现后缀y符合条件且没前导0 ,可进行计算。

剩下就是状态转移了 。

转移的过程中 无前导0 且 余数等于0 的可以进行一次计数。

否则就继续进行转移就OK 。

代码写得比较恶心...然后要注意处理好边界就没什么问题了。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N =  ;
const int M =  ;
LL dp[N][M][] , n , m , k , cnt[N] , rest[][N];

void init() {
    cnt[] =  ;
    for( int i =  ; i <= n ; ++i ) {
        cnt[i] = cnt[i-] *  % m ;
    }
    for( int j =  ; j <= n ; ++j ) {
        for( int i =  ; i <  ; ++i ) {
            if( j ==  ) rest[i][j] = i % k ;
            else rest[i][j] = (  % k * rest[i][j-] ) % k ;
//            cout << i << ' ' << j << ' ' << rest[i][j] << endl ;
        }
    }
    memset( dp ,  , sizeof dp );
    for( int i =  ; i <  ; ++i ) dp[][i%k][!i]++;
//    cout << "Run" << endl ;
}

void Run() {
    LL ans =  ;
    if( n ==  ) {
        for( int i =  ; i <  ; ++i ) if( i % k ==  ) ans ++ , ans %= m;
    }
    else {
        for( int i =  ; i <= n ; ++i ) {
            for( int j =  ; j < k ; ++j ) {
                for( int y =  ; y <  ; ++y ) {
                    if( !y && !j ) {             // no leading zero and reminder equal zero
                        if( i < n ) ans = ( ans +  * cnt[n-i-] % m * dp[i][j][y] ) % m ;
                        else ans += dp[i][j][y] , ans %= m ;
                    }
                    else {                      // leading zero or reminder not equal zero
                        for( int z =  ; z <  ; ++z ) {
                            int i1 = i +  , j1 = ( rest[z][i1] + j ) % k ;
                            dp[i1][j1][!z] += dp[i][j][y] , dp[i1][j1][!z] %= m ;
                        }
                    }
                }
            }
        }
    }
    cout << ans << endl ;
}
int main()
{
//    freopen("in.txt","r",stdin);
    while( cin >> n >> k >> m )
        init() , Run();
}