剑指offer第二版面试题6：重建二叉树（JAVA版）

题目：输入某二叉树的前序遍历和中序遍历的结果，请重新构造出该二叉树。假设输入的前序遍历和中序遍历的结果中不包含重复的数字。例如输入的前序遍历序列为｛1，2，4，7，3，5，6，8｝和中序遍历为{4,7,2,1,5,3,6,8},则重建出二叉树并输出它的头结点。

前序遍历：根节点--》左节点--》右节点

中序遍历：左节点--》根节点--》右节点

后序遍历：左节点--》右节点--》根节点

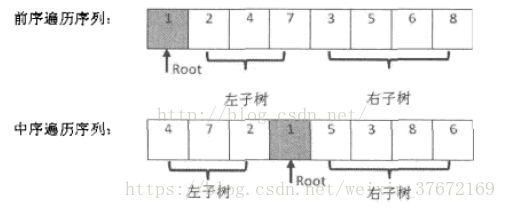
在二叉树的前序遍历序列中，第一个数字总是树的根节点的值。但在中序遍历中，根节点的值在序列的中间，左子树的结点的值位于根节点的值的左边，而右子树的结点的值位于根节点的右边。因此我们需要扫描中序遍历序列，才能找到根节点的值。

如图所示，前序遍历序列的第一个数字1就是根节点的值。扫描中序遍历序列，就能确定根节点的值的位置。根据中序遍历的特点，在根节点的值1前面3个数字都是左子树结点的值，位于1后面的数字都是右子树结点的值。

由于中序遍历序列中，有3个数字是左子树结点的值，因此左子树总共有3个左子结点。同样，在前序遍历的序列中，根节点后面的3个数字就是3个左子树结点的值，再后面的所有数字都是右子树结点的值。这样我们就在前序遍历和中序遍历两个序列中，分别找到了左右子树对应的子序列。

然后再根据左子树的前序遍历和中序遍历找出根节点和左右子树，可以使用递归来完成,每次得到根节点

用左子树来举例：

第二次：

前序：247

中序：472

根节点2，由中序可知没有右节点

第三次：

前序：47

中序：47

根节点：4

没有了左子树，7为4的右节点

代码如下：

/**
 * 树节点
 */
class BinaryTreeNode {
    int value;
    BinaryTreeNode leftNode;
    BinaryTreeNode rightNode;
    public BinaryTreeNode(int value){
        this.value=value;
    }
    public int getValue() {
        return value;
    }
    public void setValue(int value) {
        this.value = value;
    }
    public BinaryTreeNode getLeftNode() {
        return leftNode;
    }
    public void setLeftNode(BinaryTreeNode leftNode) {
        this.leftNode = leftNode;
    }
    public BinaryTreeNode getRightNode() {
        return rightNode;
    }
    public void setRightNode(BinaryTreeNode rightNode) {
        this.rightNode = rightNode;
    }

}

public class RebuildTree {
    /**
     * 根据前序遍历和中序遍历重建二叉树
     * */
    public static BinaryTreeNode rebuildTree(int[] preOrder, int[] inOrder){
        if (preOrder == null || inOrder == null || preOrder.length == 0 || inOrder.length == 0 || preOrder.length != inOrder.length) {
            return null;
        }
        //根节点
        BinaryTreeNode root=new BinaryTreeNode(preOrder[0]);
        root.setLeftNode(null);
        root.setRightNode(null);
        //左子树节点的个数
        int leftNum=0;
        for(int i=0;i<inOrder.length;i++){
            if(inOrder[i]==root.getValue()){
                break;
            }else{
                leftNum++;
            }
        }
        //右子树节点的个数
        int rightNum=inOrder.length-1-leftNum;

        //重建左子树
        while(leftNum>0){
            //用来存放左子树的前序遍历
            int leftPreOrder[]=new int[leftNum];
            //用来存放左子树的中序遍历
            int leftInOrder[]=new int[leftNum];
            //赋值给左子树每个节点值，把左子树再独立成一棵树
            for(int i=0;i<leftNum;i++){
                leftPreOrder[i]=preOrder[i+1];
                leftInOrder[i]=inOrder[i];
            }
            BinaryTreeNode leftRoot=rebuildTree(leftPreOrder, leftInOrder);
            root.setLeftNode(leftRoot);
        }
        //重建右子树
        while(rightNum>0){
            //右子树的前序遍历
            int rightPreOrder[]=new int[rightNum];
            //右子树的中序遍历
            int rightInOrder[]=new int[rightNum];
            //赋值

            for(int i=0;i<rightNum;i++){
                rightPreOrder[i]=preOrder[i+1+leftNum];
                rightInOrder[i]=preOrder[i+1+leftNum];
            }
            BinaryTreeNode rightNode=rebuildTree(rightPreOrder, rightInOrder);
            root.setRightNode(rightNode);
        }

        return root;
    }

    public static void main(String[] args) {
        // 二叉树的先序序列
        int[] preOrder = { 1, 2, 4, 7, 3, 5, 6, 8 };
        // 二叉树的中序序列
        int[] inOrder = { 4, 7, 2, 1, 5, 3, 8, 6 };
        BinaryTreeNode root = rebuildTree(preOrder, inOrder);
    }
}