【CF1255A】Changing Volume【思维】

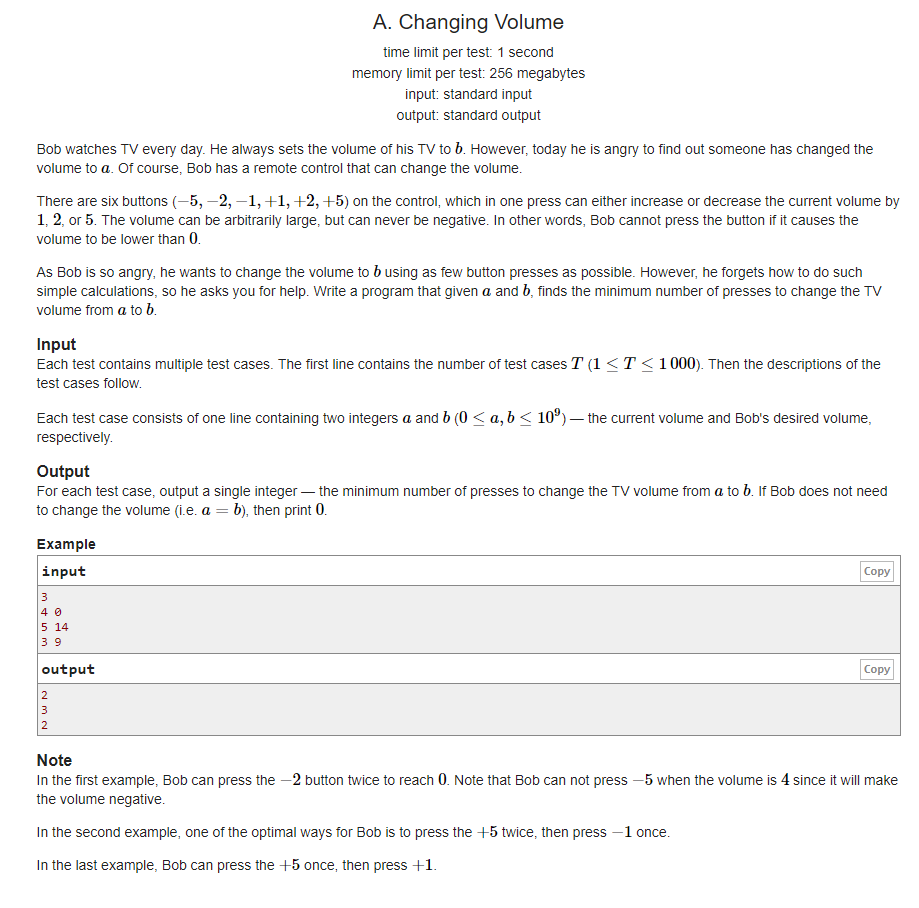
题意：每次可以-5/-2/-1/+1/+2/+5，问是否存在方案使得A变成B

题解：首先我们可以设A<B，若A>B，则交换AB，因为A到B和B到A是互逆的过程，所以可以交换

其次将B-=A，因为从3到5和从0到2是一样的

这样题目转化为每次可以-5/-2/-1/+1/+2/+5，问是否存在方案总和为B

若一种方案同时存在加法和减法，那么相互抵消之后，同一个数只存在加法或减法，即-5+1+2是合法的，而-5+1+2+5不是，因为没有抵消完

观察经过次数可以达到的数

一：1 2 5

二：1 2 3 4 5 6 7 10

三：1 2 3 4 5 6 7 8 9 10 11 12 15

容易看出如果B为1/2/5则一次即可达到

如果B为5的倍数，则B/5次可以达到

否则设次数为i，则需要满足(i-1)*5+2>=B且(i-2)*5+2<B

容易解出i=(B-3)/5+2

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
int T;
int a,b;
int main()
{
    scanf("%d",&T);
    while(T--)
    {
      scanf("%d%d",&a,&b);
      if(a>b)swap(a,b);
      b-=a;
      if(b== || b== || b==)printf("1\n");
      else
      {
        if(b%==)printf("%d\n",b/);
        else printf("%d\n",(b-)/+);
      }
    }
    return ;
}