P1076 寻宝

P1076 寻宝

题解

这道题真是感人啊，废了蒟蒻一天的时间

关键

1.

a[ k ][ ] 数组记录第k层有楼梯房间的编号

a[ k ][ 0 ]  第k层有几个有楼梯的房间

a[ k ][ i ] 第k层第 i 个有楼梯的房间

每层记录每一个房间的下一个有楼梯的房间，在后面牵扯到 x 的运算时会用到

也就是

2.这里讲一下 x 的处理：

因为 x 可能会很大，所以要处理一下，防止没用的跑很多圈，

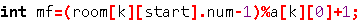
简化为 (x-1)%y+1 

如果 x%y=0的话，酱紫就会得到正确的结果（非0）

如果 x%y!=0的话，结果还是 x%y 啊

为什么要%y再+1呢？

其实就是相当于把取模后的值从 0,1,2,3,.....,y-1，变成了 1,2,3,4,.....,y，也就是不会出现0

为什么要（x-1）呢??

如果不先 -1 ，后面+1之后结果就不一样了

for example：

（10-1）%3+1=10%3=1

这里加上一个题目  也是运用了一下这样的处理方法：

P2615 神奇的幻方

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,x,y;
int tu[][];

int main()
{
//    freopen("data.txt","r",stdin);
//    freopen("yy.txt","w",stdout);

    n=read();
    x=;y=(n+)/;
    tu[x][y]=;

    for(int i=;i<=n*n;i++)
    {
        int xx,yy;
        xx=((x-)-+n)%n+;
        yy=((y+)-+n)%n+;
    //    xx=x-1;if(xx<1) xx=n;
    //    yy=y+1;if(yy>n) yy=1;
        if(!tu[xx][yy]){
            tu[xx][yy]=i;
            x=xx;y=yy;
            continue;
        }
        else{
            xx=((x+)-+n)%n+;
        //    xx=x+1;if(xx>n) xx=1;
            yy=y;
            tu[xx][yy]=i;
            x=xx;y=yy;
        }
    }

    for(int i=;i<=n;i++){
        for(int j=;j<=n;j++)
          printf("%d ",tu[i][j]);
        printf("\n");
    }

    return ;
}

Code

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>

using namespace std;

const int mod=;
int n,m,start,ans,b,c;
int a[][];
struct node
{
    int num;
    int flag;
    int next;
}room[][];

int main()
{
    memset(a,-,sizeof(a));
    scanf("%d%d",&n,&m);

    for(int i=;i<=n;i++)
    {
        a[i][]=;     //初始化记录每层有几个楼梯
        int ge=;        //每层楼梯个数，初始化0
        for(int j=;j<m;j++)
        {
            scanf("%d%d",&room[i][j].flag,&room[i][j].num);
            room[i][j].next =-;
            if(room[i][j].flag )
            {
                a[i][]++;
                a[i][++ge]=j;   //第i层第ge个有楼梯的房间编号为j
          }
        }
    }
    scanf("%d",&start);

    //记录每个房间下一个有楼梯房间的编号
    for(int i=;i<=n;i++)
    {
        int ge=;
        for(int j=;j<m;j++)
        {
            if(room[i][j].flag )    ge++;

            if(ge==a[i][]) room[i][j].next =a[i][];  //最后一个和第一个连起来
            else room[i][j].next =a[i][ge+];
        }
    }

    for(int i=;i<=n;i++)
    {
        ans=(ans+room[i][start].num )%mod;

        int mp=(room[i][start].num-1)%a[i][0]+1;  //看关键2 

        int tim=;
        if(room[i][start].flag) tim++;

        while(tim<mp)
        {
            start=room[i][start].next;
            tim++;
        }

    }

    printf("%d\n",ans);

    return ;
}